Алгоритм Краскала

Алгоритм Краскала (англ. Kruskal's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе.

Идея

Будем последовательно строить подграф [math]F[/math] графа [math]G[/math] ("растущий лес"), поддерживая следующий инвариант: на каждом шаге [math]F[/math] можно достроить до некоторого MST. Начнем с того, что включим в [math]F[/math] все вершины графа [math]G[/math]. Теперь будем обходить множество [math]EG[/math] в порядке увеличения веса ребер. Добавление очередного ребра [math]e[/math] в [math]F[/math] может привести к возникновению цикла в одной из компонент связности [math]F[/math]. В этом случае, очевидно, [math]e[/math] не может быть включено в [math]F[/math]. В противном случае [math]e[/math] соединяет разные компоненты связности [math]F[/math], тогда существует разрез [math] \langle S, T \rangle [/math] такой, что одна из компонент связности составляет одну его часть, а оставшаяся часть графа - вторую. Тогда [math]e[/math] и есть минимальное ребро, пересекающее этот разрез. Значит, из леммы о безопасном ребре следует, что [math]F+e[/math] можно продолжить до MST, поэтому добавим это ребро в [math]F[/math].

Реализация

// [math]G[/math] — исходный граф
// [math]F[/math] — минимальный остов
function [math]\mathtt{kruskalFindMST}():[/math]
   [math] \mathtt{F}\ =\ \varnothing [/math]
   for [math]v \in V(G)[/math]
      [math]\mathtt{makeSet}(v)\[/math]
   [math]\mathtt{sort}(E(G))\[/math]
   for [math]vu \in E(G)[/math]
      if [math]\mathtt{findSet}(v)\ \ne \mathtt{findSet}(u)[/math]
         [math] \mathtt{F}\ =\ \mathtt{F} \bigcup \mathtt{vu}\[/math]
         [math]\mathtt{Unite}(v, u)\ [/math]

Задача о максимальном ребре минимального веса

Очевидно, что максимальное ребро в MST минимально. Пусть это не так, тогда рассмотрим разрез, который оно пересекает. В этом разрезе должно быть ребро с меньшим весом, иначе максимальное ребро было бы минимальным, но в таком случае минимальный остов не является минимальным, следовательно, максимальное ребро в минимальном остовном дереве минимально. Если же максимальное ребро в остовном дереве минимально, то такое дерево может не быть минимальным. Зато его можно найти быстрее чем MST, а конкретно за [math]O(E)[/math]. Для этого с помощью алгоритма поиска k-ой порядковой статистики найдем за [math]O(E)[/math] ребро-медиану и разделим множество ребер на два подмножества, так чтобы в первом подмножестве ребра были меньше медианы, а во втором больше. Проверим образуют ли ребра из первого подмножества остов, просто сделав конденсацию за [math]O(E)[/math]. Если да, то рекурсивно найдем ответ для данного подмножества, иначе рассмотрим граф из скондесированных компонент и оставшихся ребер. На каждой итерации остается половина ребер, следовательно, время работы алгоритма [math]O(E+\frac{E}{2}+\frac{E}{4}+...+1)=O(E)[/math], так как [math]\sum\limits_{i=1}^n\frac{1}{2^i} = 1[/math].

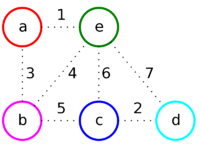
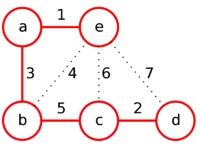
Пример

Задан неориентированный связный граф, требуется построить в нём минимальное остовное дерево.
Создадим новый граф, содержащий все вершины из заданного графа, но не содержащий рёбер.
Этот новый граф будет ответом, в него будут добавлены рёбра из заданного графа по ходу выполнения алгоритма.
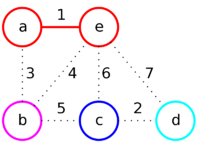
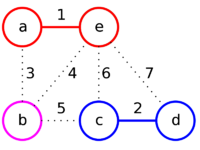
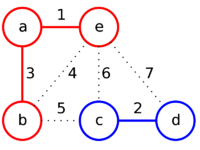
Отсортируем рёбра заданного графа по их весам и рассмотрим их в порядке возрастания.

Рёбра (в порядке их просмотра)	ae	cd	ab	be	bc	ec	ed
Веса рёбер	[math]1[/math]	[math]2[/math]	[math]3[/math]	[math]4[/math]	[math]5[/math]	[math]6[/math]	[math]7[/math]

Изображение	Описание
	Первое ребро, которое будет рассмотрено — ae, так как его вес минимальный. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (a — красное и e — зелёное). Объединим красное и зелёное множество в одно (красное), так как теперь они соединены ребром.
	Рассмотрим следующие ребро — cd. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (c — синее и d — голубое). Объединим синее и голубое множество в одно (синее), так как теперь они соединены ребром.
	Дальше рассмотрим ребро ab. Добавим его к ответу, так как его концы соединяют вершины из разных множеств (a — красное и b — розовое). Объединим красное и розовое множество в одно (красное), так как теперь они соединены ребром.
	Рассмотрим следующие ребро — be. Оно соединяет вершины из одного множества, поэтому перейдём к следующему ребру bc Добавим его к ответу, так как его концы соединяют вершины из разных множеств (b — красное и c — синее). Объединим красное и синее множество в одно (красное), так как теперь они соединены ребром.
	Рёбра ec и ed соединяют вершины из одного множества, поэтому после их просмотра они не будут добавлены в ответ Всё рёбра были рассмотрены, поэтому алгоритм завершает работу. Полученный граф — минимальное остовное дерево

Асимптотика

Сортировка [math]E[/math] займет [math]O(E\log E)[/math].
Работа с DSU займет [math]O(E\alpha(V))[/math], где [math]\alpha[/math] - обратная функция Аккермана, которая не превосходит 4 во всех практических приложениях и которую можно принять за константу.
Алгоритм работает за [math]O(E(\log E+\alpha(V))) = O(E\log E) = O(E\log V^2) = O(E\log V)[/math].

См. также

• Алгоритм Прима
• Алгоритм Борувки

Источники информации

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ, 2-е издание. Пер. с англ. — М.:Издательский дом "Вильямс", 2010. — 1296 с.: ил. — Парал. тит. англ. — ISBN 978-5-8459-0857-5 (рус.)
• Википедия — Функция Аккермана
• Википедия — Алгоритм Крускала
• Wikipedia — Kruskal's algorithm
• MAXimal :: algo :: Минимальное остовное дерево. Алгоритм Крускала