Контексты и синтаксические моноиды — различия между версиями
Martoon (обсуждение | вклад) м (→Двухсторонний контекст) |
Martoon (обсуждение | вклад) |
||
| Строка 14: | Строка 14: | ||
<br/> | <br/> | ||
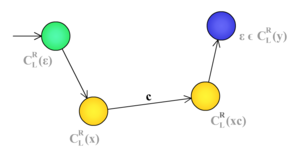
Пусть множество правых контекстов языка конечно. Построим распознающий его автомат. Состояния автомата будут соответствовать различным правым контекстам. Таким образом, каждая вершина автомата соответствует множеству допустимых «продолжений» считанного на данный момент слова. Переход по некоторому символу из одного состояния в другое осуществляется, если контекст, соответствующий первому состоянию, содержит все элементы, которые получаются приписыванием этого символа в начало элементам контекста, соответствующего второму. Вершина, соответствующая контексту пустого слова, является стартовой (<tex>C_L^R(\varepsilon) = L</tex>). Вершины, контексты которых содержат <tex>\varepsilon</tex>, должны быть допускающими. | Пусть множество правых контекстов языка конечно. Построим распознающий его автомат. Состояния автомата будут соответствовать различным правым контекстам. Таким образом, каждая вершина автомата соответствует множеству допустимых «продолжений» считанного на данный момент слова. Переход по некоторому символу из одного состояния в другое осуществляется, если контекст, соответствующий первому состоянию, содержит все элементы, которые получаются приписыванием этого символа в начало элементам контекста, соответствующего второму. Вершина, соответствующая контексту пустого слова, является стартовой (<tex>C_L^R(\varepsilon) = L</tex>). Вершины, контексты которых содержат <tex>\varepsilon</tex>, должны быть допускающими. | ||
| + | |||
| + | Покажем что полученный автомат допускает в точности указанный язык. По построению выполняется | ||
| + | : 1. <tex> u \leftrightarrow C_L^R(x) ,\ v \leftrightarrow C_L^R(xc) \quad \Leftrightarrow \quad \langle u,c \rangle \vdash \langle v, \varepsilon \rangle </tex> | ||
| + | : 2. <tex> s \leftrightarrow C_L^R(\varepsilon) </tex>, где <tex> s </tex> {{---}} стартовое состояние. | ||
| + | : 3. <tex> \varepsilon \in C_L^R(\omega) \Leftrightarrow v \in T \quad ( v \leftrightarrow C_L^R(\omega) ) </tex> | ||
| + | Из 1 следует | ||
| + | : 1*. <tex> u \leftrightarrow C_L^R(x) ,\ v \leftrightarrow C_L^R(x \omega) \quad \Leftrightarrow \quad \langle u,\omega \rangle \vdash^* \langle v, \varepsilon \rangle </tex> | ||
| + | Положив <tex> s = u </tex> и учтя 2, получим | ||
| + | * <tex> v \leftrightarrow C_L^R(\omega) \Leftrightarrow \langle s,\omega \rangle \vdash^* \langle v, \varepsilon \rangle </tex> | ||
| + | В таких условиях (мы фиксируем за состоянием <tex> v </tex> контекст <tex> C_L^R(\omega) </tex>) левая часть 3 равносильна <tex> \omega \in L </tex>, а правая означает, что автомат допускает <tex> \omega </tex>. | ||
<tex>\Rightarrow</tex> | <tex>\Rightarrow</tex> | ||
| Строка 36: | Строка 46: | ||
#: Начальное состояние {{---}} 1 (<tex> C_L^R(\varepsilon) </tex> рассматривалось в нём). | #: Начальное состояние {{---}} 1 (<tex> C_L^R(\varepsilon) </tex> рассматривалось в нём). | ||
#: Допускающие состояния: 4, 7, 9 (в них <tex> \varepsilon \in C_L^R(...) </tex>). | #: Допускающие состояния: 4, 7, 9 (в них <tex> \varepsilon \in C_L^R(...) </tex>). | ||
| − | #: Состояние 10 - [[Детерминированные_конечные_автоматы#допускает| | + | #: Состояние 10 {{---}} [[Детерминированные_конечные_автоматы#допускает|дьявольское]]. |
# <tex> 0^*11 </tex> | # <tex> 0^*11 </tex> | ||
#: Возможные правые контексты (аргументы упорядочены в лексикографическом порядке): | #: Возможные правые контексты (аргументы упорядочены в лексикографическом порядке): | ||
| Строка 44: | Строка 54: | ||
#:# <tex> C_L^R(0^*11) = \varepsilon </tex> | #:# <tex> C_L^R(0^*11) = \varepsilon </tex> | ||
#:# <tex> C_L^R(0^*11(0|1)^+) = \varnothing </tex> | #:# <tex> C_L^R(0^*11(0|1)^+) = \varnothing </tex> | ||
| − | #: Итого 4 состояния; начальное состояние 1, допускающее 4, состояние 3&5 {{---}} | + | #: Итого 4 состояния; начальное состояние 1, допускающее 4, состояние 3&5 {{---}} дьявольское. |
=== Левый контекст === | === Левый контекст === | ||
| Строка 64: | Строка 74: | ||
'''Двухсторонним контекстом''' (англ. ''two-sided context'') <tex>C_L(y)</tex> слова <tex>y</tex> в языке <tex>L</tex> называется множество <tex>\{\langle x,z\rangle \mid xyz \in L\}</tex>. | '''Двухсторонним контекстом''' (англ. ''two-sided context'') <tex>C_L(y)</tex> слова <tex>y</tex> в языке <tex>L</tex> называется множество <tex>\{\langle x,z\rangle \mid xyz \in L\}</tex>. | ||
}} | }} | ||
| − | ''' | + | '''Любопытное замечание:''' <tex>C_L(\varepsilon)</tex> состоит из всех пар строк, которые при конкатенации дают слово из языка. |
| Строка 76: | Строка 86: | ||
<br />Заметим, что <tex> \{ z \mid \langle \varepsilon, z \rangle \in C_L(y) \} = C_L^R(y) </tex>. Тогда если множество двухсторонних контекстов языка конечно, то конечно и множество его правых контекстов, а это значит, что язык регулярный. | <br />Заметим, что <tex> \{ z \mid \langle \varepsilon, z \rangle \in C_L(y) \} = C_L^R(y) </tex>. Тогда если множество двухсторонних контекстов языка конечно, то конечно и множество его правых контекстов, а это значит, что язык регулярный. | ||
<br /><tex>\Rightarrow</tex> | <br /><tex>\Rightarrow</tex> | ||
| − | Пусть <tex>L</tex> {{---}} регулярный. Тогда существует автомат <tex>\mathcal{A}</tex>, распознающий его. Понятно, что для любого слова <tex> xyz </tex>, допускаемого автоматом, существуют <tex> u ,\ v </tex> такие, что <tex> s \cdot x = u ,\ u \cdot y = v ,\ v \cdot z \in T </tex>. Тогда справедливо равенство <tex> C_L(y) = \bigcup\limits_{(u, v) :\ u \cdot y = v} \{ \langle x, z \rangle \mid s \cdot x = u ,\ v \cdot z \in T \} </tex>. Учитывая <tex> | \{ (u, v) \mid u,v \in Q ,\ u \cdot y = v \} | = |Q| </tex>, получаем <tex> | \{ C_L(y) \mid y \in \Sigma^* \} | \leqslant 2^{|Q|} </tex>, то есть множество контекстов конечно. | + | Пусть <tex>L</tex> {{---}} регулярный. Тогда существует детерминированный автомат <tex>\mathcal{A}</tex>, распознающий его. Понятно, что для любого слова <tex> xyz </tex>, допускаемого автоматом, существуют <tex> u ,\ v </tex> такие, что <tex> s \cdot x = u ,\ u \cdot y = v ,\ v \cdot z \in T </tex> (где <tex> s </tex> {{---}} начальное состояние). Тогда справедливо равенство <tex> C_L(y) = \bigcup\limits_{(u, v) :\ u \cdot y = v} \{ \langle x, z \rangle \mid s \cdot x = u ,\ v \cdot z \in T \} </tex>. Учитывая <tex> | \{ (u, v) \mid u,v \in Q ,\ u \cdot y = v \} | = |Q| </tex>, получаем <tex> | \{ C_L(y) \mid y \in \Sigma^* \} | \leqslant 2^{|Q|} </tex>, то есть множество контекстов конечно. |
}} | }} | ||
| Строка 150: | Строка 160: | ||
'''3'''. Язык <tex>L = 0^n1^n</tex> задан над алфавитом <tex>\Sigma = \{0,1\}</tex>. Балансом слова <tex>|\omega|_b</tex> назовём число, равное разности между количеством нулей и единиц, встречающихся в данном слове. Если слово <tex>\omega = uxv</tex> принадлежит языку <tex>L</tex>, то <tex>|x|_b = -(|u|_b + |v|_b)</tex>. Но <tex>|x|_b</tex> может принимать любое целое значение, при том, что <tex>x</tex> имеет непустой двухсторонний контекст. Значит, синтаксический моноид <tex>M(L)</tex> имеет бесконечное количество элементов, что значит, что данный язык не является регулярным. | '''3'''. Язык <tex>L = 0^n1^n</tex> задан над алфавитом <tex>\Sigma = \{0,1\}</tex>. Балансом слова <tex>|\omega|_b</tex> назовём число, равное разности между количеством нулей и единиц, встречающихся в данном слове. Если слово <tex>\omega = uxv</tex> принадлежит языку <tex>L</tex>, то <tex>|x|_b = -(|u|_b + |v|_b)</tex>. Но <tex>|x|_b</tex> может принимать любое целое значение, при том, что <tex>x</tex> имеет непустой двухсторонний контекст. Значит, синтаксический моноид <tex>M(L)</tex> имеет бесконечное количество элементов, что значит, что данный язык не является регулярным. | ||
| − | == | + | == Источники информации == |
* ''Howard Straubing'' Finite automata, formal logic, and circuit complexity, 1994. ISBN 3-7643-3719-2. {{---}} C. 53. | * ''Howard Straubing'' Finite automata, formal logic, and circuit complexity, 1994. ISBN 3-7643-3719-2. {{---}} C. 53. | ||
* ''James A. Anderson'' Automata theory with modern applications, 2006. ISBN 0-521-61324-8. {{---}} С. 72. | * ''James A. Anderson'' Automata theory with modern applications, 2006. ISBN 0-521-61324-8. {{---}} С. 72. | ||
| − | * [http://en.wikipedia.org/wiki/Syntactic_monoid Syntactic monoid - Wikipedia] | + | * [http://en.wikipedia.org/wiki/Syntactic_monoid Syntactic monoid {{---}} Wikipedia] |
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Автоматы и регулярные языки]] | [[Категория: Автоматы и регулярные языки]] | ||
Версия 22:58, 23 ноября 2014
Содержание
Контексты
Правый контекст
| Определение: |
| Правым контекстом (англ. right context) слова в языке называется множество . |
| Лемма: |
Язык — регулярный множество его правых контекстов конечно. |
| Доказательство: |
|
Покажем что полученный автомат допускает в точности указанный язык. По построению выполняется
Из 1 следует
Положив и учтя 2, получим В таких условиях (мы фиксируем за состоянием контекст ) левая часть 3 равносильна , а правая означает, что автомат допускает .
|
Примеры
Здесь будем понимать под не стандартное отображение множества в множество, а . Рассмотрим правые контексты следующих языков:
-
- Возникающие правые контексты:
- , где — множество остальных аргументов.
- Начальное состояние — 1 ( рассматривалось в нём).
- Допускающие состояния: 4, 7, 9 (в них ).
- Состояние 10 — дьявольское.
- Возникающие правые контексты:
-
- Возможные правые контексты (аргументы упорядочены в лексикографическом порядке):
- Итого 4 состояния; начальное состояние 1, допускающее 4, состояние 3&5 — дьявольское.
- Возможные правые контексты (аргументы упорядочены в лексикографическом порядке):
Левый контекст
| Определение: |
| Левым контекстом (англ. left context) слова в языке называется множество . |
| Лемма: |
Язык — регулярный множество его левых контекстов конечно. |
| Доказательство: |
| Поскольку множество регулярных языков замкнуто относительно операции разворота, то из того, что и аналогичного утверждения о правых контекстах получаем требуемое. |
Двухсторонний контекст
| Определение: |
| Двухсторонним контекстом (англ. two-sided context) слова в языке называется множество . |
Любопытное замечание: состоит из всех пар строк, которые при конкатенации дают слово из языка.
Для доказательства последующих утверждений будем использовать бинарное отображение со свойством .
| Лемма: |
Язык — регулярный множество его двухсторонних контекстов конечно. |
| Доказательство: |
|
|
Синтаксический моноид
Определения
| Определение: |
| Синтаксическим моноидом (англ. syntactic monoid) языка называется множество, состоящее из его классов эквивалентности , с введённым на нём операцией конкатенации , где . Нейтральным элементом в нём является . |
| Определение: |
| Групповой язык (англ. group language) — это язык, синтаксический моноид которого является группой. |
Свойства
Синтаксический моноид определён для любого , однако некоторые свойства языка можно определить по структуре его синтаксического моноида. Размер синтаксического моноида является мерой структурной сложности языка.
| Теорема: |
Язык — регулярный его синтаксический моноид конечен. |
| Доказательство: |
|
Размер синтаксического моноида языка равен количеству его различных двухсторонних контекстов . Применяя лемму, доказанную ранее, получаем: Язык — регулярный множество его двухсторонних контекстов конечно его синтаксический моноид конечен. |
| Лемма: |
Пусть язык распознается ДКА . Тогда размер его синтаксического моноида не превосходит . |
| Доказательство: |
|
Также введём на следующее отношение эквивалентности:
|
Пусть — ДКА. Каждое слово порождает отображение , определённое следующим образом: .
| Определение: |
| Моноидом переходов (англ. transition monoid) называется множество отображений с операцией композиции. . Нейтральным элементом в данном моноиде является отображение . |
| Теорема: |
Пусть — минимальный ДКА, задающий язык . Тогда и изоморфны. |
| Доказательство: |
|
Покажем, что .
|
Примеры
1. Рассмотрим язык .
— это множество всех пар , таких что . Значит, состоит из двух элементов: множества слов чётной длины и множества слов нечётной длины. Нейтральным элементом в данном моноиде является множество слов чётной длины. Оба элемента являются обратными самим себе, значит является группой, следовательно — групповой язык.
2. Язык над алфавитом задан регулярным выражением . Его синтаксический моноид содержит три элемента:
— нейтральный элемент. Включает в себя только пустую строку.
содержит все строки, распознаваемые регулярным выражением . .
содержит все строки, принадлежащие языку, то есть, распознаваемые регулярным выражением . .
Заметим, что и не имеют обратных элементов в данном моноиде, так как нейтральный элемент содержит только пустую строку, а её невозможно получить из непустой с помощью конкатенации. Следовательно не является групповым языком.
3. Язык задан над алфавитом . Балансом слова назовём число, равное разности между количеством нулей и единиц, встречающихся в данном слове. Если слово принадлежит языку , то . Но может принимать любое целое значение, при том, что имеет непустой двухсторонний контекст. Значит, синтаксический моноид имеет бесконечное количество элементов, что значит, что данный язык не является регулярным.
Источники информации
- Howard Straubing Finite automata, formal logic, and circuit complexity, 1994. ISBN 3-7643-3719-2. — C. 53.
- James A. Anderson Automata theory with modern applications, 2006. ISBN 0-521-61324-8. — С. 72.
- Syntactic monoid — Wikipedia