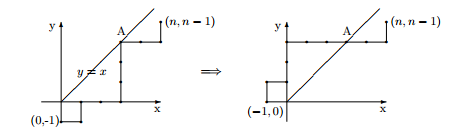Числа Каталана

Числа Каталана

Определение:

Числа Каталана — последовательность чисел, выражающих: количество не изоморфных упорядоченных бинарных деревьев с корнем и [math] n + 1 [/math] листьями количество способов соединения [math] 2n [/math] точек на окружности [math] n [/math] не пересекающимися хордами количество триангуляций выпуклого [math] n [/math]-угольника количество способов полностью разделить скобками [math] n + 1 [/math] множитель количество корректных скобочных последовательностей, состоящих из [math] n [/math] открывающих и [math] n [/math] закрывающих скобок

Первые несколько чисел Каталана:

[math] 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, ... [/math]

Формулы вычисления чисел Каталана

Рекуррентная формула

[math]C_n = \sum_{i = 0}^{n - 1} C_i C_{n - 1 - i} [/math]

Доказательство

Рекуррентную формулу легко вывести из задачи о правильных скобочных последовательностях.

Пусть [math]X[/math] - произвольная правильная скобочная последовательность длины [math]2n[/math]. Она начинается с открывающейся скобки. Найдем парную ей закрывающуюся скобку и представим последовательность [math]X[/math] в виде: [math]X = (A)B[/math], где [math]A[/math] и [math]B[/math] - тоже правильные скобочные последовательности. Если длина последовательности [math]A[/math] равна [math]2k[/math], то последовательность [math]A[/math] можно составить [math]C_k[/math] способами. Тогда длина последовательности [math]B[/math] равна [math]2(n - k - 1)[/math] и последовательность [math]B[/math] можно составить [math]C_{n - k - 1}[/math] способами. Комбинация любого способа составить последовательность [math]A[/math] с любым способом составить последовательность [math]B[/math] даст новую последовательность [math]X[/math], а величина [math]k[/math] может меняться от [math]0[/math] до [math]n - 1[/math]. Получили рекуррентное соотношение: [math]C_n = C_0 C_{n-1} + C_1 C_{n-2} + \cdot \cdot \cdot + C_{n-1} C_0 [/math]. Так как [math]C_0 = 1[/math], то последовательность совпадает с числами Каталана. Если занести всё под знак суммы, то получаем конечную формулу:

[math]C_n = \sum_{i = 0}^{n - 1} C_i C_{n - 1 - i} [/math]

Аналитическая формула

[math] C_n = \frac{1}{n+1} \binom {2n} {n} [/math]

Доказательство

Правильной скобочной структуре из [math]n[/math] открывающих и [math]n[/math] закрывающих скобок мы поставим в соответствие путь в квадрате [math][0, n]×[0, n][/math]. Путь начинается в точке [math](0,0)[/math] и заканчивается в точке [math](n, n)[/math]. Открывающей скобке мы сопоставляем горизонтальный отрезок длины [math]1[/math], а закрывающей — вертикальный. Если путь сопоставлен правильной структуре, то ни одна его точка не может лежать выше главной диагонали квадрата. Обратно, такому пути ("правильному пути") сопоставляется правильная скобочная структура. Геометрическое представление правильных скобочных структур позволяет найти выражение для чисел Каталана.

Сместим правильный путь на 1 клетку вниз. Теперь правильный путь начинается в точке [math] (0, -1) [/math], заканчивается в точке [math] (n, n-1) [/math] и не имеет общих точек с прямой [math] y = x [/math] — биссектрисой первого квадранта. Нам нужно найти количество правильных путей. Для этого мы найдем количество неправильных, и из общего числа путей вычтем количество неправильных. Мы рассматриваем пути из точки [math] (0, -1) [/math] в точку [math] (n, n-1) [/math]. Длина такого пути равна [math]2n[/math] и он содержит [math]n[/math] вертикальных сегментов и [math]n[/math] горизонтальных. Количество всех таких путей равно числу способов выбрать [math]n[/math] вертикальных сегментов из общего числа [math]2n[/math] сегментов, т.е. равно [math] \binom {2n}{n} [/math].

Рассмотрим неправильный путь и его первую точку на прямой [math] y = x [/math] (точка A). Отрезок пути от точки [math](0, -1)[/math] до точки A заменим симметричным относительно прямой [math]y = x[/math]. Мы получим путь длины [math]2n[/math], идущий из точки [math](-1, 0)[/math] в точку [math](n, n-1)[/math] (Смотри рис.).

Такой путь обязательно пересекает прямую [math] y = x [/math]. Обратно, пусть нам дан путь длины [math] 2n [/math] из точки [math](-1, 0)[/math] в точку [math](n, n-1)[/math] и пусть[math] A [/math] — первая точка этого пути, лежащая на прямой [math]y = x[/math]. Заменив участок пути от точки [math](-1, 0)[/math] до точки A на симметричный относительно прямой [math]y = x[/math], мы получим неправильный путь из точки [math](0, -1)[/math] в точку [math](n, n-1)[/math]. Следовательно, неправильных путей из точки [math](0, -1)[/math] в точку [math](n, n-1)[/math] столько же, сколько путей из точки [math](-1, 0)[/math] в точку [math](n, n-1)[/math]. Такой путь длины содержит [math]n+1[/math] горизонтальных и [math]n-1[/math] вертикальных участков. Поэтому, количество таких путей равно [math] \binom {2n}{n-1} [/math]. Значит, количество правильных путей (т.е. число Каталана [math]C_n[/math]) равно

[math] C_n = \binom {2n} {n} - \binom {2n} {n-1} = \frac{2n!}{n!n!} - \frac{2n!}{(n-1)!(n+1)!} = \frac{2n!}{n!} (\frac{1}{n!} - \frac{1}{(n-1)! (n+1)}) = \frac{2n!}{n!n!(n+1)} = \frac{1}{n+1} \binom {2n} {n} [/math]

Примеры

Задача разбиения выпуклого [math] n [/math]—угольника на треугольники не пересекающимися диагоналями

Разбиение выпуклого шестиугольника

Ответ на задачу при [math] n = 3 [/math] тривиален: никаких диагоналей проводить не надо. В четырёхугольнике можно провести любую из двух диагоналей, так что способов два. В пятиугольнике — из любой вершины две диагонали, [math] 5 [/math] способов. При [math] n = 6 [/math] — первый не вполне очевидный ответ: [math] 14 [/math] способов (см. рис.); чтобы не запутаться, сторона BC выделена и отдельно нарисованы разрезания, в которых к ней примыкают соответственно треугольники [math] BCA, BCF, BCE [/math] и [math] BCD [/math].

Для семиугольника можно выделить одну из сторон и расклассифицировать разрезания в зависимости от того, какой треугольник к этой стороне примыкает. Имеем 5 разных случаев. В первом и последнем из них количество разбиений равно 14, ибо после отрезания треугольника остаётся шестиугольник. Во втором и четвёртом случаях при вырезании треугольника семиугольник распадается на треугольник и пятиугольник. В третьем случае семиугольник распадается на два четырёхугольника. Поскольку каждый из них можно разбить двумя способами, получаем [math]2 \cdot 2 = 4[/math] варианта. Итак, семиугольник можно разбить всего [math] 14 + 5 + 2 \cdot 2 + 5 + 14 = 42 [/math] способами. Рассматривая восьмиугольник, аналогично получаем [math] 42 + 14 + 2 \cdot 5 + 5 \cdot 2 + 14 + 42 = 132 [/math] способа.Такие вычисления можно проводить и дальше.

Доказательство

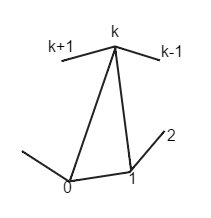
Пусть [math]t_n[/math] — число триангуляций [math] (n + 2) [/math] угольника при [math] n \geqslant 1 [/math]; положим [math] t_0 = 1 [/math]. Пронумеруем вершины многоугольника, начиная с произвольной против часовой стрелки. Рассмотрим произвольную триангуляцию и выделим треугольник, примыкающий к стороне 01 (см. рис.).

Пусть [math]k[/math] — номер третьей вершины этого треугольника. Выделенный треугольник разбивает [math](n + 2)[/math]-угольник на [math]k[/math]-угольник и [math](n-k+3)[/math]-угольник, каждый из которых триангулирован диагоналями. Перенумеруем вершины этих многоугольников против часовой стрелки так, чтобы нумерация вершин в каждом из них начиналась с 0. В результате получим пару триангуляций [math]k[/math]-угольника и [math](n-k+3)[/math]-угольника. Наоборот, каждая пара триангуляций [math]k[/math]-угольника и [math](n-k+3)[/math]-угольника определяет триангуляцию исходного многоугольника. Поэтому [math]t_{n+1} = t_0 t_n + t_1 t_{n-1} + \cdot \cdot \cdot + t_n t_0 [/math] и поскольку [math]t_0 = 1[/math], последовательность чисел [math]t_n[/math] совпадает с последовательностью Каталана.

Подсчет чисел Каталана

Будем вести подсчет с использованием метода динамического программирования. Пусть [math]d[i][j][/math] - число скобочных последовательностей длиной [math]i[/math] с балансом [math]j[/math]. Скобочную последовательность длиной [math]i[/math] с балансом [math]j[/math], можно получить из скобочной последовательности длины [math]i-1[/math] с балансом или [math]j-1[/math] (добавив в конец открывающуюся скобку), или [math]j+1[/math] (добавив в конец закрывающуюся скобку), т.е. [math]d[i][j] = d[i-1][j-1]+d[i-1][j+1][/math]. База [math]d[0][0][/math] = 1. Так же можно заметить, что максимальный баланс правильной скобочной последовательности длины [math]2n[/math], равен [math]n[/math]. [math] n [/math] -ое число Каталана будет храниться в ячейке [math]d[2n][0][/math].

Псевдокод:

function CatalanNumber(n: int)
 d[0][0] = 1
 for i = 1 to 2n
   for j = 0 to n
     d[i][j] = d[i-1][j-1] + d[i-1][j+1]
 return d[2n][0]

Таблица значений

Найдем значения таблицы для [math]n[/math] = 4

i\j	0	1	2	3	4	5	6	7	8
0	1	0	0	0	0	0	0	0	0
1	0	1	0	0	0	0	0	0	0
2	1	0	1	0	0	0	0	0	0
3	0	2	0	1	0	0	0	0	0
4	2	0	3	0	1	0	0	0	0
5	0	5	0	4	0	0	0	0	0
6	5	0	9	0	4	0	0	0	0
7	0	14	0	13	0	0	0	0	0
8	14	0	27	0	13	0	0	0	0

Смотри также

<wikitex>

• Двоичное дерево поиска
• Триангуляция полигонов

</wikitex>

Источники информации

<wikitex>

• MAXimal :: algo :: Числа Каталана
• Числа Каталана / Хабрахабр
• Числа Каталана — Википедия
• Журнал "Квант"
• Глава 5. Комбинаторика

</wikitex>