Коды Грея — различия между версиями
(→Алгоритм построения) |
Zernov (обсуждение | вклад) (Добавление <tex>) |
||
| Строка 12: | Строка 12: | ||
Существует несколько видов Кода Грея, самый простой из них {{---}} так называемый зеркальный двоичный Код Грея. Строится он так: | Существует несколько видов Кода Грея, самый простой из них {{---}} так называемый зеркальный двоичный Код Грея. Строится он так: | ||
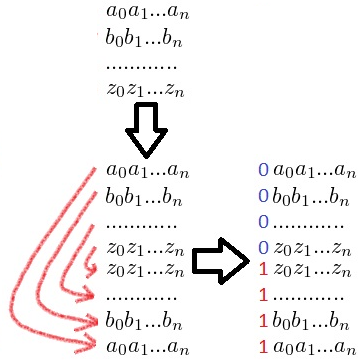
| − | Для получения кода длины <tex>n</tex> производится <tex>n</tex> шагов. На первом шаге код имеет длину 1 и состоит из двух векторов (0) и (1). На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается "0", а ко второй "1". С каждым шагом длина векторов увеличивается на 1, а их количество {{---}} вдвое. | + | Для получения кода длины <tex>n</tex> производится <tex>n</tex> шагов. На первом шаге код имеет длину <tex>1</tex> и состоит из двух векторов (<tex>0</tex>) и (<tex>1</tex>). На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается "<tex>0</tex>", а ко второй "<tex>1</tex>". С каждым шагом длина векторов увеличивается на <tex>1</tex>, а их количество {{---}} вдвое. |
Таким образом, количество векторов длины <tex>n</tex> равно <tex>2^n.</tex> | Таким образом, количество векторов длины <tex>n</tex> равно <tex>2^n.</tex> | ||
| Строка 41: | Строка 41: | ||
* на первом шаге код отвечает условиям | * на первом шаге код отвечает условиям | ||
* предположим, что код, получившийся на <tex>i</tex>-ом шаге, является Кодом Грея | * предположим, что код, получившийся на <tex>i</tex>-ом шаге, является Кодом Грея | ||
| − | * тогда на шаге <tex>i + 1</tex>: первая половина кода будет корректна, так как она совпадает с кодом с шага <tex>i</tex> за исключением добавленного последнего бита 0. Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит 1. На стыке: первые <tex>i</tex> бит совпадают в силу зеркальности, последние различны по построению. | + | * тогда на шаге <tex>i + 1</tex>: первая половина кода будет корректна, так как она совпадает с кодом с шага <tex>i</tex> за исключением добавленного последнего бита <tex>0</tex>. Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит <tex>1</tex>. На стыке: первые <tex>i</tex> бит совпадают в силу зеркальности, последние различны по построению. |
Таким образом, этот код {{---}} Код Грея. Индукционное предположение доказано, алгоритм работает верно. | Таким образом, этот код {{---}} Код Грея. Индукционное предположение доказано, алгоритм работает верно. | ||
| Строка 55: | Строка 55: | ||
В двоичном зеркальном коде Грея <tex>i</tex>-ый код может быть получен по формуле <tex>G_i = i \oplus (\lfloor i / 2 \rfloor)</tex> при нумерации кодов с нуля. | В двоичном зеркальном коде Грея <tex>i</tex>-ый код может быть получен по формуле <tex>G_i = i \oplus (\lfloor i / 2 \rfloor)</tex> при нумерации кодов с нуля. | ||
|proof = | |proof = | ||
| − | Для кода длиной 1 бит утверждение проверяется непосредственно. | + | Для кода длиной <tex>1</tex> бит утверждение проверяется непосредственно. |
Пусть существует зеркальный двоичный код Грея <tex>M</tex> длины <tex>n</tex>, для которого выполнено, что для любого <tex>i \enskip M_i = i \oplus (\lfloor i / 2 \rfloor)</tex> | Пусть существует зеркальный двоичный код Грея <tex>M</tex> длины <tex>n</tex>, для которого выполнено, что для любого <tex>i \enskip M_i = i \oplus (\lfloor i / 2 \rfloor)</tex> | ||
| Строка 78: | Строка 78: | ||
== Специальные типы кодов Грея == | == Специальные типы кодов Грея == | ||
=== Сбалансированный код Грея === | === Сбалансированный код Грея === | ||
| − | Несмотря на то, что зеркальный двоичный код Грея полезен во многих случаях, он не является оптимальным в некоторых ситуациях из-за отсутствия "однородности". В сбалансированном коде Грея, количество изменений в различных координатных позициях сделаны максимально приближенными настолько, насколько это возможно. Чтобы показать это точнее, пусть G - это R-ичный полный цикл Грея, имеющий последовательность перехода < | + | Несмотря на то, что зеркальный двоичный код Грея полезен во многих случаях, он не является оптимальным в некоторых ситуациях из-за отсутствия "однородности". В сбалансированном коде Грея, количество изменений в различных координатных позициях сделаны максимально приближенными настолько, насколько это возможно. Чтобы показать это точнее, пусть <tex>G</tex> - это <tex>R<//tex>-ичный полный цикл Грея, имеющий последовательность перехода <tex> (\delta_k)</tex>; отсчёты переходов(спектры) <tex>G</tex> являются наборами целых чисел, определенных как <math>\lambda_k = |\{ j \in \mathbb{Z}_{R^n} : \delta_j = k \}| \, , \text { for } k \in \mathbb{Z}_R</math>. |
| − | Код Грея является однородным или равномерно сбалансированным, если все его отсчёты переходов равны, и в этом случае у нас есть <math>\lambda_k = R^n / n</math> для всех <math>k</math>. Ясно, что при R = 2, такие коды существуют только при n = 2. В противном случае, если < | + | Код Грея является однородным или равномерно сбалансированным, если все его отсчёты переходов равны, и в этом случае у нас есть <math>\lambda_k = R^n / n</math> для всех <math>k</math>. Ясно, что при <tex>R = 2</tex>, такие коды существуют только при <tex>n = 2</tex>. В противном случае, если <tex>R^n</tex> не делится на <tex>n</tex> равномерно, то можно построить сбалансированные коды Грея, где каждый отсчёт перехода либо <math>\lfloor R^n / n \rfloor </math> либо <math> \lceil R^n / n \rceil</math>. Коды Грея также могут быть экспоненциально сбалансироваными, если все их отсчеты переходов являются смежными степеням двойки, и такие коды существуют для каждой степени двойки. |
=== Однодорожечный код Грея === | === Однодорожечный код Грея === | ||
| − | Еще один вид кода Грея - это однодорожечный код Грея. Разработан Спеддингом и уточнен Хильтгеном, Патерсоном и Брандестини. Однодорожечный код Грея является циклическим списком уникальных двоичных кодировок длины n так, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как < | + | Еще один вид кода Грея - это однодорожечный код Грея. Разработан Спеддингом и уточнен Хильтгеном, Патерсоном и Брандестини. Однодорожечный код Грея является циклическим списком уникальных двоичных кодировок длины <tex>n</tex> так, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как <tex>P_{xn}</tex> матрица, каждая колонка - это циклический сдвиг первого столбца. Название происходит от их использования датчиками вращения, где количество дорожек в настоящее время измеряется с помощью контактов, в результате для каждой дорожки на выход подаётся <tex>0</tex> или <tex>1</tex>. Чтобы снизить уровнень шума различных контактов не переключаясь в тот же момент времени, один датчик предпочтительно устанавливает дорожки так, что выход данных от контактов находится в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; для достижения точности хотя бы в <tex>1</tex> градус нужно, по крайней мере, <tex>360</tex> различных позиций на оборот, который требует минимум <tex>9</tex> бит данных, и тем самым такое же количество контактов. |
== Применение == | == Применение == | ||
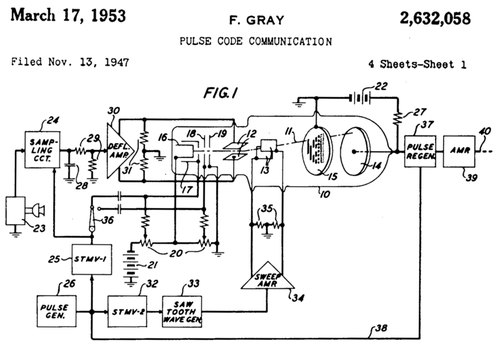
Фрэнк Грей изобрел метод для преобразования аналоговых сигналов в отраженные двоичные кодовые группы с использованием аппарата на основе вакуумной трубки. Способ и устройство были запатентованы в 1953 году, а код получил название код Грея. "PCM трубка" - аппарат, запатентованный Греем, был сделан Раймондом У. Сирсом из Bell Labs, работая с Греем и Уильямом М. Гудоллом. | Фрэнк Грей изобрел метод для преобразования аналоговых сигналов в отраженные двоичные кодовые группы с использованием аппарата на основе вакуумной трубки. Способ и устройство были запатентованы в 1953 году, а код получил название код Грея. "PCM трубка" - аппарат, запатентованный Греем, был сделан Раймондом У. Сирсом из Bell Labs, работая с Греем и Уильямом М. Гудоллом. | ||
[[Файл:PCM_Tube.png|500px|thumb|center|Часть первой страницы патента Грея, показывающая PCM трубку с отраженным двоичным кодом в тарелке.]] | [[Файл:PCM_Tube.png|500px|thumb|center|Часть первой страницы патента Грея, показывающая PCM трубку с отраженным двоичным кодом в тарелке.]] | ||
| − | * В технике коды Грея используются для минимизации ошибок при преобразовании аналоговых сигналов в цифровые (например, в [http://ru.wikipedia.org/wiki/%D0%AD%D0%BD%D0%BA%D0%BE%D0%B4%D0%B5%D1%80 датчиках-энкодерах]). В частности, коды Грея и были открыты в связи с этим применением. (Код Грея — это код преобразования бинарных символов в M-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. Обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в M-арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея. Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из < | + | * В технике коды Грея используются для минимизации ошибок при преобразовании аналоговых сигналов в цифровые (например, в [http://ru.wikipedia.org/wiki/%D0%AD%D0%BD%D0%BA%D0%BE%D0%B4%D0%B5%D1%80 датчиках-энкодерах]). В частности, коды Грея и были открыты в связи с этим применением. (Код Грея — это код преобразования бинарных символов в <tex>M</tex>-арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. Обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в <tex>M</tex>-арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея. Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из <tex>k = log_2 M</tex> переданных битов.) |
* Коды Грея используются для кодирования номера дорожек в жёстких дисках. | * Коды Грея используются для кодирования номера дорожек в жёстких дисках. | ||
* Код Грея можно использовать также и для решения задачи о [http://ru.wikipedia.org/wiki/%D0%A5%D0%B0%D0%BD%D0%BE%D0%B9%D1%81%D0%BA%D0%B8%D0%B5_%D0%B1%D0%B0%D1%88%D0%BD%D0%B8 Ханойских башнях]: | * Код Грея можно использовать также и для решения задачи о [http://ru.wikipedia.org/wiki/%D0%A5%D0%B0%D0%BD%D0%BE%D0%B9%D1%81%D0%BA%D0%B8%D0%B5_%D0%B1%D0%B0%D1%88%D0%BD%D0%B8 Ханойских башнях]: | ||
{{задача | {{задача | ||
|definition = | |definition = | ||
| − | Пусть n — количество дисков. Начнём с кода Грея длины n, состоящего из одних нулей (т.е. G(0)), и будем двигаться по кодам Грея (от G(i) переходить к G(i+1)). Поставим в соответствие каждому i-ому биту текущего кода Грея i-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита i как перемещение i-го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если n нечётно, то последовательность перемещений наименьшего диска имеет вид < | + | Пусть <tex>n</tex> — количество дисков. Начнём с кода Грея длины <tex>n</tex>, состоящего из одних нулей (т.е. <tex>G(0)</tex>), и будем двигаться по кодам Грея (от <tex>G(i)</tex> переходить к <tex>G(i+1)</tex>). Поставим в соответствие каждому <tex>i</tex>-ому биту текущего кода Грея <tex>i</tex>-ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита <tex>i</tex> как перемещение <tex>i</tex>-го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если <tex>n</tex> нечётно, то последовательность перемещений наименьшего диска имеет вид <tex>f \rightarrow t \rightarrow r \rightarrow f \rightarrow t \rightarrow r \rightarrow \ldots .</tex>(где <tex>f</tex> — стартовый стержень, <tex>t</tex> — финальный стержень, <tex>r</tex> — оставшийся стержень), а если <tex>n</tex> чётно, то <tex>f \rightarrow r \rightarrow t \rightarrow f \rightarrow r \rightarrow t \rightarrow \ldots.</tex> |
}} | }} | ||
* Коды Грея широко применяются в теории [http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BD%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC генетических алгоритмов] для кодирования генетических признаков, представленных целыми числами. | * Коды Грея широко применяются в теории [http://ru.wikipedia.org/wiki/%D0%93%D0%B5%D0%BD%D0%B5%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC генетических алгоритмов] для кодирования генетических признаков, представленных целыми числами. | ||
Версия 19:25, 20 декабря 2014
| Определение: |
| Код Грея (Gray code) — такое упорядочение -ичных (обычно двоичных) векторов, что соседние вектора отличаются только в одном разряде. |
Код назван в честь Фрэнка Грея, который в 1947-ом году получил патент на "отражённый двоичный код".
Содержание
Алгоритм построения
Существует несколько видов Кода Грея, самый простой из них — так называемый зеркальный двоичный Код Грея. Строится он так:
Для получения кода длины производится шагов. На первом шаге код имеет длину и состоит из двух векторов () и (). На каждом следующем шаге в конец списка заносятся все уже имеющиеся вектора в обратном порядке, и затем к первой половине получившихся векторов дописывается "", а ко второй "". С каждым шагом длина векторов увеличивается на , а их количество — вдвое. Таким образом, количество векторов длины равно
Псевдокод
|
GrayCode — двумерный массив, в котором GrayCode[a, b] — -ый бит в -ом коде Грея. buildCode(n):
GrayCode[1, n] = 0
GrayCode[2, n] = 1 {построение кода длины 1}
p = 2 {p — количество уже имеющихся кодов}
for (i = 2, i <= n, i++):
t = p
p = p * 2
for (k = p / 2 + 1, k <= p, k++):
GrayCode[k] = GrayCode[t] {отражение имеющихся кодов}
GrayCode[t, n + 1 - i] = 0
GrayCode[k, n + 1 - i] = 1 {добавление 0 и 1 в начало}
t--
|
Доказательство правильности работы алгоритма
По индукции:
- на первом шаге код отвечает условиям
- предположим, что код, получившийся на -ом шаге, является Кодом Грея
- тогда на шаге : первая половина кода будет корректна, так как она совпадает с кодом с шага за исключением добавленного последнего бита . Вторая половина тоже соответствует условиям, так как она является зеркальным отражением первой половины, только добавлен везде бит . На стыке: первые бит совпадают в силу зеркальности, последние различны по построению.
Таким образом, этот код — Код Грея. Индукционное предположение доказано, алгоритм работает верно.
Этот алгоритм можно обобщить и для -ичных векторов. Также известен алгоритм преобразования двоичного кода в Код Грея.
Существует ещё несколько видов Кода Грея — сбалансированный Код Грея, код Беккета-Грея, одноколейный Код Грея.
Явная формула для получения зеркального двоичного кода Грея
| Теорема: |
В двоичном зеркальном коде Грея -ый код может быть получен по формуле при нумерации кодов с нуля. |
| Доказательство: |
|
Для кода длиной бит утверждение проверяется непосредственно. Пусть существует зеркальный двоичный код Грея длины , для которого выполнено, что для любого Обозначим за код длины , полученный из описанным выше алгоритмом. Тогда: Для любого Для любого , где , то есть
Таким образом, шаг индукции доказан, следовательно, теорема верна. |
Специальные типы кодов Грея
Сбалансированный код Грея
Несмотря на то, что зеркальный двоичный код Грея полезен во многих случаях, он не является оптимальным в некоторых ситуациях из-за отсутствия "однородности". В сбалансированном коде Грея, количество изменений в различных координатных позициях сделаны максимально приближенными настолько, насколько это возможно. Чтобы показать это точнее, пусть - это ; отсчёты переходов(спектры) являются наборами целых чисел, определенных как . Код Грея является однородным или равномерно сбалансированным, если все его отсчёты переходов равны, и в этом случае у нас есть для всех . Ясно, что при , такие коды существуют только при . В противном случае, если не делится на равномерно, то можно построить сбалансированные коды Грея, где каждый отсчёт перехода либо либо . Коды Грея также могут быть экспоненциально сбалансироваными, если все их отсчеты переходов являются смежными степеням двойки, и такие коды существуют для каждой степени двойки.
Однодорожечный код Грея
Еще один вид кода Грея - это однодорожечный код Грея. Разработан Спеддингом и уточнен Хильтгеном, Патерсоном и Брандестини. Однодорожечный код Грея является циклическим списком уникальных двоичных кодировок длины так, что два последовательных слова отличаются ровно в одной позиции, и когда список рассматривается как матрица, каждая колонка - это циклический сдвиг первого столбца. Название происходит от их использования датчиками вращения, где количество дорожек в настоящее время измеряется с помощью контактов, в результате для каждой дорожки на выход подаётся или . Чтобы снизить уровнень шума различных контактов не переключаясь в тот же момент времени, один датчик предпочтительно устанавливает дорожки так, что выход данных от контактов находится в коде Грея. Чтобы получить высокую угловую точность, нужно много контактов; для достижения точности хотя бы в градус нужно, по крайней мере, различных позиций на оборот, который требует минимум бит данных, и тем самым такое же количество контактов.
Применение
Фрэнк Грей изобрел метод для преобразования аналоговых сигналов в отраженные двоичные кодовые группы с использованием аппарата на основе вакуумной трубки. Способ и устройство были запатентованы в 1953 году, а код получил название код Грея. "PCM трубка" - аппарат, запатентованный Греем, был сделан Раймондом У. Сирсом из Bell Labs, работая с Греем и Уильямом М. Гудоллом.
- В технике коды Грея используются для минимизации ошибок при преобразовании аналоговых сигналов в цифровые (например, в датчиках-энкодерах). В частности, коды Грея и были открыты в связи с этим применением. (Код Грея — это код преобразования бинарных символов в -арные, такие, что двоичные последовательности, соответствующие соседним символам (сдвигам фаз), отличаются только одним битом. Обычная бинарная кодировка сравнивается с кодировкой Грея. При появлении ошибки в -арном символе наиболее вероятными являются ближайшие соседние символы, отличающиеся от переданного лишь одним битом, если используется кодировка Грея. Таким образом, высока вероятность того, что при кодировании с помощью кода Грея в случае возникновения ошибки ошибочным будет только один из переданных битов.)
- Коды Грея используются для кодирования номера дорожек в жёстких дисках.
- Код Грея можно использовать также и для решения задачи о Ханойских башнях:
| Задача: |
| Пусть — количество дисков. Начнём с кода Грея длины , состоящего из одних нулей (т.е. ), и будем двигаться по кодам Грея (от переходить к ). Поставим в соответствие каждому -ому биту текущего кода Грея -ый диск (причём самому младшему биту соответствует наименьший по размеру диск, а самому старшему биту — наибольший). Поскольку на каждом шаге изменяется ровно один бит, то мы можем понимать изменение бита как перемещение -го диска. Заметим, что для всех дисков, кроме наименьшего, на каждом шаге имеется ровно один вариант хода (за исключением стартовой и финальной позиций). Для наименьшего диска всегда имеется два варианта хода, однако имеется стратегия выбора хода, всегда приводящая к ответу: если нечётно, то последовательность перемещений наименьшего диска имеет вид (где — стартовый стержень, — финальный стержень, — оставшийся стержень), а если чётно, то |
- Коды Грея широко применяются в теории генетических алгоритмов для кодирования генетических признаков, представленных целыми числами.
- Коды Грея используются в Картах Карно (при передаче в карту переменные сортируются в Код Грея).