Алгоритм Бржозовского — различия между версиями
(→Заключение) |
|||
| Строка 33: | Строка 33: | ||
== Заключение == | == Заключение == | ||
| − | Самым эффективным алгоритмом минимизации принято считать [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритм Хопкрофта]], который, как и прочие традиционные алгоритмы, работает только с [[Детерминированные_конечные_автоматы|ДКА]]. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритм Хопкрофта]]. В работе<ref>[http://citeseer.uark.edu:8080/citeseerx/viewdoc/summary;jsessionid=EF3DD7271F6E8907A154A540D93F2B0C?doi=10.1.1.59.8276]</ref>, сравнивающей оба алгоритма, показано, что алгоритм Бржозовского оказывается эффективнее [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритма Хопкрофта]] для автоматов с большим числом переходов. | + | Самым эффективным алгоритмом минимизации принято считать [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритм Хопкрофта]], который, как и прочие традиционные алгоритмы, работает только с [[Детерминированные_конечные_автоматы|ДКА]]. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритм Хопкрофта]]. В работе<ref>[http://citeseer.uark.edu:8080/citeseerx/viewdoc/summary;jsessionid=EF3DD7271F6E8907A154A540D93F2B0C?doi=10.1.1.59.8276 Deian Tabakov, Moshe Y. Vardi. Experimental evaluation of classical automata constructions]</ref>, сравнивающей оба алгоритма, показано, что алгоритм Бржозовского оказывается эффективнее [[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))|алгоритма Хопкрофта]] для автоматов с большим числом переходов. |
== См. также == | == См. также == | ||
| Строка 39: | Строка 39: | ||
*[[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))]] | *[[Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))]] | ||
| + | ==Примечания== | ||
| + | <references/> | ||
==Источники информации== | ==Источники информации== | ||
# [http://sovietov.com/txt/minfa/minfa.html Алгоритм Бржозовского для минимизации конечного автомата] | # [http://sovietov.com/txt/minfa/minfa.html Алгоритм Бржозовского для минимизации конечного автомата] | ||
| − | |||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Автоматы и регулярные языки]] | [[Категория: Автоматы и регулярные языки]] | ||
Версия 23:07, 30 декабря 2014
| Задача: |
| Пусть дан автомат . Требуется построить автомат с наименьшим количеством состояний, распознающий тот же язык, что и . |
Содержание
Алгоритм
Описание
Алгоритм минимизации конечных автоматов Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:
- Он элегантен и весьма оригинален.
- Он эффективен.
- Он работает даже с недетерминированными конечными автоматами.
Обладая обычными процедурами обращения и детерминизации конечного автомата, мы, с помощью идеи Бржозовского, можем немедленно приступить к минимизации заданного автомата. Для этого надо дважды провести его через обе вышеуказанные процедуры:
, где
- это исходный КА,
- это процедура обращения КА,
- это процедура детерминизации КА,
- это минимизированный КА.
Корректность
Пример работы
- Исходный НКА ():
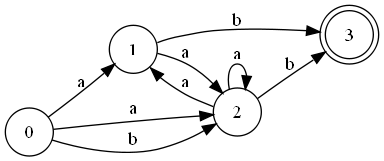
- Первый шаг алгоритма ():
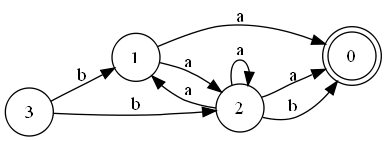
- Второй шаг алгоритма ():
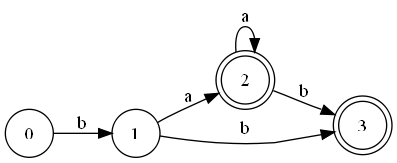
переименовывает состояния, после этого всегда является начальным состоянием - Третий шаг алгоритма ():
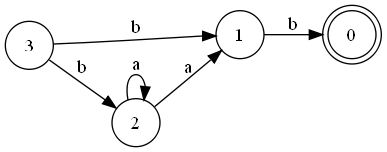
После выполнения этого шага алгоритма оба состояния и являются начальными. - Заключительный шаг алгоритма ():
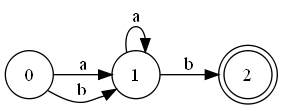
Заключение
Самым эффективным алгоритмом минимизации принято считать алгоритм Хопкрофта, который, как и прочие традиционные алгоритмы, работает только с ДКА. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и алгоритм Хопкрофта. В работе[1], сравнивающей оба алгоритма, показано, что алгоритм Бржозовского оказывается эффективнее алгоритма Хопкрофта для автоматов с большим числом переходов.
См. также
- Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний
- Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))