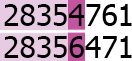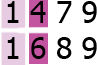Лексикографический порядок

Определение:

Пусть даны две последовательности [math] ~A = a_1 a_2 ... a_n [/math] и [math] ~B = b_1 b_2 ... b_m [/math] Тогда последовательность [math] ~A [/math] лексикографически меньше последовательности [math] ~B [/math], если выполняется одно из двух условий: [math] n \lt m [/math] и при этом [math] a_i = b_i [/math] для всех [math]i \in [1 .. n] [/math], [math] \mathcal {9} k\leqslant \min(n, m): a_k \lt b_k [/math] и при этом [math] \mathcal {8} j \lt k ~a_j = b_j [/math].

Приведем псевдокод сравнения последовательностей из элементов множества Т:

function Сompare(A, B : list <T>)   // Возвращает "LESS", если A < B, "MORE", если A > B, или "EQUAL", если последовательности равны
  for i = 1 to min(len(A), len(B)) 
    if A[i] < B[i]                  // i-й элемент А меньше i-го элемента B, но префиксы длины i - 1 равны
      return LESS
    if A[i] > B[i]                  // i-й элемент А больше i-го элемента B, но префиксы длины i - 1 равны
      return MORE
  if len(A) < len(B)                // А - префикс В, но не равна ей.
    return LESS
  if len(A) > len(B)                // В - префикс А, но не равна ей.
    return MORE
  return EQUAL                      // Длины последовательностей и все элементы равны

Определение:

Последовательности записаны в лексикографическом порядке (англ. lexicographical order), если для любых [math] i\lt j [/math] выполняется неравенство [math] S_i\lt S_j [/math], где [math] S_i [/math] и [math] S_j [/math] последовательности с номерами [math] i [/math] и [math] j [/math].

Например, слово "сон" лексикографически меньше слова "сонный", так как оно является его префиксом. Слово "низ" лексикографически меньше слова "нос", поскольку первые символы совпадают, а второй символ первого слова меньше, чем второй символ второго.

Примеры с комбинаторными объектами

Перестановки, общий префикс, 4 < 6, поэтому 1-ая перестановка лексикографически меньше

Сочетания, общий префикс, 4 < 6, поэтому 1-ое сочетание лексикографически меньше

Разбиение на слагаемые числа 14, общий префикс, 4 < 9, поэтому 1-ое разбиение лексикографически меньше

Другие примеры

• Последовательность чисел в любой системе счисления, записанных в фиксированной разрядной сетке (000, 001, 002, 003, 004, 005, [math]\dots[/math], 999).
• Порядок слов в словаре. Предполагается, что буквы можно сравнивать, сравнивая их номера в алфавите. Тогда лексикографический порядок — это, например, ААА, ААБ, ААВ, ААГ, [math]\dots[/math], ЯЯЯ.
• Эти слова тоже записаны в лексикографическом порядке: азбука, бог, борода, сон, сонный.

Ссылки

• Wikipedia — Lexicographical order
• Википедия — Лексикографический порядок