Дополняющая сеть, дополняющий путь

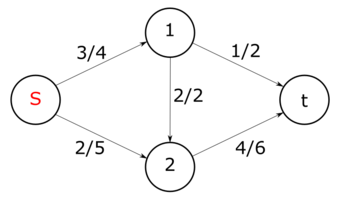
Определение:

Остаточной пропускной способностью (англ. Residual capacity) ребра [math](u, v)[/math] называется величина дополнительного потока, который мы можем направить из [math] u [/math] в [math] v [/math], не превысив пропускную способность [math] c(u, v) [/math]. Иными словами [math] c_f(u, v) = c(u, v) - f(u, v) [/math].

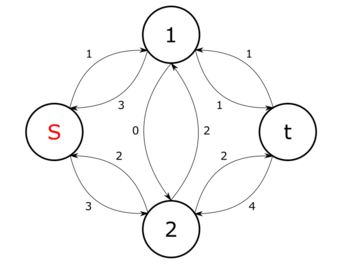
Определение:

Для заданной транспортной сети [math]G=(V,E)[/math] и потока [math]f[/math], остаточной сетью, (Дополняющая сеть, англ. Residual network) в [math]G[/math], порожденной потоком [math]f[/math], является сеть [math]G_f=(V,E_f)[/math], где [math]E_f=\{(u,v) \in V\times V : c_f(u, v) \gt 0\}[/math]

Определение:

Для заданных транспортной сети [math]G=(V,E)[/math] и потока [math]f[/math] дополняющим путем (англ. Augmenting path) [math]p[/math] является простой путь из истока в сток в остаточной сети [math]G_f=(V,E_f)[/math].

Граф с некоторым потоком

Остаточная сеть этого графа

Источники информации

• Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ.[1] — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296. ISBN — 978-0-2625-3196-2
• Википедия [math]-[/math] Транспортная сеть
• Wikipedia [math]-[/math] Flow Network(англ.)