Алгоритм Куна для поиска максимального паросочетания

Теорема

Теорема:

Если из вершины [math]x[/math] не существует дополняющей цепи относительно паросочетания [math]M[/math] и паросочетание [math]M'[/math] получается из [math]M[/math] изменением вдоль дополняющей цепи, тогда из [math]x[/math] не существует дополняющей цепи в [math]M'[/math].

Доказательство:

[math]\triangleright[/math]

Рисунок 1. Рисунок 2. Пунктиром обозначен путь между двумя вершинами. Ребро красного цвета лежит в паросочетании, а черного - нет. Доказательство от противного. Допустим в паросочетание внесли изменения вдоль дополняющей цепи [math](y \rightsquigarrow z)[/math] и из вершины [math]x[/math] появилась дополняющая цепь. Заметим, что эта дополняющая цепь должна вершинно пересекаться с той цепью, вдоль которой вносились изменения, иначе такая же дополняющая цепь из [math]x[/math] существовала и в исходном паросочетании. Пусть [math]p[/math] — ближайшая к [math]x[/math] вершина, которая принадлежит и новой дополняющей цепи и цепи [math](y \rightsquigarrow z)[/math]. Тогда [math]MP[/math] - последнее ребро на отрезке [math](y \rightsquigarrow p)[/math] цепи [math](y \rightsquigarrow z)[/math], [math]NP[/math] - последнее ребро на отрезке [math](z \rightsquigarrow p)[/math] цепи [math](y \rightsquigarrow z)[/math], [math]QP[/math] - последнее ребро лежащее на отрезке [math](x \rightsquigarrow p)[/math] новой дополняющей цепи(см. Рисунок 1). Допустим [math]MP[/math] принадлежит паросочетанию [math]M'[/math], тогда [math]NP[/math] ему не принадлежит. (Случай, когда [math]NP[/math] принадлежит паросочетанию [math]M'[/math] полностью симметричен.) Поскольку паросочетание [math]M'[/math] получается из [math]M[/math] изменением вдоль дополняющей цепи [math](y \rightsquigarrow z)[/math], в паросочетание [math]M[/math] входило ребро [math]NP[/math], а ребро [math]MP[/math] нет. Кроме того, ребро [math]QP[/math] не лежит ни в исходном паросочетании [math]M[/math], ни в паросочетании [math]M'[/math], в противном случае оказалось бы, что вершина [math]p[/math] инцидентна нескольким ребрам из паросочетания, что противоречит определению паросочетания. Тогда заметим, что цепь [math](x \rightsquigarrow z)[/math], полученная объединением цепей [math](x \rightsquigarrow p)[/math] и [math](p \rightsquigarrow z)[/math], по определению будет дополняющей в паросочетании [math]M[/math], что приводит к противоречию, поскольку в паросочетании [math]M[/math] из вершины [math]x[/math] не существует дополняющей цепи.

[math]\triangleleft[/math]

Алгоритм

Задан граф [math]G(V, E)[/math], про который известно, что он двудольный, но разбиение не задано явно.Требуется найти наибольшее паросочетание в нем

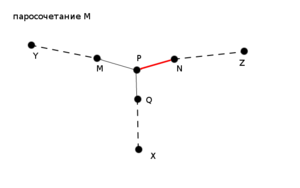
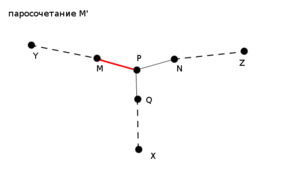
Алгоритм можно описать так: сначала возьмём пустое паросочетание, а потом — пока в графе удаётся найти увеличивающую цепь, — будем выполнять чередование паросочетания вдоль этой цепи, и повторять процесс поиска увеличивающей цепи. Как только такую цепь найти не удалось — процесс останавливаем, — текущее паросочетание и есть максимальное.

В массиве [math]matching[/math] хранятся паросочетания [math] (v, matching[v]) [/math] (Если паросочетания с вершиной [math] v [/math] не существует, то [math] matching[v] [/math] = -1). А [math]used[/math] - обычный массив "посещённостей" вершин в обходе в глубину (он нужен, чтобы обход в глубину не заходил в одну вершину дважды). Функция [math] \mathrm{dfs} [/math] возвращает [math]true[/math], если ей удалось найти увеличивающую цепь из вершины [math]v[/math], при этом считается, что эта функция уже произвела чередование паросочетания вдоль найденной цепи.

Внутри функции просматриваются все рёбра, исходящие из вершины [math]v[/math] первой доли, и затем проверяется: если это ребро ведёт в ненасыщенную вершину [math] to[/math], либо если эта вершина [math]to[/math] насыщена, но удаётся найти увеличивающую цепь рекурсивным запуском из [math]mt[to][/math], то мы говорим, что мы нашли увеличивающую цепь, и перед возвратом из функции с результатом [math]true[/math] производим чередование в текущем ребре: перенаправляем ребро, смежное с [math]to[/math], в вершину [math] v[/math].

В основной программе сначала указывается, что текущее паросочетание — пустое (список [math] mt[/math] заполняется числами -1). Затем перебирается вершина [math]v [/math] первой доли, и из неё запускается обход в глубину [math] \mathrm{dfs} [/math], предварительно обнулив массив [math] used[/math].

Стоит заметить, что размер паросочетания легко получить как число вызовов [math] \mathrm{dfs} [/math] в основной программе, вернувших результат [math] true [/math]. Само искомое максимальное паросочетание содержится в массиве [math] mt [/math]. После того, как все вершины [math]v \in V[/math] будут просмотрены, текущее паросочетание будет максимальным. Корректность алгоритма следует из теоремы о максимальном паросочетании и дополняющих цепях и теоремы, описанной выше.

Реализация

• Граф [math]G[/math] хранится списками смежности [math]g[v][i][/math]
• Функция [math]dfs(v)[/math] — обход в глубину, возвращает [math]true[/math], если есть увеличивающая цепь из вершины [math]v[/math].
• В массиве [math]matching[/math] хранятся паросочетания. Паросочетание есть ребро [math](i, matching[i])[/math].

bool dfs(v: int):
    if (used[v]):
        return false
    used[v] = true;
    for to in g[v]:
        if (matching[to] == -1 or dfs(matching[to])):
            matching[to] = v
            return true    
    return false

function main():
    fill(matching, -1)
    for v in V:
         fill(used, false)
         dfs(v)
    for v in V:
         if (matching[v] != -1):
              print(v, " ", matching[v])

Время работы

Итак, алгоритм Куна можно представить как серию из [math]n_1[/math] запусков обхода в глубину на всём графе.

Следовательно, всего этот алгоритм исполняется за время [math]O(nm)[/math], где [math]m[/math] — количество ребер, что в худшем случае есть [math]O(n^3)[/math].

Более точная оценка:

В описанной выше реализации запуски обхода в глубину/ширину происходят только из вершин первой доли, поэтому весь алгоритм исполняется за время [math]O(n_1m)[/math] , где [math]n_1[/math] — число вершин первой доли. В худшем случае это составляет [math]O(n_1^2n_2)[/math], где [math]n_2[/math] — число вершин второй доли.

Ссылки

• Теорема о максимальном паросочетании и дополняющих цепях
• Алгоритм Форда-Фалкерсона для поиска максимального паросочетания

Источники

• MAXimal :: algo :: Алгоритм Куна нахождения наибольшего паросочетания
  
• Асанов М., Баранский В., Расин В. — Дискретная математика: Графы, матроиды, алгоритмы — СПб.: Издательство "Лань", 2010. — 291 стр.