Алгоритмы на деревьях — различия между версиями
Kano vas (обсуждение | вклад) |
Kano vas (обсуждение | вклад) |
||
| Строка 95: | Строка 95: | ||
=== Алгоритм === | === Алгоритм === | ||
| + | ==== Наивный алгоритм ==== | ||
| + | Найдём центр графа исходя из его определения. | ||
* Построим матрицу <tex>A_{n \times n}</tex> (<tex>n</tex> — мощность множества <tex>V</tex>), где <tex>a_{ij} = d_{ij}</tex>, то есть матрицу кратчайших путей. Для её построения можно воспользоваться [[Алгоритм_Флойда|алгоритмом Флойда-Уоршелла]] или [[Алгоритм_Дейкстры|Дейкстры]]. | * Построим матрицу <tex>A_{n \times n}</tex> (<tex>n</tex> — мощность множества <tex>V</tex>), где <tex>a_{ij} = d_{ij}</tex>, то есть матрицу кратчайших путей. Для её построения можно воспользоваться [[Алгоритм_Флойда|алгоритмом Флойда-Уоршелла]] или [[Алгоритм_Дейкстры|Дейкстры]]. | ||
* Подсчитаем максимум в каждой строчке матрицы <tex>A</tex>. Таким образом, получим массив длины <tex>n</tex>. | * Подсчитаем максимум в каждой строчке матрицы <tex>A</tex>. Таким образом, получим массив длины <tex>n</tex>. | ||
* Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами. | * Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами. | ||
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет <tex>O(V^3)</tex>, а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и <tex>O(V^2)</tex>, за которую мы находим максимумы в матрице. | Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет <tex>O(V^3)</tex>, а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и <tex>O(V^2)</tex>, за которую мы находим максимумы в матрице. | ||
| + | |||
| + | ==== Алгоритм для дерева за O(n) ==== | ||
| + | Найдём центр дерева, действуя как в доказанной выше теореме. | ||
| + | |||
| + | Будем удалять висячие вершины (или "обрезать листья"), пока в дереве не останется одна или две вершины — они и будут центрами. | ||
== См. также == | == См. также == | ||
Версия 07:48, 12 января 2015
Содержание
Диаметр дерева
| Определение: |
| Диаметр дерева (diameter of a tree) — максимальная длина (в рёбрах) кратчайшего пути в дереве между любыми двумя вершинами. |
Пусть дан граф . Тогда диаметром называется , где — кратчайшее расстояние между вершинами.
Алгоритм
- Возьмём любую вершину и найдём расстояния до всех других вершин.
- Возьмём вершину такую, что для любого . Снова найдём расстояние от до всех остальных вершин. Самое большое расстояние — диаметр дерева.
Расстояние до остальных вершин будем искать алгоритмом .
Реализация
int diameterTree(graph<node> g) //тип node содержит поле number, в котором хранится номер вершины в графе
v = u = w = 0
d = bfs(g, v)
for i = 0, i < n, i++
if d[i] > d[u]
u = i
bfs(g, u)
for i = 0, i < n, i++
if d[i] > d[w]
w = i
return d[w]
Обоснование корректности
Будем пользоваться свойством, что в любом дереве больше одного листа. Исключительный случай — дерево из одной вершины, но алгоритм сработает верно и в этом случае.
| Теорема: |
Искомое расстояние — расстояние между двумя листами. |
| Доказательство: |
| Пусть искомое расстояние — расстояние между вершинами , где не является листом. Так как не является листом, то её степень больше единицы, следовательно, из неё существует ребро в непосещённую вершину (дважды посетить вершину мы не можем). |
После запуска алгоритма получим дерево .
| Теорема: |
В дереве не существует ребер между вершинами из разных поддеревьев некоторого их общего предка. |
| Доказательство: |
|
Предположим, существует ребро между соседними поддеревьями: Рассмотрим первую вершину, в которую приведет наш алгоритм, пусть это вершина , тогда в ходе рассмотрения всех смежных вершин мы добавим в список вершину , тем самым исключив возможность попадания их в разные поддеревья. |
Мы свели задачу к нахождению вершины , такой что сумма глубин поддеревьев максимальна.
Докажем, что одно из искомых поддеревьев содержит самый глубокий лист. Пусть нет, тогда, взяв расстояние от до глубочайшего листа, мы можем улучшить ответ.
Таким образом мы доказали, что нам нужно взять вершину с наибольшей глубиной после первого , очевидно, что ей в пару надо сопоставить вершину , такую что максимально. Вершину можно найти запуском из .
Оценка времени работы
Все операции кроме — . работает за линейное время, запускаем мы его два раза. Получаем .
Центр дерева
Определения
| Определение: |
| Эксцентриситет вершины (eccentricity of a vertex) — , где — множество вершин связного графа . |
| Определение: |
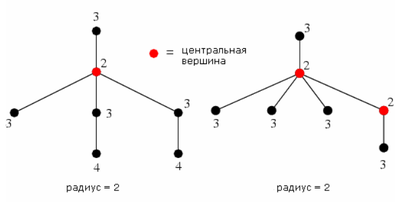
| Радиус (radius) — наименьший из эксцентриситетов вершин графа . |
| Определение: |
| Центральная вершина (central vertex) — вершина графа , такая что |
| Определение: |
| Центр графа (center of a graph) — множество всех центральных вершин графа . |
| Теорема: |
Каждое дерево имеет центр, состоящий из одной вершины или из двух смежных вершин. |
| Доказательство: |
| Утверждение очевидно для деревьев с одной и двумя вершинами. Покажем, что у любого другого дерева те же центральные вершины, что и у дерева , полученного из удалением всех его висячих вершин. Расстояние от данной вершины дерева до любой другой вершины достигает наибольшего значения, когда – висячая вершина. Таким образом, эксцентриситет каждой вершины дерева точно на единицу меньше эксцентриситета этой же вершины в дереве , следовательно, центры этих деревьев совпадают. Продолжим процесс удаления и получим требуемое. |
Алгоритм
Наивный алгоритм
Найдём центр графа исходя из его определения.
- Построим матрицу ( — мощность множества ), где , то есть матрицу кратчайших путей. Для её построения можно воспользоваться алгоритмом Флойда-Уоршелла или Дейкстры.
- Подсчитаем максимум в каждой строчке матрицы . Таким образом, получим массив длины .
- Найдём наименьший элемент в этом массиве. Эта вершина и есть центр графа. В том случае, когда вершин несколько, все они являются центрами.
Асимптотика зависит от используемого способа подсчета кратчайших путей. При Флойде это будет , а при Дейкстре — максимум из асимптотики конкретной реализации Дейкстры и , за которую мы находим максимумы в матрице.
Алгоритм для дерева за O(n)
Найдём центр дерева, действуя как в доказанной выше теореме.
Будем удалять висячие вершины (или "обрезать листья"), пока в дереве не останется одна или две вершины — они и будут центрами.
См. также
Источники информации
- Wikipedia — Distance (graph theory)
- Ф. Харари: Теория графов
- А. Клебанов: Центры графов