Участник:Kabanov — различия между версиями
Kabanov (обсуждение | вклад) |
Kabanov (обсуждение | вклад) (Локализация в ППЛГ) |
||
| Строка 1: | Строка 1: | ||
| − | == | + | ==Решение методом полос== |
| − | + | [[Файл:cgslabs.png|200px|right]] | |
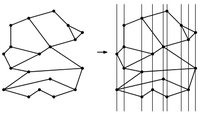
| − | + | Проведём через каждую вершину вертикальную прямую. Получим полосы (slabs). Пусть каждой полосе соответствует точка, через которую проведён левый край полосы. Будем хранить отсортированный массив <tex>x</tex>-координат, тогда за <tex>O(\log n)</tex> можно найти, в какой полосе лежит <tex>P</tex>. | |
| − | + | ||
| − | + | В каждой полосе отрезки, составляющие ППЛГ, могут пересекаться только в концах, причём эти точки пересечения могут лежать только на прямых, ограничивающих полосы (по построению). Получается, что внутри каждой полосы можно отсортировать отрезки, которые лежат в ней, например, снизу вверх. Тогда, найдя нужную полосу, можно быстро найти нужный отрезок. | |
| − | + | ||
| − | + | ===Персистентные деревья=== | |
| − | + | Персистентные структуры данных — это структуры, боже царя хранящие историю своих изменений. Персистентность бывает полная (когда можем изменять любую версию) и частичная (когда можем изменить только последнюю версию, но запросы можем делать на всех). | |
| − | + | ||
| − | + | Один из способов сделать дерево частично персистентным — node-copying (или path-copying, в разных источниках по-разному). Храним массив корней дерева. Когда нам нужно изменить ноду, мы создаём в этом массиве новый корень, но его поля left и right совпадают с таковыми в предыдущем корне. Далее мы идём от корня к ноде, которую хотим изменить. Все вершины по пути мы «копируем» так же, как и корень, при этом у предка меняем соответствующий указатель на новый. После этого мы меняем нужную нам ноду. Таким образом, для такого дерева нам нужно <tex>O(n \log n)</tex> памяти. | |
| − | + | ||
| − | + | Можно усовершенствовать этот способ. Теперь в каждой ноде будет храниться номер версии и поля для ленивого изменения дерева: фиксированное количество запасных указателей left и right и номера версий для них. Когда мы хотим изменить ноду, вместо копирования записываем изменения в запасные указатели, если они ещё есть, иначе создаём новую ноду и соответственно исправляем её предка. Для поиска по версиям используем бинпоиск. Этот способ называется limited node copying, для него нужно O(n) памяти, потому что амортизированно за один апдейт копируем O(1) нод. | |
| − | {{ | + | |
| − | + | ===Локализация в полосе=== | |
| − | | | + | Воспользуемся сбалансированным частично персистентным деревом для хранения отрезков в полосах. Каждая полоса — это новая версия дерева. |
| − | [[Файл: | + | |
| − | + | ==Время и память== | |
| + | На запрос нужно <tex>O(\log n)</tex>, на препроцессинг — <tex>O(n \log n)</tex>; памяти нужно <tex>O(n)</tex>. | ||
| + | |||
| + | ==Алгоритм Киркпатрика== | ||
| + | Существует ли метод локализации со временем поиска за <tex>O(\log n)</tex>, использующий менее чем квадратичную память? Эта задача оставалась не решенной довольно долго. Но все же была решена Липтоном и Тарьяном в 1977-1980 гг. Но их метод оказался на столько громоздким, а оценки времени его эффективности содержат слишком большую константу, что сами авторы не считали этот метод практичным, но его существование заставляет думать, что может найтись практичный алгоритм с временной оценкой <tex>O(\log n)</tex> и линейной памятью. | ||
| + | |||
| + | Недавно Киркпатриком был предложен оптимальный метод, дающий ответ на ожидания Липтона и Тарьяна, {{---}} детализация триангуляции. | ||
| + | ===Предобработка=== | ||
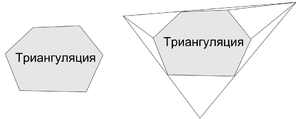
| + | <wikitex>[[Файл:кирк1.png|right|300px]]Пусть планарный N-вершинный граф задает триангуляцию нашего многоугольника (если это не так, то воспользуемся методом триангуляции многоугольника за время $O (n \log n)$. Напомним, что триангуляция на множестве вершин $V$ есть планарный граф с не более чем $3 |V| - 6$ ребрами ([[Формула_Эйлера |формула Эйлера]]). Для удобства описания алгоритма поместим нашу триангуляцию в охватывающий треугольник и построим триангуляцию области между нашими объектами. После этого преобразования все триангуляции будут обладать тремя границами и ровно $3 |V| - 6$ ребрами. | ||
| + | </wikitex> | ||
| + | |||
| + | ===Структура данных=== | ||
| + | <wikitex>[[Файл:кирк2.png|right|300px]] | ||
| + | [[Файл:кирк3.png|right|300px]] | ||
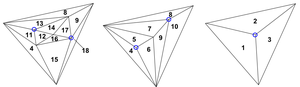
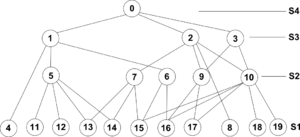
| + | Итак, имеется N-вершинная триангуляция $G$, и пусть строится последовательность триангуляций $S_1, S_2, \dots, S_{h(N)}$, где $S_1 = G$, а $S_i$ получается из $S_{i - 1}$ по следующим правилам: | ||
| + | * Шаг 1. Удалим некоторое количество неграничных и независимых (попарно несмежных друг с другом) вершин и инцидентные им ребра (от выбора этого множества напрямую зависит оптимальность алгоритма). | ||
| + | * Шаг 2. Построить триангуляцию получившихся в результате шага 1 многоугольников. | ||
| + | Таким образом $S_{h(N)}$ состоит из одного треугольника. Заметим, что все триангуляции имеют одну общую границу, так как удаляются только внутренние узлы. Далее, будем обозначать все треугольники как $R$, а также будем говорить, что треугольник $R_ij$ принадлежит триангуляции $S_i$, если | ||
| + | он был создан на шаге (2) при построении этой триангуляции. | ||
| + | |||
| + | Теперь построим структуру данных $T$ для поиска. Эта структура представляет собой направленный ацикличный граф, вершинами которого будут наши треугольники. Определим эту структуру следующим образом: из треугольника $R_k$ будет вести ребро в треугольник $R_j$, если при построении $S_i$ из $S_{i-1}$ мы имеем | ||
| + | * $R_j$ удалятся из $S_{i - 1}$ на шаге (1) | ||
| + | * $R_k$ создается в $S_{i}$ на шаге (2) | ||
| + | * $R_j \cap R_k \ne \varnothing $ | ||
| − | + | Очевидно, что треугольники из $S_1$ (и только они) не имеют исходящих ребер. | |
| − | |||
| − | |||
| − | + | Для ясности удобно изобразить $T$ в рассмотренном виде, то есть помещая его узлы в горизонтальные строки, каждая из | |
| − | + | которых соответствует какой-нибудь триангуляции. Последовательность триангуляций и соответствующая ей структура $T$ показаны на рисунке. Треугольники пронумерованы в порядке их появления. Кружком обведены вершины, которые удалены на данном шаге. </wikitex> | |
| − | + | ====Выбор множества удаляемых вершин==== | |
| − | + | <wikitex>Как уже упоминалось, от выбора множества вершит триангуляции, которые будут удалены при построении $S_i$ по $S_{i-1}$ существенно зависит эффективность метода. Предположим, что можно выбрать это множество так, чтобы выполнялись следующие ''свойства'' ($N_i$ обозначает число вершин в $S_i$): | |
| − | |||
| − | |||
| − | |||
| − | + | '''Свойство 1'''. $N_i = a_i N_{i-1}$, где $a_i \le a < 1$ для $i = 2,\dots , h(N)$. | |
| − | |||
| − | + | '''Свойство 2'''. Каждый треугольник $R_i \in S_i$ пересекается не более чем с $H$ треугольниками из $S_{i-1}$ и наоборот. | |
| − | + | Первое свойство немедленно влечет за собой следствие, что $h(N) \le \left \lceil \log_{1/a}N \right \rceil = O(log N)$, поскольку при переходе от $S_{i-1}$ к $S_i$ удаляется по меньшей мере фиксированная доля вершин. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Также из этих свойств следует, что память для $T$ равна $O(N)$. Действительно, заметим, что эта память используется для хранения узлов и указателей на их потомков. Из [[Формула_Эйлера|теоремы Эйлера]] о плоских графах следует, что $S_i$ содержит $F_i < 2N_i$ треугольников. Число узлов в $T$, представляющих треугольники из $S_i$, не превосходит $F_i$ (только те треугольники, которые действительно принадлежат $S_i$, появляются на соответствующем «ярусе» $T$). Отсюда следует, что общее число узлов в $T$ меньше, чем | |
| − | + | $2(N_1 + N_2 + \dots + N_{h(N)}) \le 2N_1(1 + a + a^2 + \dots + a^{h(N) - 1}) < \frac{2N}{1 - a}$. | |
| − | + | Что касается памяти, используемой под указатели, то по свойству 2 каждый узел имеет не более $H$ указателей, поэтому не более $\frac{2NH}{1-a}$ указателей появится в $T$. Это доказывает последнее утверждение. | |
| − | |||
| − | + | Покажем теперь, что критерий выбора множества удаляемых вершин, удовлетворяющий вышеописанным свойствам, существует. | |
| + | {{Теорема | ||
| + | |about= | ||
| + | критерий выбора множества удаляемых вершин | ||
| + | |statement= | ||
| + | Если на шаге (1) построения последовательности триангуляции удалять несмежные вершины со степенью меньше некоторого целого (будет указано позже) числа $K$, то свойства, описанные выше, будут выполнены. | ||
| + | |proof= | ||
| + | '''1. ''' Для проверки первого свойства воспользуемся некоторыми особенностями плоских графов. Из [[Формула_Эйлера | формулы Эйлера]] для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин $N$ и число ребер $e$ связаны соотношением | ||
| + | $e = 3N - 6$. | ||
| + | Пока в триангнуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин не меньше трех. Поскольку существует $3N - 6$ ребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше $6N$. Отсюда сразу следует, что не менее $ \frac{N}{2}$ вершин имеет степень меньше 12. Следовательно, пусть $K = 12$. Пусть также $v$ {{---}} число выбранных вершин. Поскольку каждой из них инцидентно не более $K-1 = 11$ ребер, а три граничные вершины не выбираются, то мы имеем | ||
| + | $v \ge \left \lfloor \frac{1}{12}(\frac{N}{2} - 3) \right \rfloor $. | ||
| + | Следовательно, $a \cong 1 - \frac{1}{24} < 0,959 < 1$, что доказывает справедливость свойства 1. | ||
| + | '''2. ''' Выполнение второго свойства обеспечивается тривиально. Поскольку удаление вершины со степенью меньше $K$ приводит к образованию многоугольника с числом ребер менее $K$, то каждый из удаленных треугольников пересекает не более $K - 2 = H$ новых треугольников. | ||
| + | }}</wikitex> | ||
| − | + | ===Поиск=== | |
| + | <wikitex>После построения структуры легко понять, как в ней происходит поиск. Элементарной операцией здесь является определение принадлежности треугольнику. Очевидно, что она выполняется константное время. Сначала мы локализуемся в треугольнике $S_1$. После этого мы строим путь от корневой вершины до листа следующим образом: находясь в какой-либо вершине $z$, просмотрим всех ее детей на принадлежность точки соответствующему треугольнику и, так как точка может находиться лишь в одном треугольнике конкретной триангуляции, перейдем в эту вершину, и продолжим поиск. | ||
| + | Этот поиск также можно рассматривать как последовательную локализацию в триангуляциях $S_1, \dots, S_{h(N)}$, откуда и происходит название самого метода. | ||
| + | </wikitex> | ||
| + | ====Псевдокод==== | ||
| + | <wikitex>Пусть все потомки узла $u$ из $T$ собраны в список successors(u), а triangle(u) обозначает треугольник, соответствующий узлу $u$. Тогда алгоритм поиска может выглядеть следующим образом: </wikitex> | ||
| + | procedure localization(z) | ||
| + | if (z not in triangle(root)) | ||
| + | z in infinite region | ||
| + | else | ||
| + | u = root | ||
| + | while (successors(u) != null) | ||
| + | for (v in successors(u)) | ||
| + | if (z in triangle(v)) | ||
| + | u = v | ||
| + | return u | ||
Версия 22:25, 20 января 2015
Содержание
Решение методом полос
Проведём через каждую вершину вертикальную прямую. Получим полосы (slabs). Пусть каждой полосе соответствует точка, через которую проведён левый край полосы. Будем хранить отсортированный массив -координат, тогда за можно найти, в какой полосе лежит .
В каждой полосе отрезки, составляющие ППЛГ, могут пересекаться только в концах, причём эти точки пересечения могут лежать только на прямых, ограничивающих полосы (по построению). Получается, что внутри каждой полосы можно отсортировать отрезки, которые лежат в ней, например, снизу вверх. Тогда, найдя нужную полосу, можно быстро найти нужный отрезок.
Персистентные деревья
Персистентные структуры данных — это структуры, боже царя хранящие историю своих изменений. Персистентность бывает полная (когда можем изменять любую версию) и частичная (когда можем изменить только последнюю версию, но запросы можем делать на всех).
Один из способов сделать дерево частично персистентным — node-copying (или path-copying, в разных источниках по-разному). Храним массив корней дерева. Когда нам нужно изменить ноду, мы создаём в этом массиве новый корень, но его поля left и right совпадают с таковыми в предыдущем корне. Далее мы идём от корня к ноде, которую хотим изменить. Все вершины по пути мы «копируем» так же, как и корень, при этом у предка меняем соответствующий указатель на новый. После этого мы меняем нужную нам ноду. Таким образом, для такого дерева нам нужно памяти.
Можно усовершенствовать этот способ. Теперь в каждой ноде будет храниться номер версии и поля для ленивого изменения дерева: фиксированное количество запасных указателей left и right и номера версий для них. Когда мы хотим изменить ноду, вместо копирования записываем изменения в запасные указатели, если они ещё есть, иначе создаём новую ноду и соответственно исправляем её предка. Для поиска по версиям используем бинпоиск. Этот способ называется limited node copying, для него нужно O(n) памяти, потому что амортизированно за один апдейт копируем O(1) нод.
Локализация в полосе
Воспользуемся сбалансированным частично персистентным деревом для хранения отрезков в полосах. Каждая полоса — это новая версия дерева.
Время и память
На запрос нужно , на препроцессинг — ; памяти нужно .
Алгоритм Киркпатрика
Существует ли метод локализации со временем поиска за , использующий менее чем квадратичную память? Эта задача оставалась не решенной довольно долго. Но все же была решена Липтоном и Тарьяном в 1977-1980 гг. Но их метод оказался на столько громоздким, а оценки времени его эффективности содержат слишком большую константу, что сами авторы не считали этот метод практичным, но его существование заставляет думать, что может найтись практичный алгоритм с временной оценкой и линейной памятью.
Недавно Киркпатриком был предложен оптимальный метод, дающий ответ на ожидания Липтона и Тарьяна, — детализация триангуляции.
Предобработка
<wikitex>Пусть планарный N-вершинный граф задает триангуляцию нашего многоугольника (если это не так, то воспользуемся методом триангуляции многоугольника за время $O (n \log n)$. Напомним, что триангуляция на множестве вершин $V$ есть планарный граф с не более чем $3 |V| - 6$ ребрами (формула Эйлера). Для удобства описания алгоритма поместим нашу триангуляцию в охватывающий треугольник и построим триангуляцию области между нашими объектами. После этого преобразования все триангуляции будут обладать тремя границами и ровно $3 |V| - 6$ ребрами.</wikitex>
Структура данных
<wikitex>Итак, имеется N-вершинная триангуляция $G$, и пусть строится последовательность триангуляций $S_1, S_2, \dots, S_{h(N)}$, где $S_1 = G$, а $S_i$ получается из $S_{i - 1}$ по следующим правилам:
- Шаг 1. Удалим некоторое количество неграничных и независимых (попарно несмежных друг с другом) вершин и инцидентные им ребра (от выбора этого множества напрямую зависит оптимальность алгоритма).
- Шаг 2. Построить триангуляцию получившихся в результате шага 1 многоугольников.
Таким образом $S_{h(N)}$ состоит из одного треугольника. Заметим, что все триангуляции имеют одну общую границу, так как удаляются только внутренние узлы. Далее, будем обозначать все треугольники как $R$, а также будем говорить, что треугольник $R_ij$ принадлежит триангуляции $S_i$, если он был создан на шаге (2) при построении этой триангуляции.
Теперь построим структуру данных $T$ для поиска. Эта структура представляет собой направленный ацикличный граф, вершинами которого будут наши треугольники. Определим эту структуру следующим образом: из треугольника $R_k$ будет вести ребро в треугольник $R_j$, если при построении $S_i$ из $S_{i-1}$ мы имеем
- $R_j$ удалятся из $S_{i - 1}$ на шаге (1)
- $R_k$ создается в $S_{i}$ на шаге (2)
- $R_j \cap R_k \ne \varnothing $
Очевидно, что треугольники из $S_1$ (и только они) не имеют исходящих ребер.
Для ясности удобно изобразить $T$ в рассмотренном виде, то есть помещая его узлы в горизонтальные строки, каждая из которых соответствует какой-нибудь триангуляции. Последовательность триангуляций и соответствующая ей структура $T$ показаны на рисунке. Треугольники пронумерованы в порядке их появления. Кружком обведены вершины, которые удалены на данном шаге. </wikitex>
Выбор множества удаляемых вершин
<wikitex>Как уже упоминалось, от выбора множества вершит триангуляции, которые будут удалены при построении $S_i$ по $S_{i-1}$ существенно зависит эффективность метода. Предположим, что можно выбрать это множество так, чтобы выполнялись следующие свойства ($N_i$ обозначает число вершин в $S_i$):
Свойство 1. $N_i = a_i N_{i-1}$, где $a_i \le a < 1$ для $i = 2,\dots , h(N)$.
Свойство 2. Каждый треугольник $R_i \in S_i$ пересекается не более чем с $H$ треугольниками из $S_{i-1}$ и наоборот. Первое свойство немедленно влечет за собой следствие, что $h(N) \le \left \lceil \log_{1/a}N \right \rceil = O(log N)$, поскольку при переходе от $S_{i-1}$ к $S_i$ удаляется по меньшей мере фиксированная доля вершин.
Также из этих свойств следует, что память для $T$ равна $O(N)$. Действительно, заметим, что эта память используется для хранения узлов и указателей на их потомков. Из теоремы Эйлера о плоских графах следует, что $S_i$ содержит $F_i < 2N_i$ треугольников. Число узлов в $T$, представляющих треугольники из $S_i$, не превосходит $F_i$ (только те треугольники, которые действительно принадлежат $S_i$, появляются на соответствующем «ярусе» $T$). Отсюда следует, что общее число узлов в $T$ меньше, чем $2(N_1 + N_2 + \dots + N_{h(N)}) \le 2N_1(1 + a + a^2 + \dots + a^{h(N) - 1}) < \frac{2N}{1 - a}$. Что касается памяти, используемой под указатели, то по свойству 2 каждый узел имеет не более $H$ указателей, поэтому не более $\frac{2NH}{1-a}$ указателей появится в $T$. Это доказывает последнее утверждение.
Покажем теперь, что критерий выбора множества удаляемых вершин, удовлетворяющий вышеописанным свойствам, существует.
| Теорема (критерий выбора множества удаляемых вершин): |
Если на шаге (1) построения последовательности триангуляции удалять несмежные вершины со степенью меньше некоторого целого (будет указано позже) числа $K$, то свойства, описанные выше, будут выполнены. |
| Доказательство: |
|
1. Для проверки первого свойства воспользуемся некоторыми особенностями плоских графов. Из формулы Эйлера для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин $N$ и число ребер $e$ связаны соотношением $e = 3N - 6$. Пока в триангнуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин не меньше трех. Поскольку существует $3N - 6$ ребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше $6N$. Отсюда сразу следует, что не менее $ \frac{N}{2}$ вершин имеет степень меньше 12. Следовательно, пусть $K = 12$. Пусть также $v$ — число выбранных вершин. Поскольку каждой из них инцидентно не более $K-1 = 11$ ребер, а три граничные вершины не выбираются, то мы имеем $v \ge \left \lfloor \frac{1}{12}(\frac{N}{2} - 3) \right \rfloor $. Следовательно, $a \cong 1 - \frac{1}{24} < 0,959 < 1$, что доказывает справедливость свойства 1. 2. Выполнение второго свойства обеспечивается тривиально. Поскольку удаление вершины со степенью меньше $K$ приводит к образованию многоугольника с числом ребер менее $K$, то каждый из удаленных треугольников пересекает не более $K - 2 = H$ новых треугольников. |
Поиск
<wikitex>После построения структуры легко понять, как в ней происходит поиск. Элементарной операцией здесь является определение принадлежности треугольнику. Очевидно, что она выполняется константное время. Сначала мы локализуемся в треугольнике $S_1$. После этого мы строим путь от корневой вершины до листа следующим образом: находясь в какой-либо вершине $z$, просмотрим всех ее детей на принадлежность точки соответствующему треугольнику и, так как точка может находиться лишь в одном треугольнике конкретной триангуляции, перейдем в эту вершину, и продолжим поиск. Этот поиск также можно рассматривать как последовательную локализацию в триангуляциях $S_1, \dots, S_{h(N)}$, откуда и происходит название самого метода. </wikitex>
Псевдокод
<wikitex>Пусть все потомки узла $u$ из $T$ собраны в список successors(u), а triangle(u) обозначает треугольник, соответствующий узлу $u$. Тогда алгоритм поиска может выглядеть следующим образом: </wikitex>
procedure localization(z)
if (z not in triangle(root))
z in infinite region
else
u = root
while (successors(u) != null)
for (v in successors(u))
if (z in triangle(v))
u = v
return u