Участник:Flanir1

2-3 дерево — структура данных, представляющая собой сбалансированное дерево поиска, такое что из каждого узла может выходить две или три ветви и глубина всех листьев одинакова. Является частным случаем B+-дерева, когда нелистовые вершины могут иметь только 2 или 3 сыновей.

Свойства

2-3 дерево — сбалансированное дерево поиска, обладающее следующими свойствами:

• нелистовые вершины имеют либо 2, либо 3 сына,
• нелистовая вершина, имеющая двух сыновей, хранит максимум левого поддерева. Нелистовая вершина, имеющая трех сыновей, хранит два значения.Первое значение хранит максимум левого поддерева, второе максимум центрального поддерева,
• сыновья упорядочены по значению максимума поддерева сына,
• все листья лежат на одной глубине,
• Высота 2-3 дерева [math]O(\log{n})[/math], где [math] n [/math] - количество элементов в дереве.

Теорема:

Высота 2-3 дерева [math]O(\log{n})[/math], где [math] n [/math] - количество элементов в дереве.

Доказательство:

[math]\triangleright[/math]

Из построения следует, что все листья лежат на одной глубине, так как элементов [math]n[/math], то получаем что высота равна [math]O(\log{n})[/math]

[math]\triangleleft[/math]

Операции

Введем следующие обозначения:

• [math]\mathtt{root}[/math] - корень 2-3 дерева

Каждый узел дерева обладает полями:

• [math]\mathtt{sons}[/math] - сыновья узла,
• [math]\mathtt{keys}[/math] - ключи узла,
• [math]\mathtt{length}[/math] - количество сыновей.

Поиск

• [math]x[/math] - искомое значение.
• [math]t[/math] - текущая вершина в дереве. Изначально [math]t = \mathtt{root}[/math]

Будем просматривать ключи в узлах, пока узел не является листом.Рассмотрим два случая: 1)у текущей вершины два сына. Если её значение меньше [math]x[/math], то [math]t = \mathtt{t.sons[1]}[/math], иначе [math]t = \mathtt{t.sons[0]}[/math].

2)у текущей вершины три сына. Если второе значение меньше [math]x[/math], то [math]t = \mathtt{t.sons[2]}[/math]. Если первое значение меньше [math]x[/math], то [math]t = \mathtt{t.sons[1]}[/math], иначе [math]t = \mathtt{t.sons[0]}[/math].

Node search(int x):
  Node t = root
  while (t не является листом)
    if (t.length == 2)
      if (t.keys[0] < x)
        t = t.sons[1]
      else t = t.sons[0]
    else
      if (t.keys[1] < x)
        t = t.sons[2]
      else
        if (t.keys[0] < x)
          t = t.sons[1]
        else t = t.sons[0]
  return t

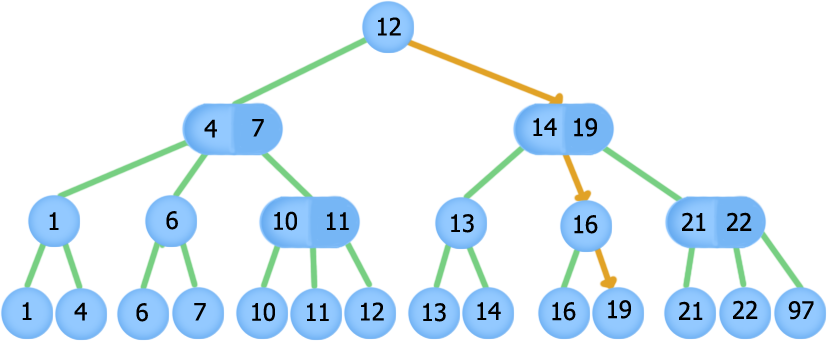
Пример поиска в 2-3 дереве, так как элемент 6 существует, то был возвращен корректный узел, так как элемента 10 нет, возвращается некорректный узел. На основе этого можно сделать метод [math]\mathtt{exist}[/math], проверяющий наличии элемента в дереве

Вставка элемента

• [math]x[/math] - добавляемое значение.
• [math]t[/math] - текущая вершина в дереве. Изначально [math]t = \mathtt{root}[/math]

Если корня не существует — дерево пустое, то новый элемент и будет корнем (одновременно и листом). Иначе поступим следующим образом:

Найдем сперва, где бы находился элемент, применив search(x). Далее проверим есть ли у этого узла родитель, если его нет, то в дереве всего один элемент - лист. Возьмем этот лист и новый узел, и создадим для них родителя, лист и новый узел расположим в порядке возрастания.

Если родитель существует, то подвесим к нему ещё одного сына. Если сыновей стало 4, то разделим родителя на два узла, и повторим разделение теперь для его родителя(перед разделением обновим ключи).

splitParent(Node t):
 if (t.length > 3) 
    Node a;
    a.sons[0] = t.sons[2]
    a.sons[1] = t.sons[3]
    t.sons[2].parent = a
    t.sons[3].parent = a
    a.keys[0] = t.keys[2]
    a.length = 2
    t.length = 2
    t.sons[2] = null
    t.sons[3] = null
    if (t.parent != null)
      t.parent[t.length] = a
      t.length++
      сортируем сыновей у t.parent
      splitParent(t.parent)
    else                   //мы расщепили корень, надо подвесить его к общему родителю, который будет новым корнем
     Node t = root
     root.sons[0] = t
     root.sons[1] = a
     t.parent = root
     a.parent = root
     root.length = 2
     сортируем сыновей у root

Если сыновей стало 3, то ничего не делаем. Далее необходимо восстановить ключи на пути от новой вершины до корня:

updateKeys(Node t): 
  Node a = t.parent
  while (a != null)
   for i = 0 .. a.length - 1
     a.keys[i] = max(a.sons[i]) //max - возвращает максимальное значение в поддереве.
   a = a.parent                 //Примечание: max легко находить, если хранить максимум 
                                //правого поддерева в каждом узле — это значение и будет max(a.sons[i])

[math]\mathtt{updateKeys}[/math] необходимо запускать от нового узла. Добавление элемента:

insert(int x):
Node n = Node(x)
if (root == null) 
 root = n
 return
Node a = search(x)
if (a.parent == null) 
  Node t = root
  root.sons[0] = t
  root.sons[1] = n
  t.parent = root
  n.parent = root
  root.length = 2
  сортируем сыновей у root
else 
  Node p = a.parent
  p.sons[p.length] = n
  p.length++
  n.parent = p
  сортируем сыновей у p
  updateKeys(n) 
  split(n)
updateKeys(n) 

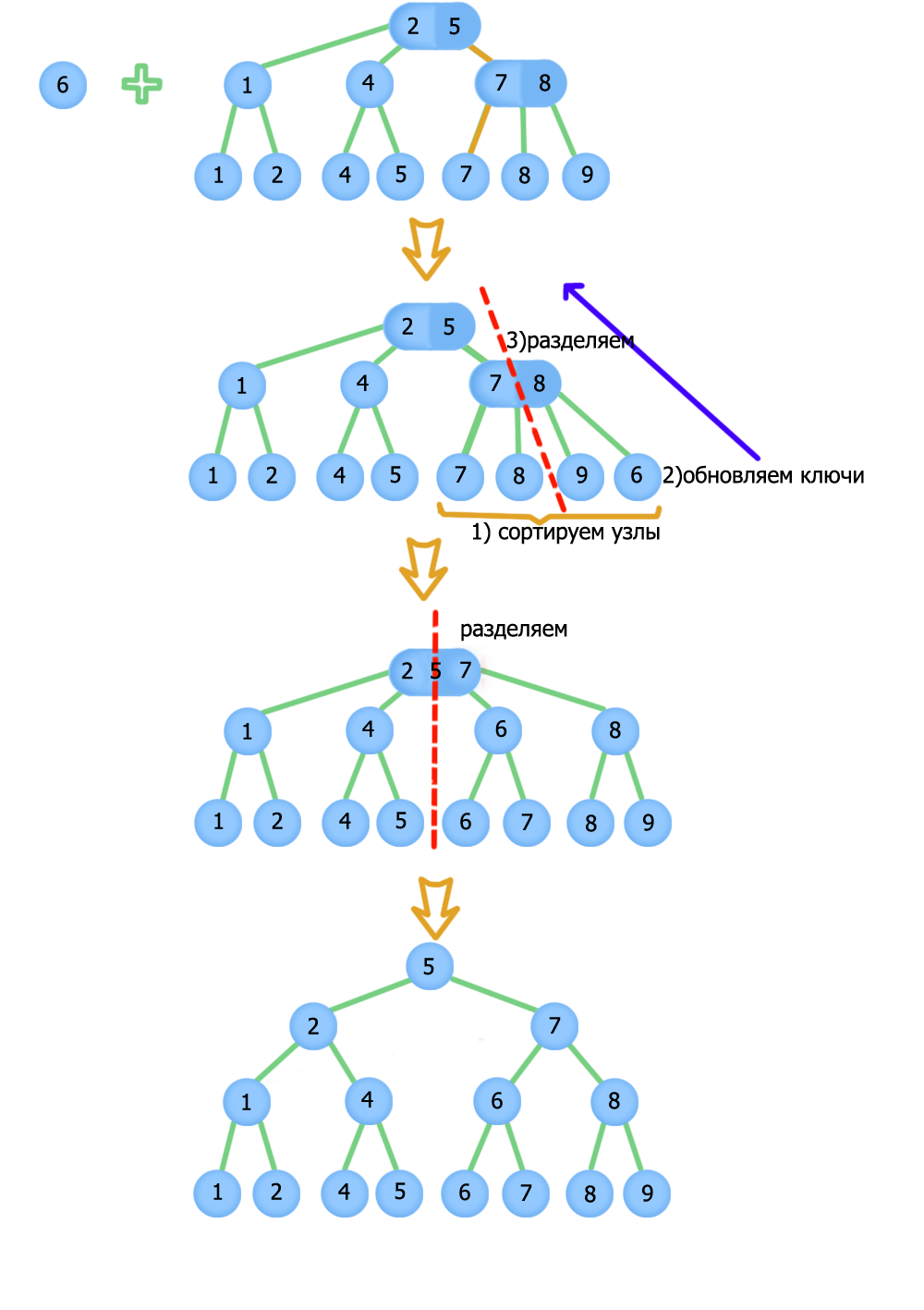
Так как мы спускаемся один раз, и поднимаемся вверх при расщеплении родителей не более одного раза, то [math]\mathtt{insert}[/math] работает за [math]O(\log{n})[/math]Примеры добавления:

Удаление элемента

[math]x[/math] — значение удаляемого узла. [math]t[/math] — текущий узел. Пусть изначально [math]t = \mathtt{search(x)}[/math]— узел, где находится x. Если у [math]t[/math] не существует родителя, то это корень. Удалим его. Если у [math]t[/math] существует родитель, и у него 3 сына, то просто удалим t.

Если у родителя([math]\mathtt{t.parent}[/math]) 2 сына, то удалим [math]t[/math], а его брата([math]b[/math] перецепим к родителю соседнего листа(обозначим его за [math]p[/math]). Вызовем [math]updateKey(b)[/math] и [math]splitParent(p)[/math], так как у [math]p[/math] могло оказаться 4 сына. Удалим теперь и [math]\mathtt{t.parent}[/math]. После возврата из рекурсии обновим все ключи с помощью [math]\mathtt{updateKeys()}[/math]. Будем запускаться от [math]b[/math]

Cсылки

• is.ifmo.ru - Визуализатор 2-3 дерева — 1
• rain.ifmo.ru - Визуализатор 2-3 дерева — 2
• Википедия — 2-3 дерево
• Д. Кнут «Искусство программирования. Сортировка и поиск», часть 6.2.4

См. также

• B-дерево
• Splay-дерево
• АВЛ-дерево
• Декартово дерево
• Красно-черное дерево