Диаграмма Вороного — различия между версиями
(→Диаграмма k-го порядка) |
|||
| Строка 38: | Строка 38: | ||
{{Теорема | {{Теорема | ||
|statement=Пусть <tex>P</tex> — множество из <tex>n</tex> сайтов. Если они все лежат на одной прямой, то <tex>Vor(P)</tex> представляет собой <tex>n - 1</tex> параллельную прямую. Иначе <tex>Vor(P)</tex> связная и все её рёбра — либо отрезки, либо лучи. | |statement=Пусть <tex>P</tex> — множество из <tex>n</tex> сайтов. Если они все лежат на одной прямой, то <tex>Vor(P)</tex> представляет собой <tex>n - 1</tex> параллельную прямую. Иначе <tex>Vor(P)</tex> связная и все её рёбра — либо отрезки, либо лучи. | ||
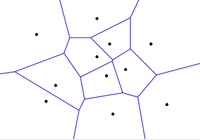
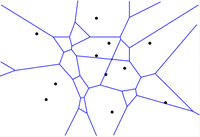
| − | |proof=[[Файл:voronoi-not-lines.png|200px | + | |proof=[[Файл:voronoi-not-lines.png|200px|right]] В случае, если все сайты лежат на одной прямой, каждая пара соседних сайтов порождает серединный перпендикуляр к отрезку, содержащему их, и, соответственно, к прямой, которая содержит все сайты. Так получаются <tex>n - 1</tex> прямая, каждая из которых перпендикулярна прямой, содержащей сайты, а значит, эти прямые параллельны. |
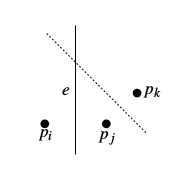
Рассмотрим теперь случай, когда сайты не лежат на одной прямой. Покажем, что рёбра — это отрезки или лучи, от противного. Предположим, что есть ребро <tex>e</tex>, являющееся прямой. Пусть оно — граница ячеек <tex>\mathcal{V}(p_i)</tex> и <tex>\mathcal{V}(p_j)</tex>. Пусть точка <tex>p_k \in P</tex> не лежит на прямой <tex>p_i p_j</tex> (по условию такая точка существует). Тогда серединный перпендикуляр к <tex>p_j p_k</tex> не параллелен <tex>e</tex>, и, значит, он его пересекает. Но тогда та часть <tex>e</tex>, что лежит в <tex>h(p_k, p_j)</tex>, не может быть границей <tex>\mathcal{V}(p_j)</tex>, потому что она ближе к <tex>p_k</tex>, чем к <tex>p_j</tex>. Пришли к противоречию. | Рассмотрим теперь случай, когда сайты не лежат на одной прямой. Покажем, что рёбра — это отрезки или лучи, от противного. Предположим, что есть ребро <tex>e</tex>, являющееся прямой. Пусть оно — граница ячеек <tex>\mathcal{V}(p_i)</tex> и <tex>\mathcal{V}(p_j)</tex>. Пусть точка <tex>p_k \in P</tex> не лежит на прямой <tex>p_i p_j</tex> (по условию такая точка существует). Тогда серединный перпендикуляр к <tex>p_j p_k</tex> не параллелен <tex>e</tex>, и, значит, он его пересекает. Но тогда та часть <tex>e</tex>, что лежит в <tex>h(p_k, p_j)</tex>, не может быть границей <tex>\mathcal{V}(p_j)</tex>, потому что она ближе к <tex>p_k</tex>, чем к <tex>p_j</tex>. Пришли к противоречию. | ||
| Строка 50: | Строка 50: | ||
{{Теорема | {{Теорема | ||
|statement=Для <tex>n \geqslant 3</tex> сайтов диаграмма Вороного содержит не больше <tex>2n - 5</tex> вершин и <tex> 3n - 6</tex> рёбер. | |statement=Для <tex>n \geqslant 3</tex> сайтов диаграмма Вороного содержит не больше <tex>2n - 5</tex> вершин и <tex> 3n - 6</tex> рёбер. | ||
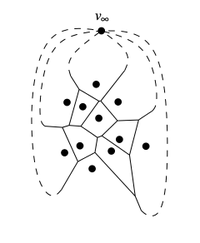
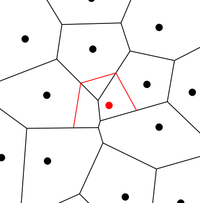
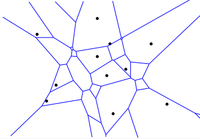
| − | |proof=[[Файл:voronoi-infinite-vertex.png|200px | + | |proof=[[Файл:voronoi-infinite-vertex.png|200px|right]]Для случая сайтов, лежащих на одной прямой, утверждение напрямую следует из вида диаграммы для этого случая, поэтому рассмотрим общий случай. По [[Формула Эйлера|формуле Эйлера]] <tex>v - e + f = 2</tex>, где <tex>v</tex> — число вершин, <tex>e</tex> — число рёбер и <tex>f</tex> — число граней связного планарного графа. Мы не можем сразу применить эту формулу к <tex>Vor(P)</tex>, потому что в этом графе есть полубесконечные рёбра. Поэтому добавим вершину <tex>n_\infty</tex>, и все полубесконечные рёбра мы превратим в рёбра, инцидентные ей. Таким образом мы увеличили число вершин на одну, а число рёбер не изменилось. Число граней равно <tex>n</tex> по определению диаграммы Вороного. Тогда по формуле Эйлера получаем <tex>(v + 1) - e + n = 2</tex>. |
Сумма степеней всех вершин полученного графа равна <tex>2e</tex>, так как у каждого ребра есть ровно два конца (нет петель). Также у из каждой вершины исходят как минимум три ребра. Отсюда получаем <tex>2e \geqslant 3 (n + 1)</tex>. | Сумма степеней всех вершин полученного графа равна <tex>2e</tex>, так как у каждого ребра есть ровно два конца (нет петель). Также у из каждой вершины исходят как минимум три ребра. Отсюда получаем <tex>2e \geqslant 3 (n + 1)</tex>. | ||
Домножим равенство на два и вычтем из него полученную нижнюю границу для <tex>2 \cdot e</tex>, в результате получим <tex> v \leqslant 2n - 5</tex>. Далее подставим этот результат в равенство и получим <tex>e \leqslant 3n - 6</tex>, что и требовалось доказать. | Домножим равенство на два и вычтем из него полученную нижнюю границу для <tex>2 \cdot e</tex>, в результате получим <tex> v \leqslant 2n - 5</tex>. Далее подставим этот результат в равенство и получим <tex>e \leqslant 3n - 6</tex>, что и требовалось доказать. | ||
| Строка 68: | Строка 68: | ||
{{Лемма | {{Лемма | ||
|statement=Серединный перпендикуляр к отрезку <tex>p_i p_j</tex> образует ребро диаграммы Вороного в том и только в том случае, если на нём есть точка <tex>q</tex> такая, что <tex>C_P(q)</tex> содержит на своей границе только сайты <tex>p_i, \ p_j</tex>. | |statement=Серединный перпендикуляр к отрезку <tex>p_i p_j</tex> образует ребро диаграммы Вороного в том и только в том случае, если на нём есть точка <tex>q</tex> такая, что <tex>C_P(q)</tex> содержит на своей границе только сайты <tex>p_i, \ p_j</tex>. | ||
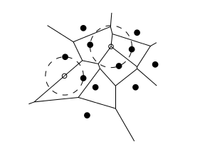
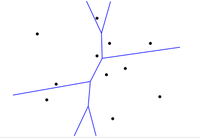
| − | |proof=[[Файл:voronoi-circles.png|200px | + | |proof=[[Файл:voronoi-circles.png|200px|right]]Предположим, что <tex>q</tex> существует. Тогда, так как <tex>C_P(q)</tex> не содержит в себе сайтов и содержит <tex>p_i, \ p_j</tex> на границе, <tex> \rho(q, p_i) = \rho(q, p_j) \leqslant \rho(q, p_k), \ 1 \leqslant k \leqslant n</tex>. Отсюда выходит, что <tex>q</tex> лежит — вершина <tex>Vor(P)</tex> или лежит на ребре диаграммы. Но по предыдущей лемме выходит, что <tex>q</tex> не может быть вершиной диаграммы. Значит, она лежит на ребре, заданном серединным перпендикуляром к <tex>p_i p_j</tex>. |
Докажем в другую сторону: пусть серединный перпендикуляр к <tex>p_i p_j</tex> задаёт ребро диаграммы. Наибольшая пустая окружность любой точки <tex>q</tex> на этом ребре должна содержать на границе <tex>p_i</tex> и <tex>p_j</tex>, и никаких других сайтов внутри. | Докажем в другую сторону: пусть серединный перпендикуляр к <tex>p_i p_j</tex> задаёт ребро диаграммы. Наибольшая пустая окружность любой точки <tex>q</tex> на этом ребре должна содержать на границе <tex>p_i</tex> и <tex>p_j</tex>, и никаких других сайтов внутри. | ||
}} | }} | ||
| Строка 97: | Строка 97: | ||
{| | {| | ||
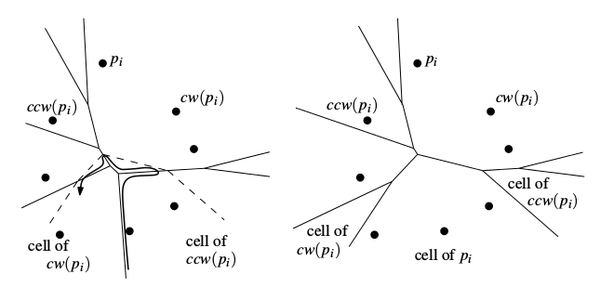
| − | |[[Файл:voronoi-incremental.png|200px|thumb]] | + | |[[Файл:voronoi-incremental.png|200px|thumb|Процесс построения диаграммы при добавлении новой точки]] |
| − | |[[Файл:voronoi-update-dcel.png|400px|thumb]] | + | |[[Файл:voronoi-update-dcel.png|400px|thumb|Обновление структуры при добавлении ребра]] |
|} | |} | ||
| Строка 125: | Строка 125: | ||
{| | {| | ||
| − | |[[Файл:voronoi-farthest-construct.png|600px|thumb]] | + | |[[Файл:voronoi-farthest-construct.png|600px|thumb|Построение очередной ячейки farthest-point диаграммы]] |
|} | |} | ||
Версия 22:31, 13 мая 2015
Содержание
Определения
Совсем неформальное определение
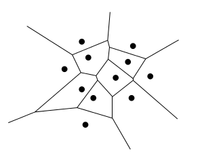
Пусть есть карта города, на которой точками обозначены почтовые отделения. Человек хочет отправить письмо, и он пойдёт на ближайшую почту. Ему интересно знать, какое отделение ближе, для любой точки города — необходимость отправить письмо может наступить неожиданно. Для этого он может взять карту и расчертить её на ячейки так, чтобы внутри каждой ячейки находилось только одно отделение, а для всех остальных точек ячейки именно эта почта была ближайшей. Полученная картинка и будет диаграммой Вороного для точек-почт.
Неформальное определение
Есть множество точек на плоскости. Кусочек плоскости из точек такой, что для всех ближайшей точкой из множества является одна и та же точка , называется ячейкой точки . Разбиение плоскости на такие ячейки для всех точек называется диаграммой Вороного для множества .
Формальное определение
— множество точек на плоскости.
| Определение: |
| называется сайтом (site). |
| Определение: |
| Ячейка Вороного (Voronoi cell, ) — множество точек плоскости таких, что для фиксированного сайта и любых других сайтов верно неравенство . |
| Определение: |
| Диаграмма Вороного (Voronoi diagram, ) для сайтов на плоскости — это разбиение плоскости на ячейки Вороного для каждого сайта из . |
В зависимости от контекста будем называть диаграммой Вороного как разбиение на ячейки, так и граф из вершин и рёбер, составляющих эти ячейки.
Свойства
Связь с пересечением полуплоскостей
Возьмём две точки плоскости: и . Проведём серединный перпендикуляр к отрезку ; полученную полуплоскость, которая содержит в себе , обозначим , другую — . Заметим, что для точки выполняется тогда и только тогда, когда . Отсюда вытекает следующее:
| Утверждение: |
Отсюда получаем, что что ячейка Вороного — это пересечение полуплоскостей, и поэтому представляет собой (возможно, неограниченную) открытую выпуклую область с не более чем вершинами и рёбрами.
Топология диаграммы Вороного
Размер структуры
| Теорема: |
Для сайтов диаграмма Вороного содержит не больше вершин и рёбер. |
| Доказательство: |
|
Для случая сайтов, лежащих на одной прямой, утверждение напрямую следует из вида диаграммы для этого случая, поэтому рассмотрим общий случай. По формуле Эйлера , где — число вершин, — число рёбер и — число граней связного планарного графа. Мы не можем сразу применить эту формулу к , потому что в этом графе есть полубесконечные рёбра. Поэтому добавим вершину , и все полубесконечные рёбра мы превратим в рёбра, инцидентные ей. Таким образом мы увеличили число вершин на одну, а число рёбер не изменилось. Число граней равно по определению диаграммы Вороного. Тогда по формуле Эйлера получаем .
Сумма степеней всех вершин полученного графа равна , так как у каждого ребра есть ровно два конца (нет петель). Также у из каждой вершины исходят как минимум три ребра. Отсюда получаем . Домножим равенство на два и вычтем из него полученную нижнюю границу для , в результате получим . Далее подставим этот результат в равенство и получим , что и требовалось доказать. |
Связь с триангуляцией Делоне
| Определение: |
| Наибольшая пустая окружность точки по отношению к (largest empty circle of with respect to , ) — наибольшая окружность с центром в такая, что во внутренности соответствующего ей круга не лежит ни одного сайта из . |
| Лемма: |
Точка — вершина диаграммы Вороного в том и только в том случае, когда содержит три и более сайтов на своей границе. |
| Доказательство: |
|
Предположим, что существует, а — соответствующие точки. Так как внутри нет других сайтов, должна быть на границе одновременно, то есть вершиной диаграмму. Докажем в другую сторону: каждая вершина диаграммы инцидентна минимум трём рёбрам, и, поэтому, как минимум трём ячейкам . Тогда лежит на равном расстоянии от и не может быть другого сайта ближе к , так как иначе не сойдутся в . Поэтому можно построить окружность с центром в и на границе так, что внутри не будет других сайтов. |
| Лемма: |
Серединный перпендикуляр к отрезку образует ребро диаграммы Вороного в том и только в том случае, если на нём есть точка такая, что содержит на своей границе только сайты . |
| Доказательство: |
| Предположим, что существует. Тогда, так как не содержит в себе сайтов и содержит на границе, . Отсюда выходит, что лежит — вершина или лежит на ребре диаграммы. Но по предыдущей лемме выходит, что не может быть вершиной диаграммы. Значит, она лежит на ребре, заданном серединным перпендикуляром к . Докажем в другую сторону: пусть серединный перпендикуляр к задаёт ребро диаграммы. Наибольшая пустая окружность любой точки на этом ребре должна содержать на границе и , и никаких других сайтов внутри. |
| Теорема: |
Если соединить все сайты, соответствующие смежным ячейкам диаграммы Вороного, получится триангуляция Делоне для этого множества точек. |
| Доказательство: |
| Если ячейки, соответствующие сайтам , смежны, то серединный перпендикуляр к отрезку образует ребро диаграммы Вороного, то есть к нему применима предыдущая лемма и можно построить окружность с и на границе, внутри которой не будет других сайтов. Триангуляции Делоне принадлежат те и только те рёбра (с поправкой на точки, лежащие на одной окружности), на которых можно построить такую окружность, что внутри неё не будет лежать никаких точек. Тогда ребро является ребром триангуляции Делоне. За счёт равносильности в обеих используемых леммах мы добавим все рёбра и не построим лишних. |
Построение
Наивный алгоритм
Будем пересекать полуплоскости по по свойству ячейки диаграммы. Необходимо раз пересечь плоскость, что суммарно делается за .
Инкрементальный алгоритм
Храним диаграмму в РСДС. Пусть у нас уже есть диаграмма для точек . Добавим новый сайт . Сначала найдём сайт , в ячейку которого попадает . После этого строим новую ячейку: сначала проведём серединный перпендикуляр для , он пересечёт границу ячейки с ячейкой ; на следующем шаге будем строить серединный перпендикуляр для и так далее.
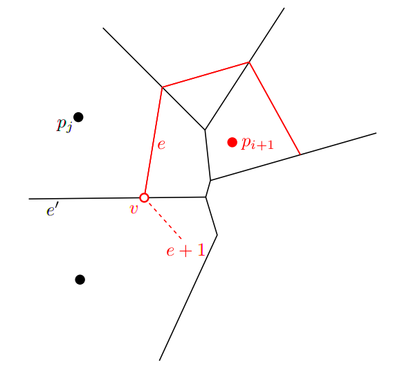
В процессе построения перпендикуляров необходимо обновлять РСДС. Каждый раз, когда новое ребро , порождаемое и , пересекает существовавшее ранее ребро , создаётся новая вершина и начинается новое ребро .
Обновление РСДС происходит следующим образом:
- создаём вершину с ребром ;
- для ребра в РСДС второй конец в вершине , следующее ребро — , инцидентные грани — слева , справа — ;
- добавляем в РСДС ребро с началом в и предыдущим ребром ;
- удаляем все рёбра, лежащие между вершиной начала и вершиной конца , по часовой стрелке;
- обновляем ребро, соответствующее грани для — им становится .
Каждый шаг выполняется за , значит, суммарно диаграмма из сайтов с нуля создаётся за .
Диаграмма -го порядка
Ячейка Вороного -го порядка — множество точек, имеющих в качестве ближайших соседей определённое множество из сайтов. Чтобы построить диаграмму -го порядка, нужно взять диаграмму -го порядка для первых сайтов и заменить каждую ячейку на диаграмму Вороного на множестве остальных сайтов.
Farthest-point диаграмма
Диаграмма -го порядка является farthest-point диаграммой, т.е. в каждой её ячейке все точки являются наиболее удалёнными от какого-то сайта.
| Утверждение: |
Сайт имеет ячейку в farthest-point диаграмме тогда и только тогда, когда он является вершиной выпуклой оболочки всех сайтов. |
| Утверждение: |
Все ячейки в farthest-point диаграмме неограничены. |
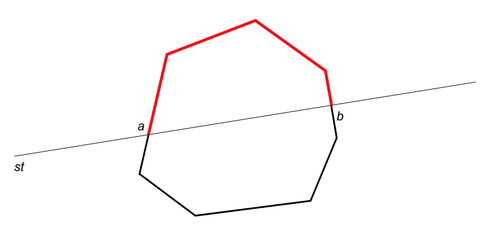
Чтобы найти farthest-point диаграмму, сначала найдём выпуклую оболочку всех сайтов. Обозначим сайты, её образующие, через . Делаем их случайную перестановку, но запомним порядки обхода в выпуклой оболочке по часовой стрелке () и против часовой (). Далее удаляем из выпуклой оболочки все точки, кроме первых трёх (запоминая при этом их соседей в оболочке на момент удаления). После этого мы строим farthest-point диаграмму для первых трёх точек и последовательно добавляем остальные (удалённые) в порядке, обратном порядку удаления.
Для точки ячейка встанет «между» ячейками, соответствующими и . Перед добавлением и — соседи, поэтому между ними построен серединный перпендикуляр. Серединный перпендикуляр к даст новое ребро, которое лежит в farthest-point ячейке и является частью границы ячейки . Обойдём ячейку по часовой стрелке, чтоб понять, какое ребро пересечёт перпендикуляр. С другой стороны этого ребра лежит ячейка какой-то точки , и серединный перпендикуляр тоже даст ребро ячейке . Аналогично совершим обход и так далее. Последний серединный перпендикуляр будет построен для . После этого удаляем рёбра, которые лежат внутри новой ячейки.
Источники
- de Berg, Cheong, van Kreveld, Overmars. Computational Geometry, Algorithms and Applicants, 2008. pp. 147-151, 164-166
- Инкрементальный алгоритм
- Wikipedia — Voronoi diagram
- Диаграммы высших порядков