Обсуждение участника:SergeyBud — различия между версиями
SergeyBud (обсуждение | вклад) |
SergeyBud (обсуждение | вклад) |
||
| (не показано 36 промежуточных версий 3 участников) | |||
| Строка 1: | Строка 1: | ||
| − | ''' | + | '''Формулировка задачи:''' По заданному слову <tex>X[0..m-1]</tex> найти в тексте или словаре <tex>Y[0..n-1]</tex> все слова, совпадающие с этим словом (или начинающиеся с этого слова) с учетом <tex>k</tex> возможных различий. |
| − | == | + | ==Описание задачи с точки зрения динамического программирования== |
| − | + | Пусть <tex>d_{i,j}</tex> - расстояние между префиксами строк <tex>x</tex> и <tex>y</tex>, длины которых равны, соответственно, <tex>i</tex> и <tex>j</tex>, то есть | |
| + | <tex>d_{i,j} = d(x(1,i), y(1,j))</tex>. | ||
| + | Чтобы решить задачу <tex>k</tex> различий, [[wikipedia:ru:Матрица_расстояний|матрицу расстояний]] надо преобразовать таким образом, чтобы <tex>d_{i,j}</tex> представлял минимальное расстояние между <tex>x(1, i)</tex> и любой подстрокой <tex>y</tex>, заканчивающейся символом <tex>y_j</tex>. Для этого достаточно ввести условие: | ||
| − | + | <tex>d_{0,j} = 0, 0 < j < n</tex> . | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Оставшуюся часть матрицы вычислим с использованием цен редактирования расстояния Левенштейна и рекуррентного соотношения для <tex>d_{i,j}</tex>: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | <tex>w(a,{\varepsilon}) = 1</tex> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <tex>w({\varepsilon}, b) = 1</tex> | |
| − | = | + | <tex>w(a, b) = \left\{\begin{array}{llcl} |
| − | + | 0&,\ a{\ne}b\\ | |
| − | + | 1&,\ a=b\\ | |
| + | \end{array}\right. | ||
| + | </tex> | ||
| − | == | + | <tex>d_{i,j} = min(d_{i-1,j} + w(x_i,{\varepsilon}), d_{i,j-1} + w({\varepsilon}, y_j), d_{i-1,j-1} + w(x_i, y_i))</tex> |
| − | + | ||
| − | + | Теперь каждое значение, не превосходящее <tex>k</tex>, в последней строке указывает позицию в тексте, в которой заканчивается строка, имеющая не больше <tex>k</tex> отличий от образца. | |
| + | ===Пример=== | ||
| + | Рассмотрим этот подход к решению задачи на примере: пусть <tex>X=ABCDE, Y=ACEABPCQDEABCR</tex>. Построим матрицу расстояний для этого случая: | ||
| + | [[Файл:Table_k_razlichiy.png]] | ||
| + | |||
| + | Последняя строка матрицы показывает, что вхождения образца с точностью до <tex>2</tex> отличий, заканчиваются в позициях <tex>3</tex>, <tex>10</tex>, <tex>13</tex> и <tex>14</tex>. Соответствующими подстроками являются <tex>ACE</tex>, <tex>ABPCQDE</tex>, <tex>ABC</tex> и <tex>ABCR</tex>. | ||
| + | |||
| + | ==Алгоритм== | ||
| + | |||
| + | [[Алгоритм_Укконена|Алгоритм Укконена]] говорит, что при вычисления расстояний между строками, диагонали матрицы можно пронумеровать целыми числами <tex>p {\in} [-m, n]</tex>, таким образом, чтобы диагональ <tex>p</tex> состояла из элементов <tex>(i, j)</tex>, у которых <tex>j - i = p</tex>. Пусть <tex>r_{p,q}</tex> представляет наибольшую строку <tex>i</tex>, у которой <tex>d_{i,j} = q</tex> и <tex>(i, j)</tex> лежит на диагонали <tex>p</tex>. Таким образом, <tex>q</tex> – это минимальное число различий между <tex>x(1, r_{p,q})</tex> и любой подстрокой текста, заканчивающейся <tex>y_{r_{p,q}+p}</tex>. Значение <tex>m</tex> в строке <tex>r_{p,q}</tex>, для <tex>q < k</tex>, указывает, что в тексте имеется вхождение образца с точностью до <tex>k</tex> отличий, заканчивающееся в <tex>y_{m+p}</tex>. Таким образом, чтобы решить задачу <tex>k</tex> различий, достаточно вычислить значения <tex>r_{p,q}</tex> для <tex>q < k</tex>. | ||
| + | |||
| + | Рассмотрим алгоритм вычисления <tex>r_{p,q}</tex>. | ||
| + | '''for''' p = 0 '''to''' n | ||
| + | r(p,-1) = -1 | ||
| + | '''for''' p = -(k+1) '''to''' -1 | ||
| + | r(p,|p|-1) = |p|-1 | ||
| + | r(p,|p|-2) = |p|-2 | ||
| + | '''for''' q = -1 '''to''' k | ||
| + | r(n+1,q) = -1 | ||
| + | '''for''' q = 0 '''to''' k | ||
| + | '''for''' p = -q '''to''' n | ||
| + | r = max(r(p,q-1) + 1, r(p-1,q-1), r(p+1,q-1) + 1) | ||
| + | r = min(r, m) | ||
| + | '''while''' r < m '''and''' r + p < n '''and''' x(r+1) = y(r+1+p) | ||
| + | r++ | ||
| + | r(p,q) = r | ||
| + | '''if''' r(p,q) = m | ||
| + | имеется вхождение с k отличиями, заканчивающееся в y(p+m) | ||
| + | Алгоритм вычисляет значения <tex>r_{p,q}</tex> на <tex>n+k+1</tex> диагоналях. Для каждой диагонали переменной строки <tex>r</tex> можно присвоить не больше <tex>m</tex> различных значений, что приводит к времени вычислений <tex>O(mn)</tex>. Рассмотрим как можно ускорить решение этой задачи, используя другие методы. | ||
| + | ===Предварительные вычисления=== | ||
| + | |||
| + | На этапе предварительной обработки, с помощью алгоритма Вейнера<ref>[http://europa.zbh.uni-hamburg.de/pubs/pdf/GieKur1997.pdf Giegerich R., Kurtz S. {{---}} From Ukkonen to McCreight and Weiner: A Unifying View of Linear-Time Suffix Tree Construction]</ref> строится [[wikipedia:ru:Суффиксное_дерево|суффиксное дерево]] строки <tex>y{\#}x{\$}</tex>, где <tex>\#</tex> и <tex>\$</tex> – символы, не принадлежащие алфавиту, над которыми построены строки <tex>x</tex> и <tex>y</tex>. Этот алгоритм требует линейных затрат памяти, и, для алфавита фиксированного размера, линейного времени. Для неограниченных алфавитов этот алфавит можно преобразовать так, что он будет выполняться за время <tex>O(n\log{\sigma})</tex>, где <tex>\sigma</tex> – число различающихся символов образца. Стадия предварительной обработки требует время <tex>O(n)</tex> и <tex>O(n\log{m})</tex> для постоянного и неограниченного алфавитов, соответственно. | ||
| + | ===Модификация предыдущего алгоритма=== | ||
| + | |||
| + | В приведенном выше алгоритме перед циклом <tex>while</tex> для диагонали <tex>p</tex>, переменной <tex>r</tex> было присвоено такое значение, что <tex>x(1, r)</tex> сопоставляется с точностью до <tex>k</tex> различий с некоторой подстрокой текста, заканчивающейся <tex>y_{r+p}</tex>. Тогда функция цикла <tex>while</tex> находит максимальное значение для которого <tex>x(r+1, r+h) = y(r+p+1, r+p+h)</tex>. Обозначим это значение как <tex>h</tex>. Это эквивалентно нахождению длины самого длинного общего префикса суффиксов <tex>x(r+1, m)\$</tex> и <tex>y(r+p+1,n){\#}x{\$}</tex> предварительно вычисленной конкатенированной строки. Символ <tex>\#</tex> используется для предотвращения ситуаций, в которых может ошибочно рассматриваться префикс, состоящий из символов как <tex>y</tex>, так и <tex>x</tex>. Обозначим <tex>lca(r,p)</tex> как самый низкий общий предок в суффиксном дереве с листьями, определенными вышеуказанными суффиксами, тогда нужное значение <tex>h</tex> задается <tex>length(lca(r,p))</tex>. | ||
| + | ===Оценка времени работы=== | ||
| + | |||
| + | Суффиксное дерево имеет <tex>O(n)</tex> узлов. Для поддержки определения самого низкого общего предка за линейное время, алгоритмам <tex>LCA</tex> требуется преобразование дерева, проводимое за линейное время. Значения <tex>r_{p,q}</tex> вычисляются на <tex>n+k+1</tex> диагоналях. Более того, для каждой диагонали надо вычислить <tex>k+1</tex> таких значений, что в общей сложности дает <tex>O(kn)</tex> запросов. Таким образом, общее время работы алгоритма k различий составляет <tex>O(kn)</tex> для алфавитов фиксированного размера, и <tex>O(n * \log{m} + kn)</tex> для неограниченных алфавитов. | ||
| + | ===Параллельная версия алгоритма=== | ||
| + | |||
| + | В 1989 году Ландау и Вишкин разработали параллельную версию алгоритма. Она позволяет уменьшить время работы до <tex>O(\log{n}+k)</tex>, при использовании одновременно <tex>n</tex> процессоров. Для данной оценки необходимо, чтобы каждый из процессоров выполнял последовательный запрос <tex>LCA</tex> за <tex>O(1)</tex>. | ||
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
| + | |||
| + | ==Источники информации== | ||
| + | * [http://algolist.manual.ru/search/fsearch/k_razl.php k-различий - алгоритм Ландау-Вишкина] | ||
Текущая версия на 20:22, 22 мая 2015
Формулировка задачи: По заданному слову найти в тексте или словаре все слова, совпадающие с этим словом (или начинающиеся с этого слова) с учетом возможных различий.
Содержание
Описание задачи с точки зрения динамического программирования
Пусть - расстояние между префиксами строк и , длины которых равны, соответственно, и , то есть . Чтобы решить задачу различий, матрицу расстояний надо преобразовать таким образом, чтобы представлял минимальное расстояние между и любой подстрокой , заканчивающейся символом . Для этого достаточно ввести условие:
.
Оставшуюся часть матрицы вычислим с использованием цен редактирования расстояния Левенштейна и рекуррентного соотношения для :
Теперь каждое значение, не превосходящее , в последней строке указывает позицию в тексте, в которой заканчивается строка, имеющая не больше отличий от образца.
Пример
Рассмотрим этот подход к решению задачи на примере: пусть . Построим матрицу расстояний для этого случая:
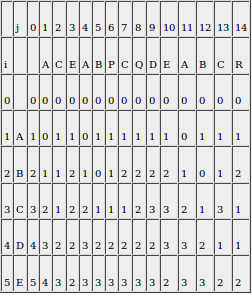
Последняя строка матрицы показывает, что вхождения образца с точностью до отличий, заканчиваются в позициях , , и . Соответствующими подстроками являются , , и .
Алгоритм
Алгоритм Укконена говорит, что при вычисления расстояний между строками, диагонали матрицы можно пронумеровать целыми числами , таким образом, чтобы диагональ состояла из элементов , у которых . Пусть представляет наибольшую строку , у которой и лежит на диагонали . Таким образом, – это минимальное число различий между и любой подстрокой текста, заканчивающейся . Значение в строке , для , указывает, что в тексте имеется вхождение образца с точностью до отличий, заканчивающееся в . Таким образом, чтобы решить задачу различий, достаточно вычислить значения для .
Рассмотрим алгоритм вычисления .
for p = 0 to n
r(p,-1) = -1
for p = -(k+1) to -1
r(p,|p|-1) = |p|-1
r(p,|p|-2) = |p|-2
for q = -1 to k
r(n+1,q) = -1
for q = 0 to k
for p = -q to n
r = max(r(p,q-1) + 1, r(p-1,q-1), r(p+1,q-1) + 1)
r = min(r, m)
while r < m and r + p < n and x(r+1) = y(r+1+p)
r++
r(p,q) = r
if r(p,q) = m
имеется вхождение с k отличиями, заканчивающееся в y(p+m)
Алгоритм вычисляет значения на диагоналях. Для каждой диагонали переменной строки можно присвоить не больше различных значений, что приводит к времени вычислений . Рассмотрим как можно ускорить решение этой задачи, используя другие методы.
Предварительные вычисления
На этапе предварительной обработки, с помощью алгоритма Вейнера[1] строится суффиксное дерево строки , где и – символы, не принадлежащие алфавиту, над которыми построены строки и . Этот алгоритм требует линейных затрат памяти, и, для алфавита фиксированного размера, линейного времени. Для неограниченных алфавитов этот алфавит можно преобразовать так, что он будет выполняться за время , где – число различающихся символов образца. Стадия предварительной обработки требует время и для постоянного и неограниченного алфавитов, соответственно.
Модификация предыдущего алгоритма
В приведенном выше алгоритме перед циклом для диагонали , переменной было присвоено такое значение, что сопоставляется с точностью до различий с некоторой подстрокой текста, заканчивающейся . Тогда функция цикла находит максимальное значение для которого . Обозначим это значение как . Это эквивалентно нахождению длины самого длинного общего префикса суффиксов и предварительно вычисленной конкатенированной строки. Символ используется для предотвращения ситуаций, в которых может ошибочно рассматриваться префикс, состоящий из символов как , так и . Обозначим как самый низкий общий предок в суффиксном дереве с листьями, определенными вышеуказанными суффиксами, тогда нужное значение задается .
Оценка времени работы
Суффиксное дерево имеет узлов. Для поддержки определения самого низкого общего предка за линейное время, алгоритмам требуется преобразование дерева, проводимое за линейное время. Значения вычисляются на диагоналях. Более того, для каждой диагонали надо вычислить таких значений, что в общей сложности дает запросов. Таким образом, общее время работы алгоритма k различий составляет для алфавитов фиксированного размера, и для неограниченных алфавитов.
Параллельная версия алгоритма
В 1989 году Ландау и Вишкин разработали параллельную версию алгоритма. Она позволяет уменьшить время работы до , при использовании одновременно процессоров. Для данной оценки необходимо, чтобы каждый из процессоров выполнял последовательный запрос за .