Сортировка слиянием — различия между версиями
Ильнар (обсуждение | вклад) |
Ильнар (обсуждение | вклад) (→См. также) |
||
| Строка 80: | Строка 80: | ||
* [[Сортировка кучей]] | * [[Сортировка кучей]] | ||
* [[Быстрая сортировка]] | * [[Быстрая сортировка]] | ||
| + | * [[Timsort]] | ||
*[[Cортировка слиянием с использованием O(1) дополнительной памяти]] | *[[Cортировка слиянием с использованием O(1) дополнительной памяти]] | ||
Версия 15:11, 23 мая 2015
Сортировка слиянием (англ. Merge sort) — алгоритм сортировки, предложенный Джоном фон Нейманом в 1945 году.
Это устойчивый алгоритм, использующий дополнительной памяти и работающий за времени.
Содержание
Принцип работы
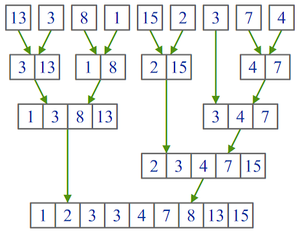
Алгоритм использует принцип «разделяй и властвуй»: задача разбивается на подзадачи меньшего размера, которые решаются по отдельности, после чего их решения комбинируются для получения решения исходной задачи. Конкретно процедуру сортировки слиянием можно описать следующим образом:
- Если в рассматриваемом массиве один элемент, то он уже отсортирован — алгоритм завершает работу.
- Иначе массив разбивается на две части, которые сортируются рекурсивно.
- После сортировки двух частей массива к ним применяется процедура слияния, которая по двум отсортированным частям получает исходный отсортированный массив.
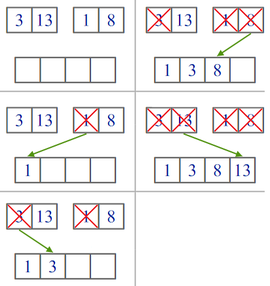
Слияние двух массивов
У нас есть два массива и (фактически это будут две части одного массива, но для удобства будем писать, что у нас просто два массива). Нам надо получить массив размером . Для этого можно применить процедуру слияния. Эта процедура заключается в том, что мы сравниваем элементы массивов (начиная с начала) и меньший из них записываем в финальный. И затем, в массиве у которого оказался меньший элемент, переходим к следующему элементу и сравниваем теперь его. В конце, если один из массивов закончился, мы просто дописываем в финальный другой массив. После мы наш финальный массив записываем заместо двух исходных и получаем отсортированный участок.
Множество отсортированных списков с операцией является моноидом, , где — нейтральный элемент.
Ниже приведён псевдокод процедуры слияния, который сливает две части массива — и
function merge(a : int[n]; left, mid, right : int):
it1 = 0
it2 = 0
result : int[right - left]
while left + it1 < mid and mid + it2 < right
if a[left + it1] < a[mid + it2]
result[it1 + it2] = a[left + it1]
it1 += 1
else
result[it1 + it2] = a[mid + it2]
it2 += 1
while left + it1 < mid
result[it1 + it2] = a[left + it1]
it1 += 1
while mid + it2 < right
result[it1 + it2] = a[mid + it2]
it2 += 1
for i = 0 to it1 + it2
a[left + i] = result[i]
Рекурсивный алгоритм
Функция сортирует подотрезок массива с индексами в полуинтервале .
function mergeSortRecursive(a : int[n]; left, right : int):
if left + 1 >= right
return
mid = (left + right) / 2
mergeSortRecursive(a, left, mid)
mergeSortRecursive(a, mid, right)
merge(a, left, mid, right)
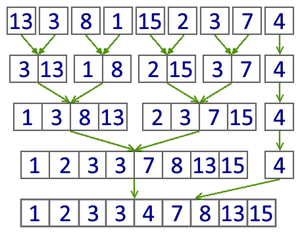
Итеративный алгоритм
При итеративном алгоритме не происходит рекурсивного запуска, что сохранит памяти, которое отдавалось для стека вызовов.
function mergeSortIterative(a : int[n]):
for i = 1 to n, i *= 2
for j = 0 to n - i, j += 2 * i
merge(a, j, j + i, min(j + 2 * i, n))
Время работы
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай — время сортировки массива длины , тогда для сортировки слиянием справедливо
— время, необходимое на то, чтобы слить два массива. Распишем это соотношение:
.
Осталось оценить . Мы знаем, что , а значит . Уравнение примет вид . Так как — константа, то .
Достоинства:
- устойчивая.
Недостатки:
- при любых входных данных время работы — ,
- требуется дополнительно памяти.
См. также
- Сортировка кучей
- Быстрая сортировка
- Timsort
- Cортировка слиянием с использованием O(1) дополнительной памяти