Динамическая выпуклая оболочка (достаточно log^2 на добавление/удаление) — различия между версиями
(→Вставка точки) |
(→Вставка точки: подправлены О-шки) |
||
| (не показана 1 промежуточная версия 1 участника) | |||
| Строка 1: | Строка 1: | ||
| − | Пусть дано множество точек <tex>S</tex>, изначально пустое, и | + | Пусть дано множество точек <tex>S</tex>, изначально пустое, и набор точек <tex>\{p_i\}^n_{i = 1}</tex>, которые последовательно добавляются или удаляются из <tex>S</tex> (естественно, точка может быть удалена, если она уже принадлежит <tex>S</tex>). Требуется динамически поддерживать выпуклую оболочку <tex>S</tex>. |
В статье описан алгоритм, требующий <tex>O(\log^2{n})</tex> времени на добавление/удаление точки. | В статье описан алгоритм, требующий <tex>O(\log^2{n})</tex> времени на добавление/удаление точки. | ||
| Строка 34: | Строка 34: | ||
== Объединение двух выпуклых оболочек == | == Объединение двух выпуклых оболочек == | ||
| − | Теперь, когда отсортированные точки хранятся в структуре, поддерживающей эффективный поиск, мы можем воспользоватся идеями бинарного поиска для нахождения моста. Для этого необходим критерий спуска, по которому мы будем определять подотрезок, до которого нужно сузить задачу, имея точки <tex>p</tex> и <tex>q</tex>, определяющие секущую к выпуклым оболочкам множеств <tex>A</tex> и <tex>C</tex> . | + | Теперь, когда отсортированные точки хранятся в структуре, поддерживающей эффективный поиск, мы можем воспользоватся идеями [[Целочисленный двоичный поиск|бинарного поиска]] для нахождения моста. Для этого необходим критерий спуска, по которому мы будем определять подотрезок, до которого нужно сузить задачу, имея точки <tex>p</tex> и <tex>q</tex>, определяющие секущую к выпуклым оболочкам множеств <tex>A</tex> и <tex>C</tex> . |
Рассмотрим дополнительно 4 точки: | Рассмотрим дополнительно 4 точки: | ||
| − | <tex>p^{+}</tex> - следующая за <tex>p</tex> точка выпуклой оболочки множества <tex>A</tex> в отсортированном порядке, то есть <tex>p_{y}^{+} > p_{y}</tex> и ордината <tex>p_{y}</tex> - наименьшая. | + | <tex>p^{+}</tex> {{---}} следующая за <tex>p</tex> точка выпуклой оболочки множества <tex>A</tex> в отсортированном порядке, то есть <tex>p_{y}^{+} > p_{y}</tex> и ордината <tex>p_{y}</tex> {{---}} наименьшая. |
| − | <tex>p^{-}</tex> - предыдущая <tex>p</tex> точка выпуклой оболочки множества <tex>A</tex> в отсортированном порядке, то есть <tex>p_{y}^{-} < p_{y}</tex> и ордината <tex>p_{y}</tex> - наибольшая. | + | <tex>p^{-}</tex> {{---}} предыдущая <tex>p</tex> точка выпуклой оболочки множества <tex>A</tex> в отсортированном порядке, то есть <tex>p_{y}^{-} < p_{y}</tex> и ордината <tex>p_{y}</tex> {{---}} наибольшая. |
| − | <tex>q^{+}</tex> - следующая за <tex>q</tex> точка выпуклой оболочки множества <tex>C</tex> в отсортированном порядке, то есть <tex>q_{y}^{+} > q_{y}</tex> и ордината <tex>q_{y}</tex> - наименьшая. | + | <tex>q^{+}</tex> {{---}} следующая за <tex>q</tex> точка выпуклой оболочки множества <tex>C</tex> в отсортированном порядке, то есть <tex>q_{y}^{+} > q_{y}</tex> и ордината <tex>q_{y}</tex> {{---}} наименьшая. |
| − | <tex>q^{-}</tex> - предыдущая <tex>q</tex> точка выпуклой оболочки множества <tex>C</tex> в отсортированном порядке, то есть <tex>q_{y}^{-} < q_{y}</tex> и ордината <tex>q_{y}</tex> - наибольшая. | + | <tex>q^{-}</tex> {{---}} предыдущая <tex>q</tex> точка выпуклой оболочки множества <tex>C</tex> в отсортированном порядке, то есть <tex>q_{y}^{-} < q_{y}</tex> и ордината <tex>q_{y}</tex> {{---}} наибольшая. |
Тогда в зависимости от взаимного расположения вектора <tex>\overrightarrow{qp}</tex> и точек <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex>, <tex>q^{-}</tex> можно определить, какой из 9 случаев рассматривать, а именно: | Тогда в зависимости от взаимного расположения вектора <tex>\overrightarrow{qp}</tex> и точек <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex>, <tex>q^{-}</tex> можно определить, какой из 9 случаев рассматривать, а именно: | ||
| − | a) Все точки <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex>, <tex>q^{-}</tex> расположены справа от вектора <tex>\overrightarrow{qp}</tex> ( | + | :a) Все точки <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex>, <tex>q^{-}</tex> расположены справа от вектора <tex>\overrightarrow{qp}</tex> (точка <tex>t</tex> находится слева (справа) от вектора <tex>\overrightarrow{qp}</tex>, если [[Предикат "левый поворот"|предикат "левый поворот"]] для точек <tex>q</tex>, <tex>p</tex>, <tex>t</tex> положительный (отрицательный)) {{---}} найден мост. |
| − | b) <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex> - справа, <tex>q^{-}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :b) <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{+}</tex> {{---}} справа, <tex>q^{-}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
| − | c) <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{-}</tex> - справа, <tex>q^{+}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :c) <tex>p^{+}</tex>, <tex>p^{-}</tex>, <tex>q^{-}</tex> {{---}} справа, <tex>q^{+}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
| − | d) Как в случае b, только слева от <tex>\overrightarrow{qp}</tex> находится точка <tex>p^{+}</tex> | + | :d) Как в случае b, только слева от <tex>\overrightarrow{qp}</tex> находится точка <tex>p^{+}</tex> |
| − | e) Как в случае c, только слева от <tex>\overrightarrow{qp}</tex> находится точка <tex>p^{-}</tex> | + | :e) Как в случае c, только слева от <tex>\overrightarrow{qp}</tex> находится точка <tex>p^{-}</tex> |
| − | f) <tex>p^{-}</tex>, <tex>q^{+}</tex> - справа, <tex>p^{+}</tex>, <tex>q^{-}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :f) <tex>p^{-}</tex>, <tex>q^{+}</tex> {{---}} справа, <tex>p^{+}</tex>, <tex>q^{-}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
| − | g) <tex>p^{+}</tex>, <tex>q^{+}</tex> - справа, <tex>p^{-}</tex>, <tex>q^{-}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :g) <tex>p^{+}</tex>, <tex>q^{+}</tex> {{---}} справа, <tex>p^{-}</tex>, <tex>q^{-}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
| − | h) <tex>p^{-}</tex>, <tex>q^{-}</tex> - справа, <tex>p^{+}</tex>, <tex>q^{+}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :h) <tex>p^{-}</tex>, <tex>q^{-}</tex> {{---}} справа, <tex>p^{+}</tex>, <tex>q^{+}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
| − | i) <tex>p^{+}</tex>, <tex>q^{-}</tex> - справа, <tex>p^{-}</tex>, <tex>q^{+}</tex> - слева от <tex>\overrightarrow{qp}</tex> | + | :i) <tex>p^{+}</tex>, <tex>q^{-}</tex> {{---}} справа, <tex>p^{-}</tex>, <tex>q^{+}</tex> {{---}} слева от <tex>\overrightarrow{qp}</tex> |
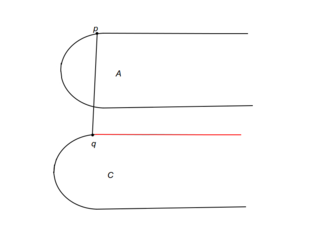
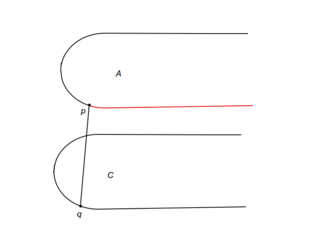
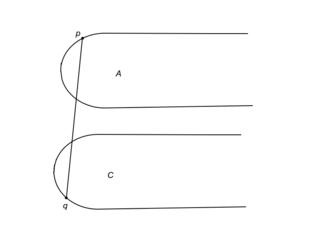
Для случаев a-h на картинках красным показано, какие части выпуклых оболочек могут быть отброшены. Случай же i немного сложнее. | Для случаев a-h на картинках красным показано, какие части выпуклых оболочек могут быть отброшены. Случай же i немного сложнее. | ||
| Строка 89: | Строка 89: | ||
|} | |} | ||
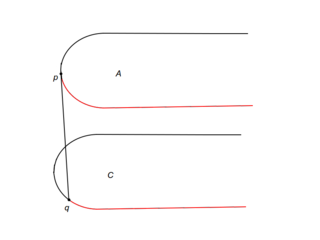
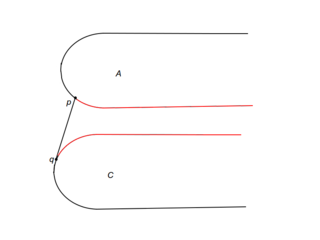
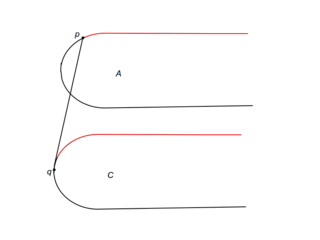
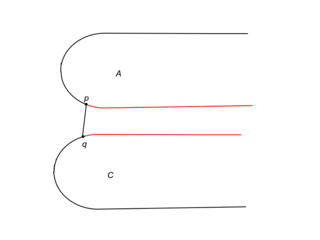
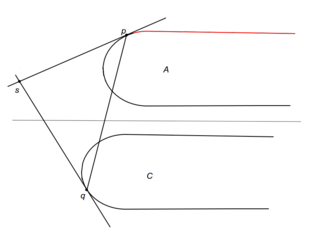
| − | Рассмотрим подробно случай i. Пусть <tex>m</tex> {{---}} прямая, разбивающая <tex>P</tex> на <tex>A</tex> и <tex>C</tex>. Пусть также <tex>l_p</tex> и <tex>l_q</tex> {{---}} касательные к выпуклым оболочкам в точках <tex>p</tex> и <tex>q</tex> соответственно. Если <tex>s</tex> {{---}} точка пересечения <tex>l_p</tex> и <tex>l_q</tex> лежит ниже прямой <tex>m</tex>, то точка пересечения моста и выпуклой оболочки <tex>A</tex> может лежать в треугольнике, образованном прямыми <tex>l_p</tex>, <tex>l</tex> и <tex>m</tex>, или выше <tex>p</tex>. Тогда можем удалить часть <tex>C</tex> ниже <tex>q</tex>. Случай, когда <tex>s</tex> лежит выше <tex>m</tex>, аналогичен (см. рис.). | + | Рассмотрим подробно случай i. Пусть <tex>m</tex> {{---}} прямая, разбивающая <tex>P</tex> на <tex>A</tex> и <tex>C</tex>. Пусть также <tex>l_p</tex> и <tex>l_q</tex> {{---}} касательные к выпуклым оболочкам в точках <tex>p</tex> и <tex>q</tex> соответственно. Если <tex>s</tex> {{---}} точка пересечения <tex>l_p</tex> и <tex>l_q</tex> лежит ниже прямой <tex>m</tex>, то точка пересечения моста и выпуклой оболочки <tex>A</tex> может лежать в треугольнике, образованном прямыми <tex>l_p</tex>, <tex>l</tex> и <tex>m</tex>, или выше <tex>p</tex>. Тогда можем удалить часть <tex>C</tex> ниже <tex>q</tex> (см. рис. i1). Случай, когда <tex>s</tex> лежит выше <tex>m</tex>, аналогичен (см. рис. i2). |
{|border="0" cellpadding="5" width=30% align=center | {|border="0" cellpadding="5" width=30% align=center | ||
| Строка 144: | Строка 144: | ||
=== Вставка точки === | === Вставка точки === | ||
| − | Вставим точку в дерево, как в обычное сбалансированное дерево поиска. После этого необходимо пересчитать мосты для некоторых вершин дерева. В вершине необходимо пересчитать мост, либо если в его поддерево была вставлена вершина, либо если при балансировке в повороте эта вершина была задействована (таких вершин <tex>O( | + | Вставим точку в дерево, как в обычное сбалансированное дерево поиска. После этого необходимо пересчитать мосты для некоторых вершин дерева. В вершине необходимо пересчитать мост, либо если в его поддерево была вставлена вершина, либо если при балансировке в повороте эта вершина была задействована (таких вершин <tex>O(\log{n})</tex>. Мосты в таких вершинах будем пересчитывать при подъеме по дереву после вставки вершины. Глубина дерева <tex>O(\log{n})</tex>, значит в процессе подъема будут пересчитаны мосты у <tex>O(\log{n})</tex> вершин. Каждый пересчет моста требует <tex>O(\log{n})</tex> времени, откуда итоговая асимптотика вставки: <tex>O(\log^2{n})</tex>. |
=== Удаление точки === | === Удаление точки === | ||
Текущая версия на 20:01, 26 мая 2015
Пусть дано множество точек , изначально пустое, и набор точек , которые последовательно добавляются или удаляются из (естественно, точка может быть удалена, если она уже принадлежит ). Требуется динамически поддерживать выпуклую оболочку .
В статье описан алгоритм, требующий времени на добавление/удаление точки.
Содержание
Левая и правая выпуклые оболочки
Определим левую (правую) выпуклую оболочку множества точек , как выпуклую оболочку множества , где . Тогда задачу можно свести к поддержанию отдельно левой и правой выпуклых оболочек. Будем рассматривать только динамическое поддержание левой оболочки (далее, для краткости, будем называть её просто выпуклой оболочкой). Заметим также, что точки вдоль выпуклой оболочки отсортированы по ординате.
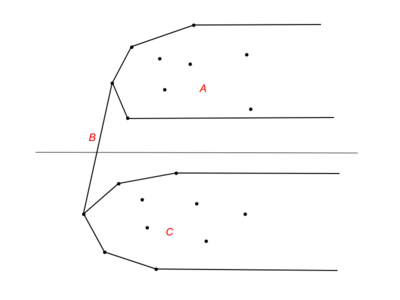
Пусть множество точек разбито горизонтальной прямой на два множества и . Рассмотрим выпуклые оболочки и . Будем называть мостом (bridge) отрезок общей касательной к этим оболочкам, заключённый между точками касания. Тогда выпуклая оболочка ко всему множеству естественным образом получается объединением частей оболочек и , и моста .
Основная идея алгоритма заключается в эффективном (за ) отыскании моста, соединяющего две такие оболочки.
Структура данных
Будем хранить отсортированные лексикографически () точки в листьях сбалансированного бинарного дерева поиска (например, красно-черного или AVL). Во внутренних вершинах будем хранить вспомогательную информацию: во-первых, наименьшую точку в поддереве с корнем в данной вершине; а во-вторых, мост между выпуклыми оболочками точек левого и правого поддеревьев данной вершины. Формально вершина дерева описывается так:
struct bridge point left point right
struct node
node parent, left, right
boolean leaf // true, если лист, иначе false
bridge b // поле валидно для внутренней вершины
point p // если вершина лист, то точка, хранящаяся в этом листе,
// иначе наименьшая точка в поддереве с корнем в данной вершине
Объединение двух выпуклых оболочек
Теперь, когда отсортированные точки хранятся в структуре, поддерживающей эффективный поиск, мы можем воспользоватся идеями бинарного поиска для нахождения моста. Для этого необходим критерий спуска, по которому мы будем определять подотрезок, до которого нужно сузить задачу, имея точки и , определяющие секущую к выпуклым оболочкам множеств и .
Рассмотрим дополнительно 4 точки:
— следующая за точка выпуклой оболочки множества в отсортированном порядке, то есть и ордината — наименьшая.
— предыдущая точка выпуклой оболочки множества в отсортированном порядке, то есть и ордината — наибольшая.
— следующая за точка выпуклой оболочки множества в отсортированном порядке, то есть и ордината — наименьшая.
— предыдущая точка выпуклой оболочки множества в отсортированном порядке, то есть и ордината — наибольшая.
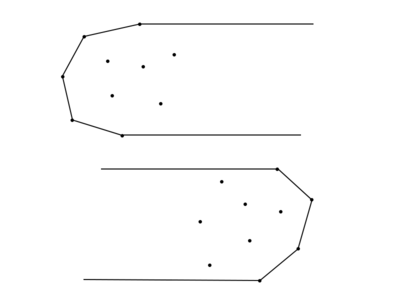
Тогда в зависимости от взаимного расположения вектора и точек , , , можно определить, какой из 9 случаев рассматривать, а именно:
- a) Все точки , , , расположены справа от вектора (точка находится слева (справа) от вектора , если предикат "левый поворот" для точек , , положительный (отрицательный)) — найден мост.
- b) , , — справа, — слева от
- c) , , — справа, — слева от
- d) Как в случае b, только слева от находится точка
- e) Как в случае c, только слева от находится точка
- f) , — справа, , — слева от
- g) , — справа, , — слева от
- h) , — справа, , — слева от
- i) , — справа, , — слева от
Для случаев a-h на картинках красным показано, какие части выпуклых оболочек могут быть отброшены. Случай же i немного сложнее.
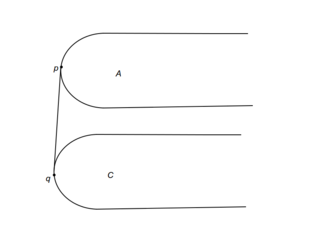
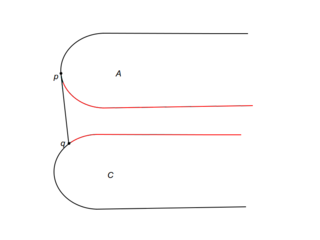
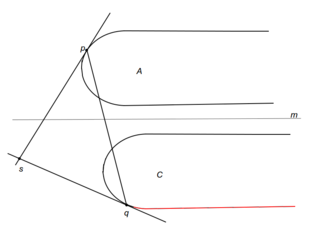
Рассмотрим подробно случай i. Пусть — прямая, разбивающая на и . Пусть также и — касательные к выпуклым оболочкам в точках и соответственно. Если — точка пересечения и лежит ниже прямой , то точка пересечения моста и выпуклой оболочки может лежать в треугольнике, образованном прямыми , и , или выше . Тогда можем удалить часть ниже (см. рис. i1). Случай, когда лежит выше , аналогичен (см. рис. i2).
Итак, на каждом шаге, мы или нашли ответ, или уменьшили размер и/или в два раза, следовательно нахождение моста работает за .
Объединение левой и правой выпуклой оболочки
Выписываем в порядке обхода вершины из левой выпуклой оболочки, затем выписываем с конца вершины из правой выпуклой оболочки. У них может оказаться от одной до двух общих вершин на концах (две в случае горизонтального ребра снизу/сверху), эта проблема решается путем извлечения "совпадающих" точек в момент обратного обхода правой выпуклой оболочки.
Операции
Получение выпуклой оболочки
Научимся восстанавливать выпуклую оболочку по дереву, описанному выше. Для этого рассмотрим более общую задачу: для данной вершины дерева и отрезка найти часть выпуклой оболочки, состоящей из точек поддерева с корнем в , ординаты которых лежат в этом отрезке. Это можно сделать следующим обходом:
get_hull(answer, v, l, r)
if (v.leaf)
return
a = v.bridge.left.y
b = v.bridge.right.y
if (l < a)
get_hull(answer, v.left, l, min(a, r))
if (l <= a and b <= r)
if (answer.empty())
answer = answer ++ v.bridge.left
answer = answer ++ v.bridge.right
if (b < r)
get_hull(answer, v.right, max(l, b), r)
Левый конец моста добавляется только если ответ пустой, иначе он уже был добавлен как правый конец другого моста. Чтобы получить выпуклую оболочку нужно вызвать get_hull([], root, , ).
Принадлежность точки выпуклой оболочке
По аналогии с предыдущим пунктом, сведем запрос к более общему запросу: для данной вершины дерева и отрезка проверить, принадлежит ли точка части выпуклой оболочки, состоящей из точек поддерева с корнем в , ординаты которых лежат в этом отрезке. Тогда принадлежность точки проверяется вызовом in_hull(p, root, , )
in_hull(p, v, l, r)
if (v.leaf)
return false
a = v.bridge.left.y
b = v.bridge.right.y
if (l <= a and b <= r)
if (v.bridge.left == p or v.bridge.right == p)
return true
if (l < a and p.y < a)
return in_hull(p, v.left, l, min(a, r))
if (b < r and b < p.y)
return in_hull(p, v.right, max(l, b), r)
return false
Вставка точки
Вставим точку в дерево, как в обычное сбалансированное дерево поиска. После этого необходимо пересчитать мосты для некоторых вершин дерева. В вершине необходимо пересчитать мост, либо если в его поддерево была вставлена вершина, либо если при балансировке в повороте эта вершина была задействована (таких вершин . Мосты в таких вершинах будем пересчитывать при подъеме по дереву после вставки вершины. Глубина дерева , значит в процессе подъема будут пересчитаны мосты у вершин. Каждый пересчет моста требует времени, откуда итоговая асимптотика вставки: .
Удаление точки
Удаление точки производится по аналогии с вставкой: сначала мы удалим точку из сбалансированного дерева поиска, а затем пересчитаем мосты, хранящиеся в вершинах, которые затронула балансировка. Очевидно, что удаление, как и вставка, работает за .
Источники
- Реализация Антона Ковшарова
- Ф. Препарата, М. Шеймос. Вычислительная геометрия (1989). стр. 151 (тут описан более сложный алгоритм с двухуровневой структурой данных, но с такой же асимптотикой)
- Overmars, M. H.; van Leeuwen, J. (1981), "Maintenance of configurations in the plane" (и тут тоже)