Поиск с помощью золотого сечения

Поиск с помощью золотого сечения (Golden section search) — это улучшение наивной реализации троичного поиска, служащего для нахождения минимума/максимума функции. При простом троичном поиске на каждой итерации функция вычисляется в двух точках. Метод же золотого сечения требует вычисления лишь в одной точке (за исключением первой итерации). За счет этого достигается выигрыш в производительности.

Алгоритм

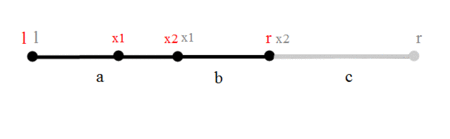
Рассмотрим одну итерацию алгоритма троичного поиска. Попробуем подобрать такое разбиение отрезка на три части, чтобы на следующей итерации одна из точек нового разбиения совпала с одной из точек текущего разбиения. Тогда в следующий раз не придется считать функцию в двух точках, так как в одной она уже была посчитана.

Потребуем, чтобы одновременно выполнялось:

[math] \dfrac{a + b}{c} = \dfrac{b + c}{a} = \varphi [/math]

[math] \dfrac{a}{b} = \varphi [/math]

[math] \dfrac{c}{b} = \varphi [/math]

Где [math] \varphi [/math] — это некоторое отношение, в котором мы делим отрезок (точки [math]x_1[/math] и [math]x_2[/math] разбивают отрезок симметрично).

Тогда:

[math] a + b = \varphi c, a = \varphi b, c = \varphi b[/math], откуда получаем [math] \varphi + 1 = \varphi^2 \Rightarrow \varphi = \dfrac{1 + \sqrt{5}}{2}[/math]   (тот корень уравнения, который меньше нуля, по понятным причинам отбросили).

Это число совпадает с золотым сечением. Отсюда название метода.

Для реализации алгоритма нам потребуется найти [math] a [/math] и [math] a + b [/math]. Если [math] L [/math] - длина исследуемого отрезка, тогда:

[math] \left(\dfrac{b + c}{a} = \varphi;\; b + c = L - a \right) \Rightarrow[/math]

[math] a = \dfrac{L}{\varphi + 1} [/math]

[math] a + b = L - c = L - a = L - \dfrac{L}{\varphi + 1}[/math]

Причем, заметим что в силу того что [math]\varphi[/math] — золотое сечение, то [math]\dfrac{1}{\varphi + 1} = 2 - \varphi[/math].

Формально для поиска минимума (для максимума — делается аналогично) функции [math] f [/math] делаем следующее:

Шаг 1:

Определяем границы поиска [math]l[/math] и [math]r[/math], затем устанавливаем текущее разбиение:

[math]x_1 = l + \dfrac{r - l}{\varphi + 1}[/math]

[math]x_2 = r - \dfrac{r - l}{\varphi + 1}[/math]

и вычислим функцию на них: [math]f_1 = f(x_1), f_2 = f(x_2)[/math]

Шаг 2:

если [math]f_1 \lt f_2[/math], тогда

[math]r = x_2[/math]

[math]x_2 = x_1, f_2 = f_1[/math]

[math]x_1 = l + \dfrac{r - l}{\varphi + 1},\; f_1 = f(x_1)[/math]

иначе:

[math]l = x_1[/math]

[math]x_1 = x_2, f_1 = f_2[/math]

[math]x_2 = r - \dfrac{r - l}{\varphi + 1},\; f_2 = f(x_2)[/math]

Шаг 3:

если точность [math]|r - l| \lt \varepsilon[/math] нас устраивает, тогда останавливаемся, и искомая точка [math]x = \dfrac{l + r}{2}[/math], иначе назад к шагу 2

Псевдокод

phi = (1 + sqrt(5)) / 2
resphi = 2 - phi

goldenSectionSearch(f, l, r, eps)
   x1 = l + resphi * (r - l)
   x2 = r - resphi * (r - l)
   f1 = f(x1)
   f2 = f(x2)
   
   do
       if f1 < f2:
           r = x2
           x2 = x1
           f2 = f1
           x1 = l + resphi * (r - l)
           f1 = f(x1)
       else:
           l = x1
           x1 = x2
           f1 = f2
           x2 = r - resphi * (r - l)
           f2 = f(x2)
   while abs(r - l) > eps
   
   return (x1 + x2) / 2

Время работы

Так как на каждой итерации мы считаем одно значение функции и уменьшаем область поиска в [math] \varphi [/math] раз, пока [math] r - l \gt \varepsilon[/math], то время работы алгоритма составит [math] \log_{\varphi}\left(\dfrac{r - l}{\varepsilon}\right)[/math].

Если удельный вес вычисления функции [math] f [/math] достаточно большой, тогда получим ускорение работы примерно в 2,4 раз по сравнению с неулучшенным троичным поиском ([math] \log_{\varphi}\left(\dfrac{r - l}{\varepsilon}\right)[/math] против [math]2 \log_{\dfrac32} \left(\dfrac{r - l}{\varepsilon}\right)[/math].

См также

• Троичный поиск

Ссылки

• Википедия - Метод золотого сечения

• Wikipedia - Golden section search (english)