|
|
| Строка 1: |
Строка 1: |
| | ==Постановка задачи== | | ==Постановка задачи== |
| − | Даны матроиды <tex>M_1 = (S, I_1)</tex> и <tex>M_2 = (S, I_2)</tex>. Необходимо найти максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex> | + | Даны матроиды <tex>M_1 = \langle S, I_1 \rangle</tex> и <tex>M_2 = \langle S, I_2 \rangle</tex>. Необходимо найти максимальное по мощности независимое множество в пересечении <tex>M_1</tex> и <tex>M_2</tex> |
| | | | |
| | ==Алгоритм решения== | | ==Алгоритм решения== |
Версия 17:56, 6 июня 2015
Постановка задачи
Даны матроиды [math]M_1 = \langle S, I_1 \rangle[/math] и [math]M_2 = \langle S, I_2 \rangle[/math]. Необходимо найти максимальное по мощности независимое множество в пересечении [math]M_1[/math] и [math]M_2[/math]
Алгоритм решения
Пусть множество [math]J \in (I_1 \cap I_2)[/math]
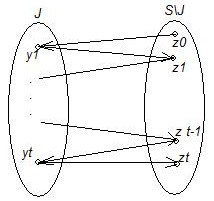
Определим граф замен [math]D_{M_1, M_2}(J) = (S, A(J))[/math], где
[math]A(J) = \{(y, z) | y \in J, z \in S\setminus J, J - y + z \in I_1 \} [/math]
[math]\cup \{ (z', y') | z' \in S \setminus J, y' \in J, J - y' + z' \in I_2 \}[/math]
Пусть [math]X_1 = \{ z \in S \setminus J | J + z \in I_1 \}[/math], [math]X_2 = \{ z \in S \setminus J | J + z \in I_2 \}[/math], [math]P[/math] - кратчайший путь из [math]X_1[/math] в [math]X_2[/math] в графе [math]D_{M_1, M_2}(J)[/math]. [math]P[/math] может и не существовать
| Лемма: |
Если в графе [math]D_{M_1, M_2}(J)[/math] нет пути из [math]X_1[/math] в [math]X_2[/math], то [math]J[/math] - искомое максимальное по мощности независимое множество в пересечении [math]M_1[/math] и [math]M_2[/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
Отметим, что если [math]X_1[/math] или [math]X_2[/math] пустые, то [math]J[/math] - база в одном из исходных матроидов [math]M_1[/math] или [math]M_2[/math] и, следовательно, искомое максимальное по мощности независимое множество в пересечении [math]M_1[/math] и [math]M_2[/math]. Таким образом, предположим, что [math]X_1[/math] и [math]X_2[/math] непусты. Пусть [math]U[/math] - множество вершин, из которых достижимы вершины из [math]X_2[/math]. Отсутствие пути из [math]X_1[/math] в [math]X_2[/math] означает, что [math]X_1 \cap U = \emptyset[/math], [math]X_2 \subseteq U[/math] и [math]\delta^- (U) = \emptyset[/math] (т.е. в [math]U[/math] не входит ни одной дуги). Тогда:
| Утверждение: |
[math]r_1 (U) \le |J \cap U|[/math] |
| [math]\triangleright[/math] | |
От противного. Пусть [math]r_1 (U) \gt |J \cap U|[/math], тогда [math]\exists z \in U \setminus (J \cap U)[/math] : [math](J \cap U) + z \in I_1[/math] при том, что [math]J + z \notin I_1[/math]. В противном случае ([math]J + z \in I_1[/math]), [math]z \in X_1[/math], то есть [math]X_1 \cap U \ne \emptyset[/math], что противоречит отсутствию пути из [math]X_1[/math] в [math]X_2[/math]. Так как [math](J \cap U) + z \in I_1[/math], а [math]J + z \notin I_1[/math],
[math]\exists y \in J \setminus U[/math] : [math]J - y + z \in I_1[/math]. Однако, тогда [math](y, z) \in A(J)[/math], что противоречит тому факту, что [math]\delta^- (U) = \emptyset[/math]. | | [math]\triangleleft[/math] |
| Утверждение: |
[math]r_2 (S \setminus U) \le |J \cap (S \setminus U)|[/math] |
| [math]\triangleright[/math] | |
От противного. Пусть [math]\exists z \in (S \setminus U) \setminus J[/math] : [math]J \cap (S \setminus U) + z \in I_2[/math]. Аналогично доказательству предыдущего утверждения, [math]\exists y \in J \setminus (S \setminus U)[/math] : [math]J - y + z \in I_2[/math]. Однако [math]J \setminus (S \setminus U) = J \cap U[/math], то есть [math](z, y)[/math] - дуга в [math]D_{M_1, M_2}(J)[/math], поэтому [math]z \in U[/math] (т.к. [math]y \in U[/math]). Противоречие. | | [math]\triangleleft[/math] |
Так как [math]|J| = |J \cap U| + |J \setminus U| \ge r_1 (U) + r_2 (S \setminus U)[/math], [math]|J| = r_1 (U) + r_2 (S \setminus U)[/math]. Таким образом, [math]J[/math] - максимальное по мощности независимое множество в пересечении [math]M_1[/math] и [math]M_2[/math]. |
| [math]\triangleleft[/math] |
| Лемма: |
[math]J' = J \bigtriangleup V(P) \in I_1 \cap I_2[/math] |
| Доказательство: |
| [math]\triangleright[/math] |
|
Пусть [math]P = z_0, y_1, z_1, ..., y_t, z_t[/math], [math]G = \{ z_1, ..., z_t \} \cup (J \setminus \{ y_1, ..., y_t \})[/math]. Тогда [math]G \subseteq S[/math], [math]|G| = |J|[/math] и дуги из [math]\{ y_1, ..., y_t \}[/math] в
[math]\{ z_1, ..., z_t \}[/math] составляют единственное полное паросочетание в [math]J \bigtriangleup G[/math]. То есть, согласно лемме о единственном паросочетании в подграфе замен, [math]G \in I_1[/math].
К тому же, [math]\forall i \ge 1 z_i \notin X_1[/math], иначе [math]P[/math] - не кратчайший путь из [math]X_1[/math] в [math]X_2[/math]. Это означает, что [math]z_i + J \notin I_1[/math], то есть
[math]r_1 (J \cup G) = r_1 (J) = r_1 (G) = |G| = |J|[/math]. Так как [math]J + z_0 \in I_1[/math], [math]G + z_0 \in I_1[/math] (т.е. [math]J' = \{ z_0, z_1, ..., z_t \} \cup (J \setminus \{ y_1, ..., y_t \}) \in I_1[/math].
Симметрично[math](G = \{ z_0, ..., z_{t - 1} \} \cup (J \setminus \{ y_1, ..., y_t \}))[/math], [math]J' \in I_2[/math] и, следовательно, [math]J' \in (I_1 \cap I_2)[/math]. |
| [math]\triangleleft[/math] |
Таким образом, получаем следующий алгоритм:
[math]J[/math] = [math]\emptyset[/math]
isMaximal = false
while (not isMaximal) {
<построить граф замен [math]D_{M_1, M_2}(J)[/math]>
[math]X_1[/math] = [math]\{ z \in S \setminus J | J + z \in I_1 \}[/math]
[math]X_2[/math] = [math]\{ z \in S \setminus J | J + z \in I_2 \}[/math]
[math]P[/math] = кратчайший путь из [math]X_1[/math] в [math]X_2[/math]
if [math](P \ne \emptyset)[/math] {
[math]J[/math] = [math]J \bigtriangleup V(P)[/math]
} else {
isMaximal = true
}
}
Источник
Chandra Chekuri — Combinatorial Optimization