Список с пропусками — различия между версиями
Kamensky (обсуждение | вклад) (связь вероятности монетки с числом уровней; различные варианты честности монетки) |
|||
| Строка 1: | Строка 1: | ||
| − | '''Список с пропусками''' (''skip | + | '''Список с пропусками''' (''skip list'') — поисковая структура данных, позволяющая производить операции поиска, добавления и удаления элемента в списке за достаточно малое время. |
| − | + | Поиск элемента в списке производится за <tex>\Theta(\log(n))</tex>; добавление и удаление элемета происходит за то же время, что и поиск, однако эти операции могут замедлить поиск в структуре. | |
| − | == | + | Такая производительность достигается за счёт добавления новых уровней. При этом нижним уровнем является исходный список, а каждый следующий уровень - список, содержащий часть элементов предыдущего уровня со ссылками на эти элементы. |
| + | |||
| + | ==Построение== | ||
Список с пропусками строится на основе существующего односвязного отсортированного списка. | Список с пропусками строится на основе существующего односвязного отсортированного списка. | ||
[[Файл:SimpleList.png]] | [[Файл:SimpleList.png]] | ||
| − | Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска | + | Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска. Соответственно, асимптотика этих операций будет составлять <tex>\Theta(\log(n))</tex>. |
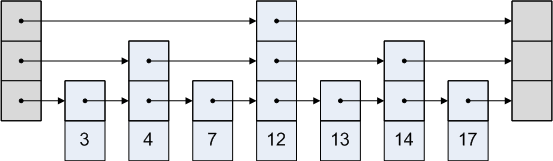
[[Файл:SkipList.png]] | [[Файл:SkipList.png]] | ||
| Строка 14: | Строка 16: | ||
==Операции над структурой== | ==Операции над структурой== | ||
===Поиск элемента=== | ===Поиск элемента=== | ||
| − | Допустим, что в нашем списке с пропусками существуют | + | Допустим, что в нашем списке с пропусками существуют <tex>k</tex> уровней, при этом первым уровнем (<tex>L_1</tex>) будет исходный список. |
В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции: | В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции: | ||
| − | # Начинаем поиск элемента в верхнем | + | # Начинаем поиск элемента в верхнем списке (<tex>L_k), рассмотрим первый элемент |
| − | + | # Переходить к следующему элементу списка, пока значение в следующей ячейке меньше или равно ключу | |
| − | # Переместиться | + | # Переместиться на один уровень вниз и перейти к пункту 2. Если рассматриваемый элемент находится на нижнем уровне - выйти из поиска |
Пример поиска числа 8 в списке из описания: | Пример поиска числа 8 в списке из описания: | ||
| Строка 25: | Строка 27: | ||
[[Файл:SkipListSearch.png]] | [[Файл:SkipListSearch.png]] | ||
| + | Рассмотрим время работы для списка с двумя уровнями. | ||
Тогда время работы алгоритма поиска будет зависеть от количества элементов на уровне <tex>L_2</tex>. Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы: | Тогда время работы алгоритма поиска будет зависеть от количества элементов на уровне <tex>L_2</tex>. Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы: | ||
| Строка 35: | Строка 38: | ||
<tex> \sqrt{n} + \dfrac{n}{\sqrt{n}} = 2 \sqrt{n}</tex> | <tex> \sqrt{n} + \dfrac{n}{\sqrt{n}} = 2 \sqrt{n}</tex> | ||
| − | + | Так же можно убедиться, что список с пропусками, имеющий <tex>k<tex> уровней, будет лучше всего работать с <tex>\sqrt[k]{n} </tex> элементами на уровне; время работы такого списка будет равно <tex>k \sqrt[k]{n} </tex>. | |
| − | + | Для <tex>\log_2{n}</tex> уровней же время работы составит <tex> \log_2{n} \times \sqrt[\log{n}]{n} = n ^ {\frac{1}{log_2{n}}} \times \log{n} = n ^ {\log_n{2}} \times \log_2{n} = 2\log_2{n}</tex> | |
| − | + | ||
| − | + | Пример поиска: | |
| − | + | <code> | |
| − | + | T* find (list <node> skip_list, K key) { // Возвращает собственно элемент | |
| − | + | node* pos = _find (skip_list, key); | |
| + | return pos->key == key ? pos : NULL; // Вернёт элемент, если он есть, иначе NULL | ||
| + | } | ||
| + | node* _find (list <node> skip_list, K key) { // Возвращает место элемента | ||
| + | node * res; | ||
| + | for (res = skip_list.begin(); res->ref != NULL; res = res->ref) { | ||
| + | while (res->key <= key) // Переходим к следующему элементу (п. 2) | ||
| + | res = res->next(); | ||
| + | } // Спускаемся на шаг вниз, если можем (п. 3) | ||
| + | return res; // Возвращаем позицию элемента, либо (в случае отсутствия) | ||
| + | } // позицию, после которой его следует вставить | ||
| + | </code> | ||
===Вставка элемента=== | ===Вставка элемента=== | ||
Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги: | Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги: | ||
| Строка 52: | Строка 66: | ||
Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется <tex>\dfrac{n}{2}</tex>, на третьем уровне <tex>\dfrac{n}{4}</tex> и т.д. На уровне <tex>\log{n}</tex> у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это <tex>\dfrac{1}{2}</tex>, на третий <tex>\dfrac{1}{4}</tex> и т.д. Вероятность попасть на уровень <tex>\log{n}</tex> равна <tex>\dfrac{1}{n}</tex>. | Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется <tex>\dfrac{n}{2}</tex>, на третьем уровне <tex>\dfrac{n}{4}</tex> и т.д. На уровне <tex>\log{n}</tex> у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это <tex>\dfrac{1}{2}</tex>, на третий <tex>\dfrac{1}{4}</tex> и т.д. Вероятность попасть на уровень <tex>\log{n}</tex> равна <tex>\dfrac{1}{n}</tex>. | ||
| − | Используя монетку с распределением отличным от {<tex>\dfrac{1}{2}</tex>, <tex>\dfrac{1}{2}</tex>}, можно влиять на количество элементов на верхних уровнях | + | Используя монетку с распределением отличным от {<tex>\dfrac{1}{2}</tex>, <tex>\dfrac{1}{2}</tex>}, можно влиять на количество элементов на верхних уровнях. Так, например, при использовании монеты с распределением {<tex>p</tex>, <tex>q</tex>}, математическое ожидание количества элементов на уровне <tex>l</tex> равно <tex>n q^l</tex>, каждый уровень будет составлять <tex>q</tex> от предыдущего; время поиска будет равно <tex>O(\dfrac{k}{q} + nq^k)</tex>. Соответственно при честной монетке и <tex>\log(n)<tex> уровней получаем оценку, полученную ранее. |
| + | Для крайних распределений: | ||
| + | * {<tex>0, 1</tex>} - <tex>O(k+n)</tex> | ||
| + | * {<tex>1, 0</tex>} - <tex>\infty</tex> (если разрешить добавление новых уровней при проталкивании элемента после броска монетки; иначе <tex>O(n)</tex>) | ||
===Удаление элемента=== | ===Удаление элемента=== | ||
| Строка 60: | Строка 77: | ||
==Псевдокод== | ==Псевдокод== | ||
| + | Наглядный, но не очень эффективный по памяти вариант списка с пропусками. | ||
| + | В узлах списка хранятся: | ||
| + | * <tex>next</tex> {{---}} следующий узел | ||
| + | * <tex>down</tex> {{---}} тот же узел на следующем уровне | ||
| + | * <tex>data</tex> {{---}} данные типа T | ||
| + | * <tex>key</tex> {{---}} ключ типа K | ||
| + | |||
| + | Конструктор | ||
<code> | <code> | ||
| − | + | skip_list (list l): | |
| − | + | list lvl = build_lvl(l); // Здесь происходит построение первого уровня | |
| − | + | while (lvl.size() > 2) | |
| − | + | lvl = build_lvl (lvl); // Добавление следующих уровней; последний содержит два элемента | |
| − | + | return t; | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | list build_lvl (list lvl) // Отсеивание нечётных элементов | ||
| + | list next_lvl; | ||
| + | node i = lvl.head(); // Перебор всех элементов lvl | ||
| + | while ((i != NULL) && (i != lvl.tail())) | ||
| + | next_lvl.push_back(node(i.key, i)); // Добавление чётного элемента; | ||
| + | i = i.next.next; // он содержит ключ и ссылку на предыдущий уровень | ||
| + | return next_lvl; | ||
| + | </code> | ||
| + | Поиск элемента по ключу: | ||
| + | <code> | ||
| + | T find (list skip_list, K key) | ||
| + | node res; | ||
| + | for (res = skip_list.head; res.ref != NULL; res = res.ref) { | ||
| + | // Cпускаемся на шаг вниз, если можем (п. 3) | ||
| + | while (res.key <= key) // Переходим к следующему элементу (п. 2) | ||
| + | res = res.next(); | ||
| + | return res.data; | ||
| + | </code> | ||
| + | Вставка: | ||
| + | <code> | ||
| + | node insert (node i, K key, T data) | ||
| + | while (i.key <= key) // Ищем подходящее место | ||
| + | i = i.next(); | ||
| + | node tmp = NULL; // Для записи в поле down | ||
| + | if i.ref != NULL // Мы не на нижнем уровне | ||
| + | tmp = insert (i.ref, key); // Рекурсивный вызов на более низком уровне | ||
| + | if tmp == NULL // Проверка броска монетки | ||
| + | return NULL; | ||
| + | i.next = new node (i.next, tmp, data, key); //Непосредственно вставка | ||
| + | if random(0,1) > 0.5 // Бросок монетки | ||
| + | return i.next; // Нужно передать новый элемент для вставки выше | ||
| + | else | ||
| + | return NULL; | ||
| + | void insert (list skip_list, K key, T data) // Обёрточка | ||
| + | insert(skip_list.head, key, data); | ||
</code> | </code> | ||
| + | Удаление: | ||
| + | <code> | ||
| + | void erase (node i, K key) | ||
| + | if (i == NULL) | ||
| + | return; | ||
| + | while (i.key <= key) // Ищем элемент | ||
| + | i = i.next(); | ||
| + | erase(i.ref, key); // Удаляем с нижних уровней | ||
| + | if (i.key == key) // Если ключ совпадает | ||
| + | delete(i); // удаляем и с этого уровня | ||
| + | void erase (list skip_list, K key) // Обёрточка | ||
| + | erase(skip_list.head, key); | ||
| + | </code> | ||
| + | ==См. также== | ||
| + | *[[Список]] | ||
| + | *[[Рандомизированное бинарное дерево поиска]] | ||
| + | *[[Поисковые структуры]] | ||
==Ссылки== | ==Ссылки== | ||
*[http://habrahabr.ru/post/111913/ Хабрахабр — Списки с пропусками] | *[http://habrahabr.ru/post/111913/ Хабрахабр — Списки с пропусками] | ||
Версия 18:29, 7 июня 2015
Список с пропусками (skip list) — поисковая структура данных, позволяющая производить операции поиска, добавления и удаления элемента в списке за достаточно малое время.
Поиск элемента в списке производится за ; добавление и удаление элемета происходит за то же время, что и поиск, однако эти операции могут замедлить поиск в структуре.
Такая производительность достигается за счёт добавления новых уровней. При этом нижним уровнем является исходный список, а каждый следующий уровень - список, содержащий часть элементов предыдущего уровня со ссылками на эти элементы.
Содержание
Построение
Список с пропусками строится на основе существующего односвязного отсортированного списка.
Добавив дополнительные уровни, каждый из которых представляет предыдущий уровень без нечетных элементов, мы получим возможность осуществлять поиск, вставку и удаление элементов подобно операциям с двоичным деревом поиска. Соответственно, асимптотика этих операций будет составлять .
Операции над структурой
Поиск элемента
Допустим, что в нашем списке с пропусками существуют уровней, при этом первым уровнем () будет исходный список.
В таком случае алгоритм поиска в этой структуре будет представлять из себя следующие операции:
- Начинаем поиск элемента в верхнем списке (. Представим, что на этот уровень у нас случайным образом попало несколько элементов. Следовательно в худшем случае поиска мы получим следующую оценку на время работы:
Минимизируя, мы получаем, что
В итоге время за которое мы найдем элемент в списке с пропусками с двумя уровнями будет равняться:
Так же можно убедиться, что список с пропусками, имеющий элементами на уровне; время работы такого списка будет равно . Для уровней же время работы составит
Пример поиска:
T* find (list <node> skip_list, K key) { // Возвращает собственно элемент
node* pos = _find (skip_list, key);
return pos->key == key ? pos : NULL; // Вернёт элемент, если он есть, иначе NULL
}
node* _find (list <node> skip_list, K key) { // Возвращает место элемента
node * res;
for (res = skip_list.begin(); res->ref != NULL; res = res->ref) {
while (res->key <= key) // Переходим к следующему элементу (п. 2)
res = res->next();
} // Спускаемся на шаг вниз, если можем (п. 3)
return res; // Возвращаем позицию элемента, либо (в случае отсутствия)
} // позицию, после которой его следует вставить
Вставка элемента
Для вставки элемента в список с пропусками, нам необходимо выполнить следующие шаги:
- Найти с помощью алгоритма поиска позицию, куда нам надо вставить этот элемент
- Вставить наш элемент в нижний уровень списка с пропусками
- «Подбросить монетку» и в зависимости от результата протолкнуть элемент на уровень выше
- Повторять предыдущий шаг до тех пор, пока у нас «подброс монетки» дает положительный результат
Таким образом, если использовать честную монету, то математическое ожидание количества элементов на втором уровне равняется , на третьем уровне и т.д. На уровне у нас окажется один элемент. Ну и соответственно вероятности попасть элементу на второй уровень — это , на третий и т.д. Вероятность попасть на уровень равна .
Используя монетку с распределением отличным от {, }, можно влиять на количество элементов на верхних уровнях. Так, например, при использовании монеты с распределением {, }, математическое ожидание количества элементов на уровне равно , каждый уровень будет составлять от предыдущего; время поиска будет равно . Соответственно при честной монетке и } -
- {} - (если разрешить добавление новых уровней при проталкивании элемента после броска монетки; иначе )
Удаление элемента
Алгоритм удаления достаточно тривиален.
- Найти удаляемый элемент
- Удалить его со всех уровней
Псевдокод
Наглядный, но не очень эффективный по памяти вариант списка с пропусками.
В узлах списка хранятся:
- — следующий узел
- — тот же узел на следующем уровне
- — данные типа T
- — ключ типа K
Конструктор
skip_list (list l):
list lvl = build_lvl(l); // Здесь происходит построение первого уровня
while (lvl.size() > 2)
lvl = build_lvl (lvl); // Добавление следующих уровней; последний содержит два элемента
return t;
list build_lvl (list lvl) // Отсеивание нечётных элементов
list next_lvl;
node i = lvl.head(); // Перебор всех элементов lvl
while ((i != NULL) && (i != lvl.tail()))
next_lvl.push_back(node(i.key, i)); // Добавление чётного элемента;
i = i.next.next; // он содержит ключ и ссылку на предыдущий уровень
return next_lvl;
Поиск элемента по ключу:
T find (list skip_list, K key)
node res;
for (res = skip_list.head; res.ref != NULL; res = res.ref) {
// Cпускаемся на шаг вниз, если можем (п. 3)
while (res.key <= key) // Переходим к следующему элементу (п. 2)
res = res.next();
return res.data;
Вставка:
node insert (node i, K key, T data)
while (i.key <= key) // Ищем подходящее место
i = i.next();
node tmp = NULL; // Для записи в поле down
if i.ref != NULL // Мы не на нижнем уровне
tmp = insert (i.ref, key); // Рекурсивный вызов на более низком уровне
if tmp == NULL // Проверка броска монетки
return NULL;
i.next = new node (i.next, tmp, data, key); //Непосредственно вставка
if random(0,1) > 0.5 // Бросок монетки
return i.next; // Нужно передать новый элемент для вставки выше
else
return NULL;
void insert (list skip_list, K key, T data) // Обёрточка
insert(skip_list.head, key, data);
Удаление:
void erase (node i, K key)
if (i == NULL)
return;
while (i.key <= key) // Ищем элемент
i = i.next();
erase(i.ref, key); // Удаляем с нижних уровней
if (i.key == key) // Если ключ совпадает
delete(i); // удаляем и с этого уровня
void erase (list skip_list, K key) // Обёрточка
erase(skip_list.head, key);