|
|
| Строка 248: |
Строка 248: |
| | |style="background-color:#FFF;padding:2px 20px"| <tex>r(4)</tex> | | |style="background-color:#FFF;padding:2px 20px"| <tex>r(4)</tex> |
| | |} | | |} |
| − |
| |
| − | == Формальное описание ==
| |
| − | === Базовые операции ===
| |
| − | Теперь опишем алгоритм формально.
| |
| − |
| |
| − | Для построения множества состояний определим базовые операции <tex>closure (I)</tex> и <tex>goto (I, X)</tex>, где <tex>I</tex> – множество ситуаций, <tex>X</tex> – символ грамматики (терминал или нетерминал). Операция <tex>closure</tex> добавляет ситуации к множеству ситуаций, у которых точка стоит слева от нетерминала. Добавляются те ситуации, которые получаются из правил, в левой части которого находится этот нетерминал.
| |
| − |
| |
| − | {| border="0"
| |
| − | |align="left" colspan="4"|
| |
| − | <font size=2>
| |
| − | [] '''closure''' (I)
| |
| − | '''do'''
| |
| − | '''for''' каждой ситуации [A <tex>\to</tex> w.Xv] из I
| |
| − | '''for''' каждого правила грамматики X <tex>\to</tex> u
| |
| − | I += [X <tex>\to</tex> .u] <font color=green> // Операция += добавляет элемент к множеству </font>
| |
| − | '''while''' I изменилось
| |
| − | '''return''' I
| |
| − | </font>
| |
| − | |}
| |
| − |
| |
| − |
| |
| − | Операция <tex>goto</tex> "переносит" точку после символа <tex>X</tex>. Это означает переход из одного состояния в другое под воздействием символа <tex>X</tex>.
| |
| − |
| |
| − | {| border="0"
| |
| − | |align="left" colspan="4"|
| |
| − | <font size=2>
| |
| − | [] '''goto''' (I, X)
| |
| − | J={} <font color=green> // {} обозначает пустое множество </font>
| |
| − | '''for''' каждой ситуации [A <tex>\to</tex> w.Xv] из I
| |
| − | J += [A <tex> \to </tex>wX.v]
| |
| − | '''return''' closure (J)
| |
| − | </font>
| |
| − | |}
| |
| − |
| |
| − | === Алгоритм построения конечного автомата ===
| |
| − | Теперь обсудим алгоритм построения анализатора. Обозначим <tex>T</tex> множество состояний, <tex>E</tex> – множество переходов.
| |
| − |
| |
| − | {| border="0"
| |
| − | |align="left" colspan="4"|
| |
| − | <font size=2>
| |
| − | E, T '''build'''()
| |
| − | E = {}
| |
| − | T = {closure ([S' <tex>\to</tex> .S])}
| |
| − | '''do'''
| |
| − | '''for''' каждого состояния I из T
| |
| − | '''for''' каждой ситуации [A <tex>\to</tex> w.Xv] из I
| |
| − | J = goto(I, X)
| |
| − | T += {J} <font color=green> // ко множеству состояний добавляется новое состояние </font>
| |
| − | E += (I <tex>\to</tex> J) <font color=green> // ко множеству ребер добавляется ребро, идущее из состояния I в состояние J. Этот переход осуществляется по символу X </font>
| |
| − | '''while''' E или T изменились
| |
| − | '''return''' E, T
| |
| − | </font>
| |
| − | |}
| |
| − |
| |
| − | Поскольку для символа <tex>\$</tex> операция <tex>goto(I , \$)</tex> не определена , мы выполняем действие <tex>accept</tex>.
| |
| | | | |
| | == Пример LR(0)-разбора == | | == Пример LR(0)-разбора == |
LR(0)-разборщик это частный случай LR(k)-разборщикa, заметим, что в данном случае [math]k=0[/math], то есть решение о своих действиях принимается только на основании содержимого стека, не учитывая символы входной цепочки.
Построение автомата и управляющей таблицы
Как было сказано в статье про LR(k)-разборщик, управляющая программа одинакова для всех LR-анализаторов, а таблица и автомат изменяются от одного анализатора к другому.
Автомат
Каждое состояние автомата будет состоять из LR(0)-ситуации.
| Определение: |
| Пусть [math]\Gamma =\langle \Sigma, N, S, P \rangle[/math] — КС-грамматика и [math]A \to w_1 w_2 \in P[/math]. Композицию [math][A \to w_1 \cdot w_2] [/math] назовем LR(0)-ситуацией (англ. LR(0)-item) |
В начале работы стек пуст, и указатель входной цепочки находится перед ее первым символом. Этому состоянию соответствует ситуация [math][E_0 \to \cdot E][/math], где [math]E_0[/math] — нетерминал, добавленный при пополнении грамматики, [math]E[/math] — стартовый нетерминал. Наховем это состояние [math]0[/math]. Входная цепочка может начинаться с любого терминального символа, с которого начинается правая часть любого правила с левой частью [math]E[/math]. Построим соответствующий переход:
[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\varepsilon} {[} B \to \cdot \gamma] [/math]
Теперь мы должны выяснить, что произойдет, если анализатор выполнит перенос. Предположим, что мы выполним перенос [math]c[/math] или перенос [math]B[/math]:
[math]{[} A \to \alpha \cdot c \beta] \xrightarrow{\text{c}} {[} A \to \alpha c \cdot \beta] [/math]
[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\text{B}} {[} A \to \alpha B \cdot \beta] [/math]
Таким образом, мы определяем новые состояния, в которое автомат перейдет после переноса того или иного терминала или нетерминала.
Заметим, что хранить в каждом состоянии только по одной ситуации не имеет смысла, поэтому пусть в каждое стостояние будет представлять множество ситуаций. Для этого определим базовые операции [math]closure (I)[/math] и [math]goto (I, X)[/math], где [math]I[/math] – множество ситуаций, [math]X[/math] – символ грамматики (терминал или нетерминал). Операция [math]closure[/math] добавляет ситуации к множеству ситуаций, у которых точка стоит слева от нетерминала. Добавляются те ситуации, которые получаются из правил, в левой части которого находится этот нетерминал.
|
[] closure (I)
do
for каждой ситуации [A [math]\to[/math] w.Xv] из I
for каждого правила грамматики X [math]\to[/math] u
I += [X [math]\to[/math] .u] // Операция += добавляет элемент к множеству
while I изменилось
return I
|
Операция [math]goto[/math] "переносит" точку после символа [math]X[/math]. Это означает переход из одного состояния в другое под воздействием символа [math]X[/math].
|
[] goto (I, X)
J={} // {} обозначает пустое множество
for каждой ситуации [A [math]\to[/math] w.Xv] из I
J += [A [math] \to [/math]wX.v]
return closure (J)
|
Теперь обсудим алгоритм построения конечного автомата. Обозначим [math]T[/math] множество состояний, [math]E[/math] – множество переходов.
|
E, T build()
E = {}
T = {closure ([S' [math]\to[/math] .S])}
do
for каждого состояния I из T
for каждой ситуации [A [math]\to[/math] w.Xv] из I
J = goto(I, X)
T += {J} // ко множеству состояний добавляется новое состояние
E += (I [math]\to[/math] J) // ко множеству ребер добавляется ребро, идущее из состояния I в состояние J. Этот переход осуществляется по символу X
while E или T изменились
return E, T
|
Поскольку для символа [math]\$[/math] операция [math]goto(I , \$)[/math] не определена , мы выполняем действие [math]accept[/math].
В итоге получился автомат.
Построение управляющей таблицы
После того, как автомат построен, перейдем к построению управляющей таблицы.
Обращение к таблице происходит слудующим образом [math]\mathtt{T[state, token]}[/math], где
- [math]\mathtt{state}[/math] — состояние автомата,
- [math]\mathtt{token}[/math] — входной символ;
В таблице информация имеет следующий вид:
struct Cell
enum:
Shift
Reduce
Accept // допуск
Error // ошибка
struct Shift
state: int // переход в стостояние state
struct Reduce
rule: int // свертка по правилу rule
Иллюстрация алгоритма
Для иллюстрации алгоритма LR(0)-разборщика мы будем использовать грамматику:
[math]
E \to E + T \\
E \to T \\
T \to {\bf n} \\
T \to (E) \\
[/math]
Пополнение грамматики
Для начала переходим к Пополненной грамматике:
[math]
E_0 \to E \\
E \to E + T \\
E \to T \\
T \to {\bf n} \\
T \to (E) \\
[/math]
Построение автомата
В начале работы стек пуст, и указатель входной цепочки находится перед ее первым символом. Этому состоянию соответствует ситуация [math][E_0 \to \cdot E][/math].
Для терминалов или нетерминалой, мы строим переходы к другим ситуациям по следующей схеме:
[math]{[} A \to \alpha \cdot c \beta] \xrightarrow{\text{c}} {[} A \to \alpha c \cdot \beta] [/math]
[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\text{B}} {[} A \to \alpha B \cdot \beta] [/math]
[math]{[} A \to \alpha \cdot B \beta] \xrightarrow{\varepsilon} {[} B \to \cdot \gamma] [/math]
Получаем следующий НКА:
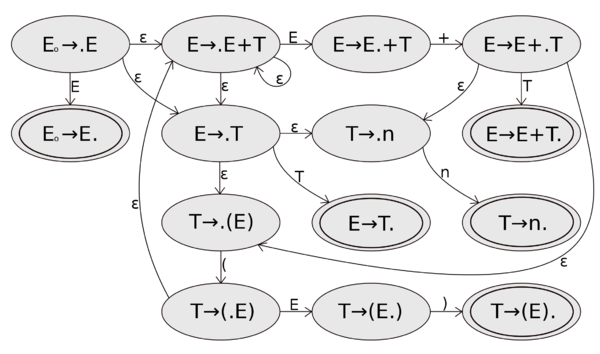
Избавимся от [math]\varepsilon[/math]-переходов и получим ДКА:
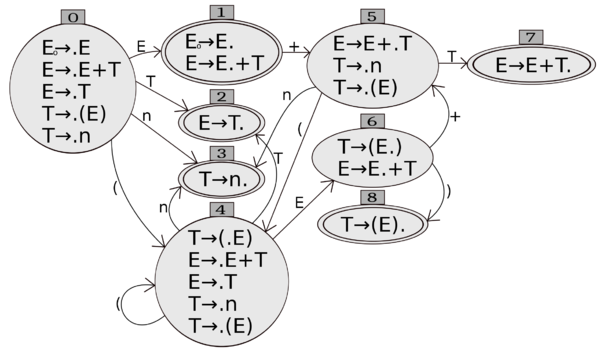
Управляющая таблица
Теперь можно построить управляющую таблицу.
Поступим следующим образом:
1. для каждого ребра [math]I \xrightarrow{\text{X}} J [/math] мы поместим в позицию [math][I,X][/math] таблицы
- [math]s\ J[/math] (сокр. от shift) , если [math]X[/math] — терминал,
- [math]J[/math], если [math]X[/math] — нетерминал.
2. для состояния, содержащего ситуацию [math][A\to w \cdot][/math], поместим [math]r(n)[/math] (сокр. от reduce) в позицию [math][I, Y][/math] для каждого терминала [math]Y[/math], где [math]n[/math] — это номер правила в изначальной грамматике.
3. пустая ячейка означает ошибочную ситуацию.
Вспомним грамматику и пронумеруем правила для 2 пункта:
[math]
(0)\ E_0 \to E\\
(1)\ E \to E + T\\
(2)\ E \to T\\
(3)\ T \to {\bf n} \\
(4)\ T \to (E) \\
[/math]
Управляющая таблица будет выглядеть так:
|
|
[math]E[/math]
|
[math]T[/math]
|
[math]n[/math]
|
[math]+[/math]
|
[math]([/math]
|
[math])[/math]
|
[math]\$[/math]
|
| [math]0[/math]
|
[math]1[/math]
|
[math]2[/math]
|
[math]s3[/math]
|
|
[math]s4[/math]
|
|
|
| [math]1[/math]
|
|
|
|
[math]s5[/math]
|
|
|
[math]r(0)[/math]
|
| [math]2[/math]
|
|
|
|
[math]r(2)[/math]
|
|
[math]r(2)[/math]
|
[math]r(2)[/math]
|
| [math]3[/math]
|
|
|
|
[math]r(3)[/math]
|
|
[math]r(3)[/math]
|
[math]r(3)[/math]
|
| [math]4[/math]
|
[math]6[/math]
|
[math]2[/math]
|
[math]s3[/math]
|
|
[math]s4[/math]
|
|
|
| [math]5[/math]
|
|
[math]7[/math]
|
[math]s3[/math]
|
|
[math]s4[/math]
|
|
|
| [math]6[/math]
|
|
|
|
[math]s5[/math]
|
|
[math]s8[/math]
|
|
| [math]7[/math]
|
|
|
|
[math]r(1)[/math]
|
|
[math]r(1)[/math]
|
[math]r(1)[/math]
|
| [math]8[/math]
|
|
|
|
[math]r(4)[/math]
|
|
[math]r(4)[/math]
|
[math]r(4)[/math]
|
Пример LR(0)-разбора
Пример будет для строки [math](n_1+n_2)+n_3[/math]
| Строка
|
Стек
|
[math]s = top()[/math]
|
[math]a = w[ip][/math]
|
[math]action[s,a][/math]
|
Комментарий
|
| [math](n_1+n_2)+n_3\$[/math]
|
[math]0[/math]
|
[math]0[/math]
|
[math]([/math]
|
[math]shift\ 4[/math]
|
Перенос [math]"("[/math]
|
| [math]n_1+n_2)+n_3\$[/math]
|
[math]0\ (4[/math]
|
[math]4[/math]
|
[math]n_1[/math]
|
[math]shift\ 3[/math]
|
Перенос [math]"n_1"[/math]
|
| [math]+n_2)+n_3\$[/math]
|
[math]0\ (4\ n_{1}3[/math]
|
[math]3[/math]
|
[math]+[/math]
|
[math]reduce\ 3[/math]
|
Свертка: [math]T \to \bf n[/math]
|
| [math]+n_2)+n_3\$[/math]
|
[math]0\ (4\ T2[/math]
|
[math]2[/math]
|
[math]+[/math]
|
[math]reduce\ 2[/math]
|
Свертка: [math]E \to T[/math]
|
| [math]+n_2)+n_3\$[/math]
|
[math]0\ (4\ E6[/math]
|
[math]6[/math]
|
[math]+[/math]
|
[math]shift\ 5[/math]
|
Перенос [math]"+"[/math]
|
| [math]n_2)+n_3\$[/math]
|
[math]0\ (4\ E6\ +5[/math]
|
[math]5[/math]
|
[math]n_2[/math]
|
[math]shift\ 3[/math]
|
Перенос [math]"n_2"[/math]
|
| [math])+n_3\$[/math]
|
[math]0\ (4\ E6\ +5\ n_23[/math]
|
[math]3[/math]
|
[math])[/math]
|
[math]reduce\ 3 [/math]
|
Свертка: [math]T \to \bf n[/math]
|
| [math])+n_3\$[/math]
|
[math]0\ (4\ E6\ +5\ T7[/math]
|
[math]7[/math]
|
[math])[/math]
|
[math]reduce\ 1 [/math]
|
Свертка: [math]E \to E + T[/math]
|
| [math])+n_3\$[/math]
|
[math]0\ (4\ E6[/math]
|
[math]6 [/math]
|
[math])[/math]
|
[math]shift\ 8[/math]
|
Перенос [math]")"[/math]
|
| [math]+n_3\$[/math]
|
[math]0\ (4\ E6\ )8[/math]
|
[math]8 [/math]
|
[math]+[/math]
|
[math]reduce\ 4[/math]
|
Свертка: [math]T \to (E)[/math]
|
| [math]+n_3\$[/math]
|
[math]0\ T2[/math]
|
[math]2[/math]
|
[math]+[/math]
|
[math]reduce\ 2[/math]
|
Свертка: [math]E \to T[/math]
|
| [math]+n_3\$[/math]
|
[math]0\ E1[/math]
|
[math]1[/math]
|
[math]+[/math]
|
[math]shift\ 5[/math]
|
Перенос [math]"+"[/math]
|
| [math]n_3\$[/math]
|
[math]0\ E1\ +5[/math]
|
[math]5[/math]
|
[math]n_3[/math]
|
[math]shift\ 3[/math]
|
Перенос [math]"n_3"[/math]
|
| [math]\$[/math]
|
[math]0\ E1\ +5\ n_33[/math]
|
[math]3[/math]
|
[math]\$[/math]
|
[math]reduce\ 3[/math]
|
Свертка: [math]T \to \bf n[/math]
|
| [math]\$[/math]
|
[math]0\ E1\ +5\ T7[/math]
|
[math]7[/math]
|
[math]\$[/math]
|
[math]reduce\ 1[/math]
|
Свертка: [math]E \to E + T[/math]
|
| [math]\$[/math]
|
[math]0\ E1[/math]
|
[math]1[/math]
|
[math]\$[/math]
|
[math]reduce\ 0[/math]
|
Допуск
|
См. также
Источники информации
- Альфред Ахо, Рави Сети, Джеффри Ульман. Компиляторы. Принципы, технологии, инструменты. Издательство Вильямс, 2003. Стр. 301 - 326.
- Терехов Ан.А., Вояковская Н., Булычев Д., Москаль А. - Разработка компиляторов на платформе .NET - Восходящие анализаторы
- Б.К.Мартыненко. Языки и трансляции. Стр. 198 - 223
- Лекции по теории формальных языков, LR(0)-, SLR(1)-, LR(1)- и LALR(1)-анализ

