Алгоритм Борувки — различия между версиями
Novik (обсуждение | вклад) м |
Novik (обсуждение | вклад) (→Пример) |
||
| Строка 63: | Строка 63: | ||
! Изображение !! Компоненты связности !! Описание | ! Изображение !! Компоненты связности !! Описание | ||
|- | |- | ||
| − | |[[Файл: | + | |[[Файл:Boruvka_1.png|250px]] |
| − | | | + | | {A}<br/>{B}<br/>{C}<br/>{D}<br/>{E}<br/>{F}<br/>{G} |
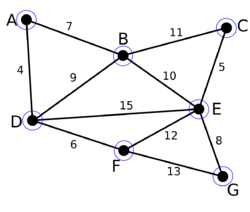
| − | |Начальный граф <tex> | + | |Начальный граф <tex>G</tex>. Каждая вершина является компонентой (синие окружности). |
|- | |- | ||
| − | |[[Файл: | + | |[[Файл:Boruvka_2.png|250px]] |
| − | | < | + | | {ABDF}<br/>{CEG} |
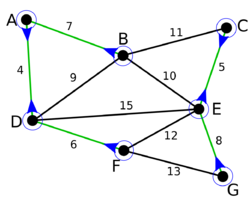
| − | + | |На первой итерации внешнего цикла для каждой компоненты были добавлены минимальные сопряженные ребра. Некоторые ребра добавлены несколько раз (<tex dpi = 120>AD</tex> и <tex dpi = 120>CE</tex>). Осталось две компоненты. | |
|- | |- | ||
| − | |[[Файл: | + | |[[Файл:Boruvka_3.png|250px]] |
| − | | < | + | | {ABCDEFG} |
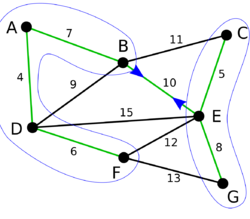
| − | + | |На последней итерации внешнего цикла было добавлено минимальное ребро, соединяющее две оставшиеся компоненты (ребро <tex dpi = 120>BE</tex>). Осталась одна компонента. Минимальное остовное дерево графа <tex dpi = 120>G</tex> построено. | |
|- | |- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
Версия 21:38, 26 сентября 2015
Алгоритм Борувки (англ. Borůvka's algorithm) — алгоритм поиска минимального остовного дерева (англ. minimum spanning tree, MST) во взвешенном неориентированном связном графе. Впервые был опубликован в 1926 году Отакаром Борувкой.
Содержание
Описание алгоритма
- Построим граф . Изначально содержит все вершины из и не содержит ребер (каждая вершина в графе — отдельная компонента связности).
- Будем добавлять в ребра следующим образом, пока не является деревом
- Для каждой компоненты связности находим минимальное по весу ребро, которое связывает эту компоненту с другой.
- Добавим в все найденные рёбра.
- Получившийся граф является минимальным остовным деревом графа .
Данный алгоритм может работать неправильно, если в графе есть ребра равные по весу. Например, полный граф из трех вершин, вес каждого ребра равен один. В могут быть добавлены все три ребра. Избежать эту проблему можно, выбирая в первом пункте среди ребер, равных по весу, ребро с наименьшим номером.
Доказательство будем проводить, считая веса всех ребер различными.
Доказательство корректности
| Лемма: |
Рассмотрим связный неориентированный взвешенный граф с инъективной весовой функцией .
Тогда после первой итерации главного цикла алгоритма Борувки получившийся подграф можно достроить до MST. |
| Доказательство: |
| Предположим обратное: пусть любое MST графа не содержит . Рассмотрим какое-нибудь MST. Тогда существует ребро из такое что не принадлежит MST. Добавив ребро в MST, получаем цикл в котором не максимально, т.к оно было минимальным. Тогда, исходя из критерия Тарьяна, получаем противоречие. |
| Теорема: |
Алгоритм Борувки строит MST. |
| Доказательство: |
|
Очевидно, что алгоритм Борувки строит дерево.Будем доказывать что после каждой итерации главного цикла в алгоритме Борувки текущий подграф можно достроить до MST. Докажем это по индукции. База. (см. Лемму). Переход. Пусть лес , получившийся после итераций алгоритма, можно достроить до MST. Докажем, что после итерации получившийся лес можно достроить до MST. Предположим обратное: нельзя достроить до MST. Тогда существует = MST графа , содержащее и не содержащее . Тогда рассмотрим цикл, получающийся добавлением в какого-нибудь ребра из . На этом цикле имеется ребро, большее по весу чем ребро , иначе компонента для которой является минимальным ребром ни с кем больше ни связана. Исходя из критерия Тарьяна, получаем противоречие. Получаем. можно достроить до MST. Следовательно предположение индукции верно. |
Реализация
У вершины есть поле comp — компонента связности, которой принадлежит эта вершина.
// — исходный граф // — весовая функция function while for Component // Component — множество компонент связности в // для каждой компоненты связности вес минимального ребра = // разбиваем граф на компоненты связности обычным dfs-ом for if if if for Component // добавляем ребро если его не было в return |
Пример
Асимптотика
Внешний цикл повторяется раз, так как количество компонент связности каждый раз уменьшается в двое и изначально равно количеству вершин. Что же касается внутреннего цикла, то он выполняется за , где — количество рёбер в исходном графе. Следовательно конечное время работы алгоритма .