Построение компонент вершинной двусвязности — различия между версиями
м |
Novik (обсуждение | вклад) (→Двупроходный алгоритм) |
||
| Строка 7: | Строка 7: | ||
'''Второй проход | '''Второй проход | ||
[[Точка сочленения, эквивалентные определения|Точка сочленения]] принадлежит как минимум двум компонентам вершинной двусвязности. | [[Точка сочленения, эквивалентные определения|Точка сочленения]] принадлежит как минимум двум компонентам вершинной двусвязности. | ||
| − | Вершина <tex> v \ne root </tex> является точкой сочленения, если у нее есть сын <tex> u : return[u] \ | + | Вершина <tex> v \ne root </tex> является точкой сочленения, если у нее есть сын <tex> u : return[u] \geqslant enter[v] </tex>. <br> Это также значит, что ребро <tex> vu </tex> содержится в другой компоненте вершинной двусвязности, нежели ребро по которому мы пришли в вершину <tex> v </tex> , используя поиск в глубину. <br> |
Используем это свойство, чтобы окрасить компоненты вершинной двусвязности в различные цвета.<br> | Используем это свойство, чтобы окрасить компоненты вершинной двусвязности в различные цвета.<br> | ||
| − | + | === Псевдокод второго прохода === | |
{| width = 100% | {| width = 100% | ||
|- | |- | ||
| | | | ||
| − | dfs(<tex>v | + | <tex>dfs</tex>(<tex>v</tex>, color, parent): |
| − | + | '''for''' <tex> u \in V : (v, u) \in E</tex>: | |
| − | + | '''if''' <tex>u</tex> == parent | |
| − | + | continue | |
| − | + | '''if''' '''not''' visited[<tex>u</tex>] | |
| − | + | '''if''' return[<tex>u</tex>] <tex>\geqslant</tex> enter[<tex>v</tex>] | |
| − | <tex> | + | newColor <tex>\leftarrow</tex> maxColor++ |
| − | <tex> | + | col[<tex>vu</tex>] <tex>\leftarrow</tex> newColor |
| − | dfs(<tex>u, | + | <tex>dfs</tex>(<tex>u</tex>, newColor, <tex>v</tex>) |
| − | + | '''else''' | |
| − | <tex> | + | col[<tex>vu</tex>] <tex>\leftarrow</tex> color |
| − | dfs(<tex>u, | + | <tex>dfs</tex>(<tex>u</tex>, color, <tex>v</tex>) |
| − | + | '''else''' | |
| − | + | '''if''' enter[<tex>u</tex>] <tex>\leqslant</tex> enter[<tex>v</tex>] | |
| − | <tex> | + | col[<tex>vu</tex>] <tex>\leftarrow</tex> color |
| − | + | ... | |
| − | + | '''for''' <tex> v \in V</tex>: | |
| − | + | '''if''' '''not''' visited[<tex>v</tex>] | |
| − | + | <tex>dfs</tex>(<tex>v</tex>, -1, -1) | |
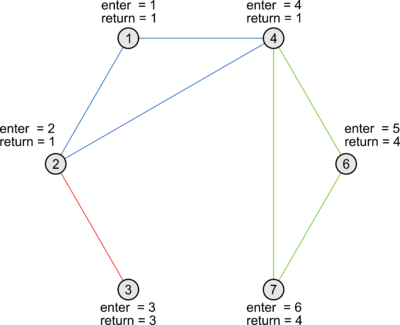
|width = "310px" |[[Файл:Vertex_doubleconnection_1.png|thumb|center|400px|Компоненты обозначены разным цветом]] | |width = "310px" |[[Файл:Vertex_doubleconnection_1.png|thumb|center|400px|Компоненты обозначены разным цветом]] | ||
|} | |} | ||
Версия 20:36, 9 ноября 2015
Содержание
Двупроходный алгоритм
Найти компоненты вершинной двусвязности неориентированного графа можно с помощью обхода в глубину.
Первый проход
Используем первый проход, чтобы найти точки сочленения.
Второй проход
Точка сочленения принадлежит как минимум двум компонентам вершинной двусвязности.
Вершина является точкой сочленения, если у нее есть сын .
Это также значит, что ребро содержится в другой компоненте вершинной двусвязности, нежели ребро по которому мы пришли в вершину , используя поиск в глубину.
Используем это свойство, чтобы окрасить компоненты вершинной двусвязности в различные цвета.
Псевдокод второго прохода
(, color, parent): for : if == parent continue if not visited[] if return[] enter[] newColor maxColor++ col[] newColor (, newColor, ) else col[] color (, color, ) else if enter[] enter[] col[] color ... for : if not visited[] (, -1, -1) |
Ребра каждой из компонент вершинной двусвязности окажутся окрашенными в свой цвет.
В алгоритме выполняется два прохода , каждый из которых работает . Значит время работы алгоритма .
Однопроходный алгоритм
Заведем стек, в который будем записывать все дуги в порядке их обработки. Если обнаружена точка сочленения, дуги очередного блока окажутся в этом стеке, начиная с дуги дерева обхода, которая привела в этот блок, до верхушки стека.
Таким образом, каждый раз находя компоненту вершинной двусвязности мы сможем покрасить все ребра, содержащиеся в ней, в новый цвет.
Доказательство корректности алгоритма
Предположим, что граф содержит точку сочленения , за которой следует один или несколько блоков. Вершины из этих блоков образуют подмножество . В таком случае:
- Все вершины являются потомками в дереве обхода;
- Все вершины будут пройдены в течение периода серого состояния ;
- В не может быть обратных дуг из в .
Значит все дуги будут будут добавлены в стек после дуги ведущей из точки сочленения в блок. В стеке в момент обнаружения точки сочленения будут находиться только дуги блока, связанного с ней, т.к. блоки найденные до него (если таковые имеются) будет уже извлечены из стека и покрашены в свой цвет.
Псевдокод:
dfs() ++ для всех вершин смежных : если ( родитель) переходим к следующей итерации если ( не посещена) добавить в стек ребро dfs() если () новый цвет пока (ребро не равно вершине стека) [вершина стека] извлечь вершину стека извлечь вершину стека если () иначе если () добавить в стек ребро если () start() для всех вершин графа: если ( не посещена) dfs(, -1)
Во время алгоритма совершается один проход , который работает за . Внутри него совершается еще цикл, который суммарно выполняет операций, т.к. каждое ребро может быть добавлено в стек только один раз. Следовательно, общее время работы алгоритма
Литература
- В.А.Кузнецов, А.М.Караваев. "Оптимизация на графах" - Петрозаводск, Издательство ПетрГУ 2007