Целочисленный двоичный поиск

Целочисленный двоичный поиск (бинарный поиск) (англ. binary search) — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.

Схема бинарного поиска

Формулировка задачи

Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Требуется найти позицию, на которой находится заданный элемент. Для этой задачи мы и можем использовать двоичный поиск.

Принцип работы

Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект. Или же, в зависимости от постановки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие — это левосторонний/правосторонний двоичный поиск.

Правосторонний/левосторонний целочисленный двоичный поиск

Для простоты дальнейших определений будем считать, что [math]a[0] = -\infty[/math] и что [math]a[n+1] = +\infty[/math] (массив нумеруется с [math]1[/math]).

Определение:

Правосторонний бинарный поиск (англ. rightside binary search) — бинарный поиск, с помощью которого мы ищем [math] \max\limits_{i \in [0,n]} \{i \mid a[i] \leqslant x\} [/math], где [math]a[/math] — массив, а [math]x[/math] — искомый ключ

Определение:

Левосторонний бинарный поиск (англ. leftside binary search) — бинарный поиск, с помощью которого мы ищем [math] \min\limits_{i \in [0,n]}\{i \mid a[i] \geqslant x\} [/math], где [math]a[/math] — массив, а [math]x[/math] — искомый ключ

Использовав эти два вида двоичного поиска, мы можем найти отрезок позиций [math][l,r][/math] таких, что [math]\forall i \in [l,r] : a[i] = x[/math] и [math] \forall i \notin [l,r] : a[i] \neq x [/math]

Пример:

Задан отсортированный массив [math][1, 2, 2, 2, 2, 3, 5, 8, 9, 11], x = 2[/math].

Правосторонний поиск двойки выдаст в результате [math]5[/math], в то время как левосторонний выдаст [math]2[/math] (нумерация с единицы).

От сюда следует, что количество подряд идущих двоек равно длине отрезка [math][2;5][/math], то есть [math]4[/math].

Если искомого элемента в массиве нет, то правосторонний поиск выдаст минимальный элемент, больший искомого, а левосторонний наоборот, максимальный элемент, меньший искомого.

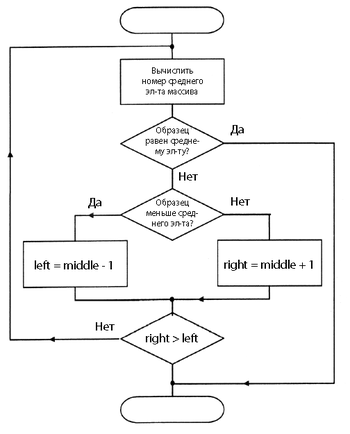
Алгоритм двоичного поиска

Идея поиска заключается в том, чтобы брать элемент посередине, между границами, и сравнивать его с искомым. Если искомое больше(в случае правостороннего — не меньше), чем элемент сравнения, то сужаем область поиска так, чтобы новая левая граница была равна индексу середины предыдущей области. В противном случае присваиваем это значение правой границе. Проделываем эту процедуру до тех пор, пока правая граница больше левой более чем на [math]1[/math]. В случае правостороннего бинарного поиска ответом будет индекс [math]l[/math], а в случае левостороннего — [math]r[/math].

Код

int binSearch(int[] a, int key):   // Запускаем бинарный поиск
    int l = 0                      // l, r — левая и правая границы
    int r = len(a) + 1    
    while l < r - 1                // Запускаем цикл
        m = (l + r) / 2            // m — середина области поиска
        if a[m] < key
            l = m
        else 
            r = m                  // Сужение границ
    return r

В случае правостороннего поиска изменится знак сравнения при сужении границ на [math]a[m] \leqslant k[/math].

Инвариант цикла: пусть левый индекс не больше искомого элемента, а правый — строго больше, тогда если [math]l = r - 1[/math], то понятно, что [math]l[/math] — самое правое вхождение (так как следующее уже больше).

Несколько слов об эвристиках

Эвристика с завершением поиска, при досрочном нахождении искомого элемента

Заметим, что если нам необходимо просто проверить наличие элемента в упорядоченном множестве, то можно использовать любой из правостороннего и левостороннего поиска. При этом будем на каждой итерации проверять "не попали ли мы в элемент, равный искомому", и в случае попадания заканчивать поиск.

Эвристика с запоминанием ответа на предыдущий запрос

Пусть дан отсортированный массив чисел, упорядоченных по неубыванию. Также пусть запросы приходят в таком порядке, что каждый следующий не меньше, чем предыдущий. Для ответа на запрос будем использовать левосторонний двоичный поиск. При этом после того как обработался первый запрос, запомним чему равно [math]l[/math], запишем его в переменную [math]startL[/math]. Когда будем обрабатывать следующий запрос, то проинициализируем левую границу как [math]startL[/math]. Заметим, что все элементы, которые лежат не правее [math]startL[/math], строго меньше текущего искомого элемента, так как они меньше предыдущего запроса, а значит и меньше текущего. Значит инвариант цикла выполнен.

Применение двоичного поиска на некоторых неотсортированных массивах

Задача:

Пусть отсортированный по возрастанию массив из [math]n[/math] элементов [math]a[0 \ldots n - 1][/math], все элементы которого различны, был циклически сдвинут, требуется максимально быстро найти элемент в таком массиве.

Если массив, отсортированный по возрастанию, был циклически сдвнут, тогда полученный массив состоит из двух отсортированных частей. Используем двоичный поиск, чтобы найти индекс последнего элемента левой части массива. Для этого в реализации двоичного поиска заменим условие в if на [math]a[m] \gt a[n-1][/math], тогда в [math]l[/math] будет содержаться искомый индекс:

int l = 0
int r = n + 1    
while l < r - 1                // С помощью бинарного поиска найдем максимум на массиве
    m = (l + r) / 2            // m — середина области поиска
    if a[m] > a[n - 1]         // Сужение границ
        l = m
    else 
        r = m
int x = l                      // x — искомый индекс.

Затем воспользуемся двоичным поиском искомого элемента [math]key[/math], запустив его на той части массива, в которой он находится: на [math][0, x][/math] или на [math][x + 1, n][/math]. Для определения нужной части массива сравним [math]key[/math] с первым и с последним элементами массива:

if key > a[0]               // Если key в левой части
    l = 0
    r = x + 1
if key < a[n]               // Если key в правой части
    l = x + 1
    r = n + 1

Время выполнения данного алгоритма — [math]O(2\log n)=O(\log n)[/math].

Задача:

Массив образован путем приписывания в конец массива, отсортированного по возрастанию, массива, отсортированного по убыванию. Требуется максимально быстро найти элемент в таком массиве.

Найдем индекс последнего элемента массива, отсортированного по возрастанию, воспользовавшись двоичным поиском, условие в if изменим на [math]a[m] \gt a[m - 1][/math]. Тогда в [math]l[/math] будет содержаться искомый индекс:

int l = 0
int r = n + 1    
while l < r - 1                // С помощью бинарного поиска найдем точку экстремума на массиве
    m = (l + r) / 2            // m — середина области поиска
    if a[m] > a[m - 1]         // Проверяем, возрастает ли массив на данном участке
        l = m
    else 
        r = m
int x = l                      // x — искомый индекс.

Затем запустим левосторонний двоичный поиск для каждого массива отдельно: для элементов [math][0 \ldots x][/math] и для элементов [math][x+1 \ldots n][/math]. Для массива, отсортированного по убыванию используем двоичный поиск, изменив условие в if на [math]a[m] \gt key[/math].

Время выполнения алгоритма — [math]O(3\log n)=O(\log n)[/math].

Задача:

Два отсортированных по возрастанию массива записаны один в конец другого. Требуется максимально быстро найти элемент в таком массиве.

Мы имеем массив, образованный из двух отсортированных подмассивов, записанных один в конец другого, запустить сразу бинарный поиск на таком массиве нельзя, так как массив не будет обязательно отсортированным. Также нельзя запустить другие поиски, работающие за [math]O( \log n)[/math], так как неизвестно количество точек экстремума, и нет никакой дополнительной информации об элементах в массивах. Поэтому попробуем найти индекс последнего элемента левого массива, чтобы потом запустить бинарный поиск два раза на отсортированных массивах. Рассмотрим массивы [math] \{ 1,2,3 \mid 4,5,6 \}[/math] и [math] \{ 1,2,3, 4 \mid \textbf{0} ,6 \}[/math] (вертикальная черта означает границу между левым и правым массивами): все элементы, кроме пятого не меняются, значит, по другим элементам невозможно определить, есть ли в правом массиве элемент, который меньше элементов левого массива, поэтому для нахождения конца левого массива придется сравнить все элементы с соседними за [math]O(n)[/math], тогда проще сразу искать нужный элемент, а не конец левого массива.

Для того, чтобы за [math]O(n)[/math] найти элемент в массиве, нужно пройти по всем элементам массива и сравнить их с искомым, быстрее найти элемент в таком массиве нельзя.

Задача:

Массив образован путем циклического сдвига массива, образованного приписыванием отсортированного по убыванию массива в конец отсортированного по возрастанию . Требуется максимально быстро найти элемент в таком массиве.

После циклического сдвига мы получим массив [math]a[0 \ldots n-1][/math], образованный из трех частей: отсортированных по возрастанию-убыванию-возрастанию ([math]\nearrow \searrow \nearrow [/math]) или по убыванию-возрастанию-убыванию ([math] \searrow \nearrow \searrow [/math]). Поэтому с помощью двоичного поиска мы ищем индексы максимального и минимального элементов массива, заменив условие в if на [math]a[m] \gt a[m - 1][/math] (ответ будет записан в [math]l[/math]) или на [math]a[m] \gt a[m + 1][/math] (ответ будет записан в [math]r[/math]) соответственно.

Рассмотрим отдельно ситуацию, если наш массив вида возрастание-убывание-возрастание ([math]\nearrow \searrow \nearrow [/math]). В таком случае может быть неправильно найдено значение максимума ([math]max[/math]). В [math]r[/math] будет храниться изначальное значение, то есть [math]n+1[/math]. Тогда если последний элемент массива меньше первого, нужно еще раз запустить поиск максимума, но уже на промежутке от [math]0[/math] до [math]min[/math].

В случае же убывание-возрастание-убывание ([math] \searrow \nearrow \searrow [/math]) мы неправильно найдем минимум. Найдем правильный минимум аналогично поиску максимума в предыдущем абзаце.

Затем, в зависимости от расположения частей (можно узнать, сравнив [math]min[/math] и [math]max[/math]), запустим двоичный поиск для каждой части отдельно аналогично задаче о поиске элемента на массиве, отсортированном по возрастанию, в конец которого приписан массив, отсортированный по убыванию.

Время выполнения данного алгоритма — [math]O(6\log n)=O(\log n)[/math].

См. также

• Вещественный двоичный поиск
• Троичный поиск
• Поиск с помощью золотого сечения
• Интерполяционный поиск

Источники информации

• Д. Кнут — Искусство программирования (Том 3, 2-е издание)
• Википедия — двоичный поиск
• Интересная статья про типичные ошибки
• Бинарный поиск на algolist