Алгоритм масштабирования потока — различия между версиями
Zemskovk (обсуждение | вклад) м (→Оценка времени работы) |
Zemskovk (обсуждение | вклад) м |
||
| Строка 11: | Строка 11: | ||
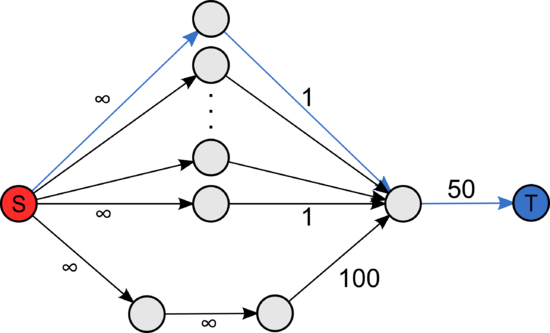
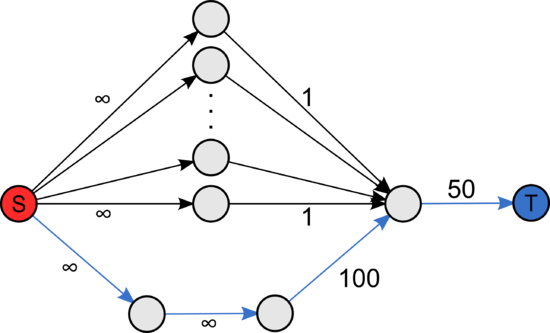
Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью. | Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью. | ||
{|border="0" cellpadding="5" width=30% align=center | {|border="0" cellpadding="5" width=30% align=center | ||
| − | |[[Файл:Flow_scale_1.png| | + | |[[Файл:Flow_scale_1.png|550px|thumb|center|Выбор дополняющих путей в порядке длины]] |
| − | |[[Файл:Flow_scale_2.png| | + | |[[Файл:Flow_scale_2.png|550px|thumb|center|Выбор пути с высокой пропускной способностью в первую очередь]] |
|} | |} | ||
== Оценка времени работы == | == Оценка времени работы == | ||
| + | {{Утверждение | ||
| + | |statement= | ||
| + | Время работы алгоритма {{---}} <tex> O(E^2 \log U) </tex>. | ||
| + | |proof= | ||
| + | В ходе выполнения алгоритма масштаб <tex> \Delta </tex> принимает следующие значения: <tex> S = \{2^{\lfloor \log_2 U \rfloor}, \ldots, 2^k, \ldots, 2, 1, 0\} </tex>. Тогда <tex> |S| = O(\log U) </tex> {{---}} количество итераций алгоритма. | ||
| + | |||
{{Лемма | {{Лемма | ||
|about= | |about= | ||
| Строка 22: | Строка 28: | ||
Максимальный поток в сети <tex> G </tex> ограничен сверху значением <tex> |f_k| + 2^k E </tex>, где <tex> |f_k| </tex> {{---}} значение потока при масштабе <tex> \Delta = 2^k </tex>. | Максимальный поток в сети <tex> G </tex> ограничен сверху значением <tex> |f_k| + 2^k E </tex>, где <tex> |f_k| </tex> {{---}} значение потока при масштабе <tex> \Delta = 2^k </tex>. | ||
|proof= | |proof= | ||
| − | [[Файл:Flow_scale_3.png| | + | [[Файл:Flow_scale_3.png|580px|thumb|right|Разрез <tex> C_k </tex>]] |
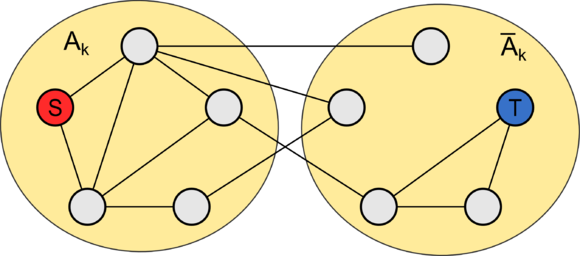
В конце итерации с масштабом <tex> \Delta = 2^k </tex>, сеть <tex> G_{f_k} </tex> может быть разбита на два непересекающихся множества <tex> A_k </tex> и <tex> \overline{A_k} </tex> так, что остаточная пропускная способность каждого ребра, идущего из <tex> A_k </tex> в <tex> \overline{A_k} </tex>, не превосходит масштаба <tex> \Delta </tex>. То есть образуется [[Разрез,_лемма_о_потоке_через_разрез|разрез]] <tex> C_k = \langle A_k, \overline{A_k} \rangle </tex>. | В конце итерации с масштабом <tex> \Delta = 2^k </tex>, сеть <tex> G_{f_k} </tex> может быть разбита на два непересекающихся множества <tex> A_k </tex> и <tex> \overline{A_k} </tex> так, что остаточная пропускная способность каждого ребра, идущего из <tex> A_k </tex> в <tex> \overline{A_k} </tex>, не превосходит масштаба <tex> \Delta </tex>. То есть образуется [[Разрез,_лемма_о_потоке_через_разрез|разрез]] <tex> C_k = \langle A_k, \overline{A_k} \rangle </tex>. | ||
| Строка 37: | Строка 43: | ||
|proof= | |proof= | ||
На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше <tex> 2^k </tex>. | На некоторой итерации алгоритма каждый дополняющий путь имеет пропускную способность не меньше <tex> 2^k </tex>. | ||
| − | Дополняющий поток на предыдущем шаге ограничен значением <tex> 2^{k + 1} E </tex>. Следовательно, на каждой итерации количество дополняющих путей не превосходит <tex> 2E </tex> | + | Дополняющий поток на предыдущем шаге ограничен значением <tex> 2^{k + 1} E </tex>. Следовательно, на каждой итерации количество дополняющих путей не превосходит <tex> 2E </tex>. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Количество итераций алгоритма {{---}} <tex> O(\log U) </tex>, значит, суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. | Количество итераций алгоритма {{---}} <tex> O(\log U) </tex>, значит, суммарное количество увеличивающих путей {{---}} <tex> O(E \log U) </tex>. | ||
| + | }} | ||
| − | Алгоритм [[Обход_в_ширину|обхода в ширину]] находит каждый дополняющий путь за время <tex> O(E) </tex>. Следовательно, суммарное время работы алгоритма {{---}} <tex> O(E^2 \log U) </tex>.}} | + | Алгоритм [[Обход_в_ширину|обхода в ширину]] находит каждый дополняющий путь за время <tex> O(E) </tex>. Следовательно, суммарное время работы алгоритма {{---}} <tex> O(E^2 \log U) </tex>. |
| + | }} | ||
== Псевдокод == | == Псевдокод == | ||
| − | ''' | + | '''function''' maxFlowByScaling(G: '''graph''', s: '''int''', t: '''int'''): '''int''' |
| − | < | + | '''int''' flow = 0 <font color=darkgreen> // поток в сети </font> |
| − | <tex> | + | '''int''' scale = <tex>2^{\lfloor\log_2U\rfloor}</tex> <font color=darkgreen> // текущий минимальный размер потока, который пытаемся пустить </font> |
| − | '''while''' <tex> \ | + | '''while''' scale <tex> \geqslant </tex> 1 |
| − | ''' | + | '''while''' в <tex> G_f </tex> существует увеличивающий путь <tex> p </tex> с пропускной способностью не меньше, чем scale |
| − | + | '''int''' minCapacity = <tex>\min\{c(u, v) \colon(u, v) \in p\} </tex> <font color=darkgreen> // минимальная пропускная способность в увеличивающем пути </font> | |
| − | + | увеличить поток по рёбрам <tex> p </tex> на minCapacity | |
| − | + | обновить <tex> G_f </tex> | |
| − | + | flow = flow + minCapacity | |
| − | + | scale = scale / 2 | |
| − | '''return''' | + | '''return''' flow |
| + | |||
== См. также == | == См. также == | ||
* [[Определение_сети,_потока|Определение сети, потока]] | * [[Определение_сети,_потока|Определение сети, потока]] | ||
Версия 21:36, 2 января 2016
Алгоритм
Пусть дана сеть , все ребра которой имеют целочисленную пропускную способность. Обозначим за максимальную пропускную способность: .
Идея алгоритма заключается в нахождении путей с высокой пропускной способностью в первую очередь, чтобы сразу сильно увеличивать поток по ним, а затем по всем остальным. Для этого воспользуемся масштабом . Изначально положим .
На каждой итерации в дополняющей сети алгоритм находит дополняющие пути с пропускной способностью не меньшей и увеличивает поток вдоль них. Уменьшив масштаб в раза, переходит к следующей итерации.
Очевидно, что при алгоритм вырождается в алгоритм Эдмондса-Карпа, вследствие чего является корректным.
Количество необходимых увеличений путей, основанных на кратчайших путях, может быть много больше количества увеличений, основанных на путях с высокой пропускной способностью.
Оценка времени работы
| Утверждение: | ||||||||||||
Время работы алгоритма — . | ||||||||||||
|
В ходе выполнения алгоритма масштаб принимает следующие значения: . Тогда — количество итераций алгоритма.
| ||||||||||||
Псевдокод
function maxFlowByScaling(G: graph, s: int, t: int): int
int flow = 0 // поток в сети
int scale = // текущий минимальный размер потока, который пытаемся пустить
while scale 1
while в существует увеличивающий путь с пропускной способностью не меньше, чем scale
int minCapacity = // минимальная пропускная способность в увеличивающем пути
увеличить поток по рёбрам на minCapacity
обновить
flow = flow + minCapacity
scale = scale / 2
return flow