Двоичный каскадный сумматор — различия между версиями
(→Принцип работы) |
|||
| Строка 19: | Строка 19: | ||
Поскольку последовательное применение этих трёх действий над переносами принадлежит также одному из этих типов, то можно определить композицию действий над переносами. Обозначим композицию значком <tex>\otimes</tex> и построим таблицу значений (в столбце первый аргумент, в строке — второй): | Поскольку последовательное применение этих трёх действий над переносами принадлежит также одному из этих типов, то можно определить композицию действий над переносами. Обозначим композицию значком <tex>\otimes</tex> и построим таблицу значений (в столбце первый аргумент, в строке — второй): | ||
[[Файл:Пример компазиции.png|right|450px|thumb|Пример композиции]] | [[Файл:Пример компазиции.png|right|450px|thumb|Пример композиции]] | ||
| − | {| | + | {| class="wikitable" align="center" style="color: blue; background-color:#ccffcc;" cellpadding="3" |
| − | + | !colspan="20"|Таблица значений | |
| − | + | |-align="center" | |
| − | + | | <tex>\otimes</tex> || <tex>k</tex> || <tex>p</tex> || <tex>g</tex> | |
| − | + | |-align="center" | |
| − | + | | <tex>k</tex> || <tex>k</tex> || <tex>k</tex> || <tex>g</tex> | |
| − | + | |-align="center" | |
| − | + | | <tex>p</tex> || <tex>k</tex> || <tex>p</tex> || <tex>g</tex> | |
| − | + | |-align="center" | |
| − | + | | <tex>g</tex> || <tex>k</tex> || <tex>g</tex> || <tex>g</tex> | |
| − | + | |-align="center" | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Поскольку функция ассоциативна, то можно распространить её на любое количество аргументов. Более того, поскольку для любого действия <tex>x</tex> выполняется равенство <tex>x \otimes p = x</tex>, то функцию от нескольких действий можно определить как "последнее не <tex>p</tex>". | Поскольку функция ассоциативна, то можно распространить её на любое количество аргументов. Более того, поскольку для любого действия <tex>x</tex> выполняется равенство <tex>x \otimes p = x</tex>, то функцию от нескольких действий можно определить как "последнее не <tex>p</tex>". | ||
Версия 01:00, 19 января 2016
| Определение: |
| Двоичный каскадный сумматор - Binary adder — цифровая схема, осуществляющая сложение двух многоразрядных двоичных чисел, с ускоренным формированием разрядов переноса. |
Принцип работы
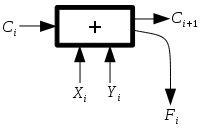
Используемые обозначения: — -ый разряд суммируемых чисел, — биты переноса, — результат сложения.
Рассмотрим один элемент линейного каскадного сумматора - Ripple-carry adder. В некоторых случаях бит переноса зависит только от значений и :
- если , то ,
- если , то ;
Иначе () бит переноса не изменяется, то есть .
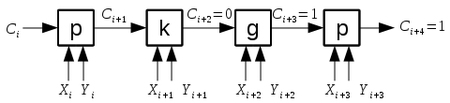
Три случая называются следующим образом:
- — "порождение" переноса,
- — "уничтожение" переноса,
- — "проталкивание" переноса;
Поскольку последовательное применение этих трёх действий над переносами принадлежит также одному из этих типов, то можно определить композицию действий над переносами. Обозначим композицию значком и построим таблицу значений (в столбце первый аргумент, в строке — второй):
| Таблица значений | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Поскольку функция ассоциативна, то можно распространить её на любое количество аргументов. Более того, поскольку для любого действия выполняется равенство , то функцию от нескольких действий можно определить как "последнее не ".
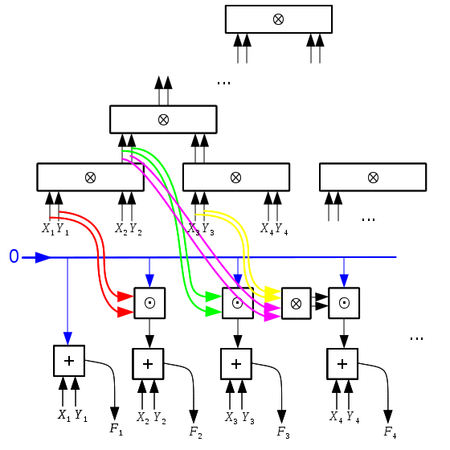
Схема
Сумматор состоит из двух частей. Первая часть — это группа полных сумматоров, вычисляющих ответ. Вторая часть — дерево отрезков, с помощью которого вычисляется бит переноса.
Обозначения
- — полный сумматор, вычисляет результат сложения.
- — блок вычисления композиции двух переносов.
- — блок вычисления , старшего бита сумматора.
Схемная сложность
Дерево отрезков вычисляет биты переноса за , оставшиеся действия выполняются за . Суммарное время работы — .
Источники информации