Рёберное ядро — различия между версиями
(→Реберное ядро в двудольном графе) |
(→Критерий существования реберного ядра) |
||
| Строка 35: | Строка 35: | ||
Докажем <tex>(2) \Rightarrow (1)</tex>. | Докажем <tex>(2) \Rightarrow (1)</tex>. | ||
Пусть <tex>M = \{v_1, \dots, v_s\}</tex> {{---}} наименьшее внешнее вершинное покрытие. Пусть <tex>Y_i = \{u \mid u \in U, uv_i \in E(G) \}</tex>. Тогда для любого <tex>k: \:\: 1 \leqslant k \leqslant s</tex>, объединение любых <tex>k</tex> различных множеств <tex>Y_i</tex> содержит, по меньшей мере <tex>k</tex> вершин. | Пусть <tex>M = \{v_1, \dots, v_s\}</tex> {{---}} наименьшее внешнее вершинное покрытие. Пусть <tex>Y_i = \{u \mid u \in U, uv_i \in E(G) \}</tex>. Тогда для любого <tex>k: \:\: 1 \leqslant k \leqslant s</tex>, объединение любых <tex>k</tex> различных множеств <tex>Y_i</tex> содержит, по меньшей мере <tex>k</tex> вершин. | ||
| − | Следовательно, по теореме Холла | + | Следовательно, по теореме Холла<ref>P. Hall "On representatives of subsets" [https://math.dartmouth.edu/archive/m38s12/public_html/sources/Hall1935.pdf]</ref>, существует множество <tex>s</tex> различных вершин <tex>\{y_1, \dots, y_s\}, \: y_j \in Y_j</tex>. Следовательно существует набор независимых ребер <tex>y_1v_1, \dots, y_sv_s</tex>. А значит <tex>C_1(G)</tex> не может быть пустым. |
}} | }} | ||
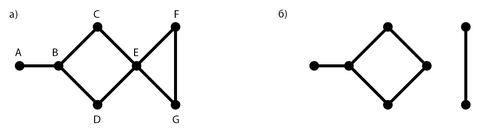
[[Файл:EdgeCore.png|thumb|500px|рис. 1. a) граф <tex>H</tex>, б) реберное ядро графа <tex>H</tex> ]] | [[Файл:EdgeCore.png|thumb|500px|рис. 1. a) граф <tex>H</tex>, б) реберное ядро графа <tex>H</tex> ]] | ||
Версия 14:09, 28 января 2016
| Определение: |
| Рёберное ядро (англ. core) графа — это подграф графа , порожденный объединением таких независимых множеств , что , где — число вершинного покрытия. |
| Определение: |
| Множество ребер (вершин) называется независимым (англ. independent), если никакие его два элемента не смежны. |
| Определение: |
| Вершинным покрытием (англ. vertex cover) графа называется такое множество его вершин, что у любого ребра в хотя бы одна из вершин лежит в . |
| Определение: |
| числом вершинного покрытия (англ. point-covering number) называется число вершин в наименьшем вершинном покрытии графа . |
Критерий существования реберного ядра
| Определение: |
| Наименьшее вершинное покрытие M графа G с множеством вершим V называется внешним (англ. external vertex cover), если для любого подмножества выполняется неравнство , где . |
| Теорема: |
для произвольного графа следующие утверждения эквивалентны:
(1) имеет не пустое рёберное ядро. |
| Доказательство: |
|
Обозначим минимальное вершинное покрытие как . Пусть . |
В качестве примера рассмотрим граф изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: и .
Пусть то . Пусть . Тогда .
Отсюда и . И это верно для любого подмножества . Значит, — внешнее покрытие. Значит и — внешнее покрытие.
Реберное ядро в двудольном графе
Здесь и далее будем рассматривать двудольный граф , в котором обозначим — множество вершин левой доли, — множество вершин правой доли.
| Определение: |
| — полунесводимый граф, если имеет ровно одно вершинное покрытие , такое что или или — пусто |
| Определение: |
| — несводимый граф, если он имеет ровно два наименьших вершинных покрытия и , таких что либо , либо |
| Определение: |
| — сводимый граф если он не является ни полунесводимым, ни сводимым. |
| Теорема: |
Если оба конца ребра покрыто некоторым минимальным вершинным покрытием, то . |
Следствие 1 если имеет минимальное вершинное покрытие, которое не является независимым, то .
Следствие 2 если — сводимый связный двудольный граф, то .
| Теорема: |
если имеет непустое реберное ядро, то , , а компоненты являются несводимыми или полунесводимыми двудольными подграфами |
| Теорема: |
и его реберное ядро совпадают тогда и только тогда, когда является двудольным и не является сводимым. |
| Доказательство: |
|
Пусть тогда по предыдущей теореме является несводимым или полунесводимым двудольным графом. |