Произвольно вычерчиваемые из заданной вершины графы — различия между версиями
м |
|||
| Строка 2: | Строка 2: | ||
|definition= | |definition= | ||
[[Основные определения теории графов|Граф]] называется '''произвольно вычерчиваемым из вершины <tex>v</tex>''' (англ. ''Arbitrarily traceable graph''), если любая цепь с началом в вершине <tex>v</tex> может быть продолжена до эйлерового цикла графа <tex>G</tex>. }} | [[Основные определения теории графов|Граф]] называется '''произвольно вычерчиваемым из вершины <tex>v</tex>''' (англ. ''Arbitrarily traceable graph''), если любая цепь с началом в вершине <tex>v</tex> может быть продолжена до эйлерового цикла графа <tex>G</tex>. }} | ||
| − | + | {{Утверждение | |
| + | |statement=Любой произвольно вычерчиваемый из вершины <tex>v</tex> граф является [[Эйлеров цикл, Эйлеров путь, Эйлеровы графы, Эйлеровость орграфов|эйлеровым графом]]. | ||
| + | }} | ||
{{Теорема | {{Теорема | ||
| Строка 8: | Строка 10: | ||
[[Эйлеров цикл, Эйлеров путь, Эйлеровы графы, Эйлеровость орграфов|Эйлеров граф]] <tex>G</tex>, содержащий хотя бы одно ребро, является произвольно вычерчиваемым из вершины <tex>v</tex> <tex>\Longleftrightarrow</tex> вершина <tex>v</tex> принадлежит всем циклам графа <tex>G</tex>.<br> | [[Эйлеров цикл, Эйлеров путь, Эйлеровы графы, Эйлеровость орграфов|Эйлеров граф]] <tex>G</tex>, содержащий хотя бы одно ребро, является произвольно вычерчиваемым из вершины <tex>v</tex> <tex>\Longleftrightarrow</tex> вершина <tex>v</tex> принадлежит всем циклам графа <tex>G</tex>.<br> | ||
|proof= | |proof= | ||
| − | [[Файл:ATG_part1.jpg| | + | [[Файл:ATG_part1.jpg|200px|right]] |
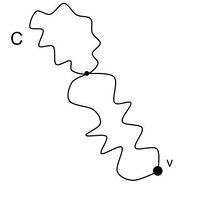
| − | <tex>\Rightarrow</tex> Пусть в <tex>G</tex> <tex>\exists</tex> цикл <tex>C, v \notin C</tex>.<br> | + | <tex>\Rightarrow</tex> |
| + | Пусть в <tex>G</tex> <tex>\exists</tex> цикл <tex>C, v \notin C</tex>.<br> | ||
Рассмотрим <tex>G_1 = G/C</tex> (здесь и далее это означает удаление только ребер, не трогая вершины). При удалении цикла все степени вершин остались четными, потому что каждая вершина содержит четное количество ребер цикла, и следовательно <tex>G_1</tex> {{---}} эйлеров. Тогда в <tex>G_1</tex> <tex>\exists</tex> эйлеров цикл. Если начать обход по эйлерову циклу из <tex>v</tex>, то и закончится он в <tex>v</tex>. Если теперь вернуть цикл <tex>C</tex>, то мы никак не сможем его обойти, так как из вершины <tex>v</tex> больше нет не посещенных ребер <tex>\Rightarrow</tex> <tex>G</tex> не свободно вычерчиваемый из <tex>v</tex>. | Рассмотрим <tex>G_1 = G/C</tex> (здесь и далее это означает удаление только ребер, не трогая вершины). При удалении цикла все степени вершин остались четными, потому что каждая вершина содержит четное количество ребер цикла, и следовательно <tex>G_1</tex> {{---}} эйлеров. Тогда в <tex>G_1</tex> <tex>\exists</tex> эйлеров цикл. Если начать обход по эйлерову циклу из <tex>v</tex>, то и закончится он в <tex>v</tex>. Если теперь вернуть цикл <tex>C</tex>, то мы никак не сможем его обойти, так как из вершины <tex>v</tex> больше нет не посещенных ребер <tex>\Rightarrow</tex> <tex>G</tex> не свободно вычерчиваемый из <tex>v</tex>. | ||
| − | [[Файл:ATG_part2.jpg| | + | [[Файл:ATG_part2.jpg|200px|right]] |
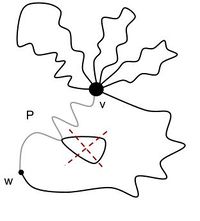
| − | <tex>\Leftarrow</tex> Пусть дан эйлеров граф <tex>G</tex>, вершина <tex>v</tex> принадлежит всем его циклам.<br> | + | <tex>\Leftarrow</tex> |
| + | Пусть дан эйлеров граф <tex>G</tex>, вершина <tex>v</tex> принадлежит всем его циклам.<br> | ||
Рассмотрим произвольный путь <tex>P = v \leadsto w</tex>. Пусть <tex>G_1 = G/P</tex>. Возможны 2 случая: | Рассмотрим произвольный путь <tex>P = v \leadsto w</tex>. Пусть <tex>G_1 = G/P</tex>. Возможны 2 случая: | ||
| Строка 24: | Строка 28: | ||
== Строение == | == Строение == | ||
| − | [[Файл:ATGexample.jpg|right| | + | [[Файл:ATGexample.jpg|right|300px]] |
Опираясь на теорему опишем строение всех графов, произвольно вычерчиваемых из вершины <tex>v</tex>. <br> | Опираясь на теорему опишем строение всех графов, произвольно вычерчиваемых из вершины <tex>v</tex>. <br> | ||
Возьмем произвольный [[Дерево, эквивалентные определения|лес]] <tex>H</tex>, не содержащий вершину <tex>v</tex>. Каждую вершину нечетной степени соединим некоторым нечетным числом кратных ребер с <tex>v</tex>, а каждую вершину четной степени <tex>-</tex> четным числом кратных ребер с <tex>v</tex> (не исключая <tex>0</tex>), причем каждую изолированную вершину обязательно соединим с <tex>v</tex>.<br> | Возьмем произвольный [[Дерево, эквивалентные определения|лес]] <tex>H</tex>, не содержащий вершину <tex>v</tex>. Каждую вершину нечетной степени соединим некоторым нечетным числом кратных ребер с <tex>v</tex>, а каждую вершину четной степени <tex>-</tex> четным числом кратных ребер с <tex>v</tex> (не исключая <tex>0</tex>), причем каждую изолированную вершину обязательно соединим с <tex>v</tex>.<br> | ||
| − | Полученный граф <tex>G</tex>: связен, имеет только вершины четной степени | + | Полученный граф <tex>G</tex>: |
| + | * связен, | ||
| + | * имеет только вершины четной степени, | ||
| + | * является произвольно вычерчиваемым из <tex>v</tex>, как эйлеров граф, у которого <tex>v</tex> принадлежит всем циклам. | ||
Теперь докажем, почему таким образом можно получить все графы, произвольно вычерчиваемые из вершины <tex>v</tex>. Пусть какой-то такой граф нельзя получить методом описанным выше. Тогда уберем все ребра из вершины <tex>v</tex> и посмотрим на граф, который остался. Он не является лесом, иначе мы могли бы получить этот граф нашим методом. Но если он не является лесом, то в нем есть хотя бы один цикл, который не содержит <tex>v</tex>. А по теореме о произвольно вычерчиваемымых из вершины графах такого быть не может. Следовательно наше предположение ошибочно. | Теперь докажем, почему таким образом можно получить все графы, произвольно вычерчиваемые из вершины <tex>v</tex>. Пусть какой-то такой граф нельзя получить методом описанным выше. Тогда уберем все ребра из вершины <tex>v</tex> и посмотрим на граф, который остался. Он не является лесом, иначе мы могли бы получить этот граф нашим методом. Но если он не является лесом, то в нем есть хотя бы один цикл, который не содержит <tex>v</tex>. А по теореме о произвольно вычерчиваемымых из вершины графах такого быть не может. Следовательно наше предположение ошибочно. | ||
Версия 21:40, 28 января 2016
| Определение: |
| Граф называется произвольно вычерчиваемым из вершины (англ. Arbitrarily traceable graph), если любая цепь с началом в вершине может быть продолжена до эйлерового цикла графа . |
| Утверждение: |
Любой произвольно вычерчиваемый из вершины граф является эйлеровым графом. |
| Теорема: |
Эйлеров граф , содержащий хотя бы одно ребро, является произвольно вычерчиваемым из вершины вершина принадлежит всем циклам графа . |
| Доказательство: |
|
Пусть в цикл .
Пусть дан эйлеров граф , вершина принадлежит всем его циклам.
Покажем, что в обоих случаях эйлеров обход пройдет по всем ребрам . В единственная компонента связности, содержащая ребра. При удалении их количество не могло увеличится, иначе должен быть цикл, не содержащий (смотри рисунок). Значит в единственная компонента связности содержащая ребра, причем либо полуэйлеров, либо эйлеров в эйлерова цепь эйлеров цикл в графе . |
Строение
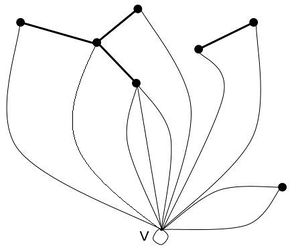
Опираясь на теорему опишем строение всех графов, произвольно вычерчиваемых из вершины .
Возьмем произвольный лес , не содержащий вершину . Каждую вершину нечетной степени соединим некоторым нечетным числом кратных ребер с , а каждую вершину четной степени четным числом кратных ребер с (не исключая ), причем каждую изолированную вершину обязательно соединим с .
Полученный граф :
- связен,
- имеет только вершины четной степени,
- является произвольно вычерчиваемым из , как эйлеров граф, у которого принадлежит всем циклам.
Теперь докажем, почему таким образом можно получить все графы, произвольно вычерчиваемые из вершины . Пусть какой-то такой граф нельзя получить методом описанным выше. Тогда уберем все ребра из вершины и посмотрим на граф, который остался. Он не является лесом, иначе мы могли бы получить этот граф нашим методом. Но если он не является лесом, то в нем есть хотя бы один цикл, который не содержит . А по теореме о произвольно вычерчиваемымых из вершины графах такого быть не может. Следовательно наше предположение ошибочно.
См. также
Источники информации
- Асанов М., Баранский В., Расин В. Дискретная математика: Графы, матроиды, алгоритмы., Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001. ISBN 5-93972-076-5