Суффиксный автомат

Определение:

Суффиксный автомат (англ. suffix automaton, directed acyclic word graph) — минимальный ДКА, который принимает все суффиксы строки и только их.

Описание

Суффиксный автомат [math]A[/math] для строки [math]s[/math] представляет собой ациклический ориентированный граф, с начальной вершиной и множеством терминальных вершин, рёбра которого помечены символами [math]s[/math].

Пример суффиксного автомата для строки [math]abbab[/math].

Определение:

Состояние [math]q[/math] принимает строку [math]s[/math], если существует путь из начального состояния в [math]q[/math], такой, что если последовательно выписать буквы на рёбрах на пути, получим строку [math]s[/math].

Определение:

Автомат принимает строку [math]s[/math], если её принимает хотя бы одно из финальных состояний.

Так как автомат детерминированный, то каждому пути соответствует строка.

Если две строки [math]a[/math] и [math]b[/math] принимаются одним состоянием [math]q[/math] произвольного автомата, то для любой строки [math]x[/math] строки [math]ax[/math] и [math]bx[/math] принимаются или не принимаются автоматом одновременно. Действительно, независимо от того, как мы пришли в состояние [math]q[/math], если мы пройдём из него по пути, соответствующему строке [math]x[/math], мы сможем точно сказать, в какое состояние мы попадём (в частности, будет ли оно финальным). Значит, любому состоянию [math]q[/math] соответствует множество строк [math]X_q[/math], которые переводят его в одно из конечных состояний.

Определение:

Множество [math]X_q[/math] называют правым контекстом состояния.

Правый контекст определен не только для состояния, но и для строк, которые оно принимает — правый контекст строк совпадает с правым контекстом состояния.

Утверждение:

Состояний в автомате не меньше, чем различных правых контекстов у подстрок строки, для которой он построен, причём в минимальном автомате достигается нижняя оценка.

[math]\triangleright[/math]

Допустим, что в автомате есть два состояния [math]q_1[/math] и [math]q_2[/math] такие что [math]X_{q_1} = X_{q_2}[/math]. Мы можем удалить состояние [math]q_2[/math] и перевести переходы, ведущие в него в состояние [math]q_1[/math]. Множество принимаемых строк от этого не изменится, следовательно, мы можем продолжать, пока количество состояний не будет равно числу попарно различных правых контекстов.

[math]\triangleleft[/math]

Таким образом, ДКА является минимальным тогда и только тогда, когда правые контексты всех его состояний попарно различны. В случае суффиксного автомата правый контекст [math]X_a[/math] строки [math]a[/math] взаимнооднозначно соответствует множеству правых позиций вхождений строки [math]a[/math] в строку [math]s[/math]. Таким образом, каждое состояние автомата принимает строки с одинаковым множеством правых позиций их вхождений и обратно, все строки с таким множеством позиций принимается этим состоянием.

Построение

Алгоритм

Определение:

Пусть длина самой короткой строки, которая принимается состоянием [math]q[/math] равно [math]k[/math], тогда суффиксная ссылка [math]link_q[/math] будет вести из этого состояния в состояние, которое принимает эту же строку без первого символа.

Будем обозначать длину самой длинной строки, которая принимается состоянием [math]q[/math] как [math]len_q[/math]. Длина самой короткой строки из [math]q[/math] в таком случае будет равна [math]len(link_q) + 1[/math]. Суффиксный автомат может быть построен за линейное время online-алгоритмом. Будем добавлять символы строки [math]s[/math] по одному, перестраивая при этом автомат. Изначально автомат состоит из одного состояния, для которого [math]len(0) = 0[/math], а [math]link_0 = -1[/math].
Обозначим состояние [math]last[/math], соответствующее текущей строке до добавления символа [math]c[/math] (изначально [math]last = 0[/math]).
Создадим новое состояние [math]cur[/math], [math]len(cur) = len(last) + 1[/math].
Рассмотрим все переходы из [math]last[/math] по текущему символу [math]c[/math]. Если перехода нет, то добавляем переход в [math]cur[/math], переходим по суффиксной ссылке и повторяем процедуру снова. Если переход существует, то остановимся и обозначим текущее состояние за [math]p[/math]. Если перехода не нашлось и по суффиксным ссылкам мы дошли до фиктивного состояния (на которое указывает [math]link_0[/math]), то [math]link_{cur} = 0[/math].
Допустим, что мы остановились в состоянии [math]p[/math], из которого существует переход с символом [math]c[/math]. Обозначим состояние, куда ведёт переход, через [math]q[/math]. Рассмотрим два случая:

1. Если [math]len(p) + 1 = len(q)[/math], то [math]link(q) = cur[/math].
   
2. В противном случае, создадим новое состояние [math]new[/math], скопируем в него [math]q[/math] вместе с суффиксными ссылками и переходами. [math]len(new)[/math] присвоим значение [math]len(p) + 1[/math]. Перенаправим суффиксную ссылку из [math]q[/math] в [math]new[/math] и добавим ссылку из [math]cur[/math] в [math]new[/math]. Пройдём по всем суффиксным ссылкам из состояния [math]p[/math] и все переходы в состояние [math]q[/math] по символу [math]c[/math] перенаправим в [math]new[/math].

Обновим значение [math]last = cur[/math].

Пример построения

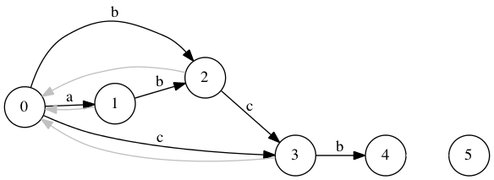
Рассмотрим построение суффиксного автомата для строки [math]abcb[/math]. Серыми стрелками показаны суффиксные ссылки.

1. Изначально автомат состоит из одного начального состояния. [math]last = 0, len(0) = 0[/math].
   
   
   

   Шаг 1.
   
   
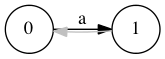
2. Добавляем символ [math]a[/math]. Создаем состояние [math]1[/math]. Переходов из начального состояния по символу [math]a[/math] нет, перейти по суффиксным ссылкам некуда, значит добавим суффиксную ссылку [math]link_{1} = 0[/math]. [math]last = 1, len(1) = 1[/math].
   
   
   

   Шаг 2.
   
   
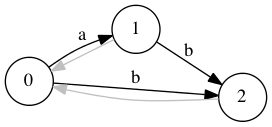
3. Добавляем символ [math]b[/math]. Создаем состояние [math]2[/math]. Добавим переход из [math]1[/math], откатимся по суффиксной ссылке и добавим переход из [math]0[/math]. Добавим суффиксную ссылку [math]link_{2} = 0[/math]. [math]last = 2, len(2) = 2[/math].
   
   
   

   Шаг 3.
   
   
4. Аналогично добавим символ [math]c[/math] и обновим автомат. [math]last = 3, len(3) = 3[/math].
   
   
   

   Шаг 4.
   
   
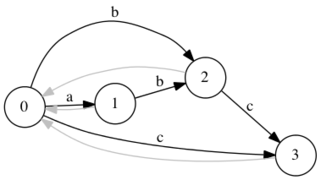
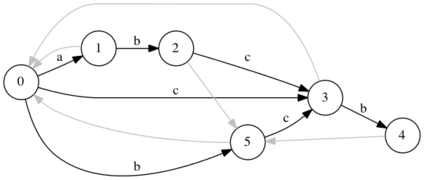
5. Добавляем символ [math]b[/math]. Добавим переход из [math]3[/math] и перейдем по суффиксной ссылке в начальное состояние. Из состояния [math]0[/math] существует переход по символу [math]b[/math].
   
   
   

   Шаг 5.
   
   
6. Рассмотрим состояние [math]2[/math], куда существует переход. Имеем [math]len(0) + 1 \neq len(2)[/math].
   1. Создаем новое состояние [math]5[/math].
   2. Копируем в него все суффиксные ссылки и переходы из [math]2[/math] и присвоим [math]len(5) = len(0) + 1 = 1[/math].
   3. Перенаправим суффиксную ссылку из [math]2[/math] в [math]5[/math] и добавим ссылку из [math]4[/math] в [math]5[/math]. Перенаправим переход [math]0 \rightarrow 2[/math] в состояние [math]5[/math].
      
      
      

      Шаг 6.
      
      
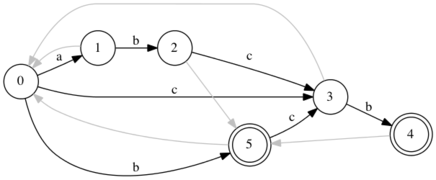
7. Построение автомата завершено. Чтобы пометить терминальные вершины, найдём состояние, которое принимает строку [math]abcb[/math] и пройдём по суффиксным ссылкам, помечая все посещенные состояния терминальными.
   
   
   

   Шаг 7.

Реализация

• Переходы хранятся в массиве отображений (ключ — символ, значение — номер состояния) [math]edges[/math],
• Суффиксные ссылки хранятся в массиве [math]link[/math],
• Длины строк хранятся в массиве [math]len[/math],
• Функция [math]newState[/math] создаёт новое состояние и возвращает его номер,
• Функция [math]clone[/math] копирует состояние и возвращает номер нового состояния.

func addChar(c):
    cur = newState()                                       // создаём новое состояние и возвращаем его номер 

    p = last
    while p >= 0 and edges[p].find(c) == edges[p].end():
        edges[p][c] = cur
        p = link[p]

    if p != -1:
        q = edges[p][c]
        if len[p] + 1 == len[q]:
            link[cur] = q
        else:
            new = clone(q)                                // скопируем состояние [math]q[/math]
            len[new] = len[p] + 1
            link[q] = link[cur] = new
            while p >= 0 and edges[p][c] == q:
                edges[p][c] = new
                p = link[p]
    last = cur

Источники информации

• Maxime Crochemore, Christophe Hancart, Thierry Lecroq — Algorithms on Strings
• А. Кульков — Лекция по суффиксным структурам
• MAXimal :: algo :: Суффиксный автомат