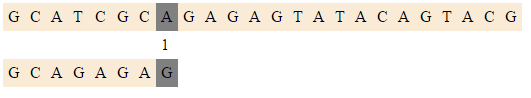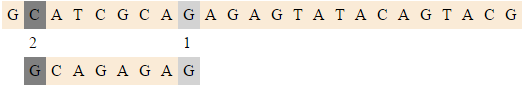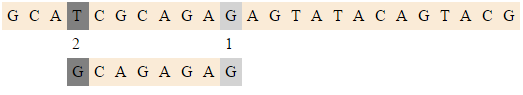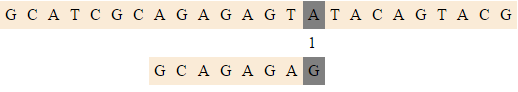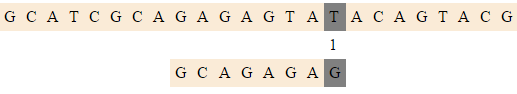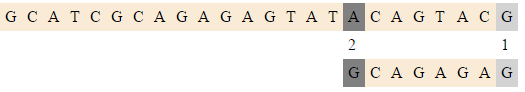Алгоритм Райта — различия между версиями
Zernov (обсуждение | вклад) (→Псевдокод) |
Zernov (обсуждение | вклад) (→Пример) |
||
| Строка 86: | Строка 86: | ||
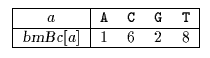
Пусть нам дана строка <tex>y = GCATCGCAGAGAGTATACAGTACG</tex> и образец <tex>x=GCAGAGAG</tex> | Пусть нам дана строка <tex>y = GCATCGCAGAGAGTATACAGTACG</tex> и образец <tex>x=GCAGAGAG</tex> | ||
| − | [[Файл:RaitaPre.png|thumb| | + | [[Файл:RaitaPre.png|thumb|left|300px|Массив <tex>bmBc</tex> после фазы препроцессинга]] |
| + | |||
| + | Рассмотрим шаги алгоритма: | ||
{| class = "wikitable" | {| class = "wikitable" | ||
! Изображение !! <tex>(j, bmBc[y[j]])</tex> !! Описание | ! Изображение !! <tex>(j, bmBc[y[j]])</tex> !! Описание | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita1.png|550px]] | |[[Файл:Raita1.png|550px]] | ||
|<tex>(7, 1)</tex> | |<tex>(7, 1)</tex> | ||
|Делаем сравнение последних символов, оно неудачно, сдвигаемся. | |Делаем сравнение последних символов, оно неудачно, сдвигаемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita2.png|550px]] | |[[Файл:Raita2.png|550px]] | ||
|<tex>(8, 2)</tex> | |<tex>(8, 2)</tex> | ||
|Последние символы совпали, сравниваем первые, сдвигаемся. | |Последние символы совпали, сравниваем первые, сдвигаемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita3.png|550px]] | |[[Файл:Raita3.png|550px]] | ||
|<tex>(10, 2)</tex> | |<tex>(10, 2)</tex> | ||
|Последние символы совпали, сравниваем первые, сдвигаемся. | |Последние символы совпали, сравниваем первые, сдвигаемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita4.png|550px]] | |[[Файл:Raita4.png|550px]] | ||
|<tex>(12, 2)</tex> | |<tex>(12, 2)</tex> | ||
|Совпали последний, первый и средний символы, пробегаемся по всему шаблону и сравниваем символы. Нашли строчку в тексте. Продолжим работу (для примера, в обычном варианте на этом этапе мы можем выйти, если требуется найти только одно вхождение) и сдвинемся. | |Совпали последний, первый и средний символы, пробегаемся по всему шаблону и сравниваем символы. Нашли строчку в тексте. Продолжим работу (для примера, в обычном варианте на этом этапе мы можем выйти, если требуется найти только одно вхождение) и сдвинемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita5.png|550px]] | |[[Файл:Raita5.png|550px]] | ||
|<tex>(14, 1)</tex> | |<tex>(14, 1)</tex> | ||
|Делаем сравнение последних символов, оно неудачно, сдвигаемся. | |Делаем сравнение последних символов, оно неудачно, сдвигаемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita6.png|550px]] | |[[Файл:Raita6.png|550px]] | ||
|<tex>(15, 8)</tex> | |<tex>(15, 8)</tex> | ||
|Делаем сравнение последних символов, оно неудачно, сдвигаемся. | |Делаем сравнение последних символов, оно неудачно, сдвигаемся. | ||
| − | |-align=" | + | |-align="center" |
|[[Файл:Raita7.png|550px]] | |[[Файл:Raita7.png|550px]] | ||
|<tex>(23, 2)</tex> | |<tex>(23, 2)</tex> | ||
Версия 00:30, 31 марта 2016
Алгоритм Райта (англ. Raita algorithm) — алгоритм поиска подстроки в строке, который опубликовал Тим Райта в 1991 году, являющийся модификацией алгоритма Бойера-Мура и улучшающий его асимптотику
Содержание
Описание алгоритма
Алгоритм Райта ищет образец в заданном тексте сравнивания их символы. Сравнение происходит в следующем порядке (окном текста будем называть последовательность символов , где — длина образца ):
- Последний символ образца сравнивается с самым правым символом окна.
- Если они совпадают, то первый символ сравнивается с самым левым символом окна.
- Если они опять совпали, то сравниваются символы, находящиеся посередине образца и окна.
Если все шаги прошли успешно, то начинаем сравнивать образец и текст посимвольно в обычном порядке, начиная с второго с конца символа. В противном случае, выполняем функцию сдвига плохого символа, которая обрабона в стадии препроцессинга. Эта функция аналогична той, которая была использована в фазе препроцессинга алгоритма Бойера-Мура. Кроме того, в третьем шаге можно брать не средний символ, а случайный, либо с каким-то определенным индексом, в зависимости от специфики текста.
Псевдокод
Функция поиска индекса первого вхождения сивола в массиве с позиции до позиции :
int findFirst(char[] y, int fromIndex, int toIndex, char symbol):
for (i = fromIndex .. toIndex)
if (y[i] == symbol)
return i
return -1
Проверка, что все символы в с позиции и до и с начала и до конца совпадают:
boolean restEquals(char[] y, int fromIndex, char[] x, int toIndex):
for (i = fromIndex .. toIndex)
if (y[i] != x[i - fromIndex])
return false
return true
Стадия препроцессинга (совпадает со стадией препроцессинга в алгоритме Бойера-Мура):
int[] preBmBc(char[] x, int m):
int[] result = int[ASIZE]
//Где ASIZE — размер алфавита
for (i = 0 .. ASIZE - 1)
result[i] = m;
for (i = 0 .. m - 2)
result[x[i]] = m - i - 1;
return result
Основная стадия алгоритма:
void RAITA(char[] x, int m, char[] y, int n):
int[] bmBc
char c, firstCh, middleCh, lastCh;
if (m == 0)
return
else if (m == 1)
//Проверка на случай поиска вхождения одного символа
int match = 0
while (match < n)
match = findFirst(y, match, n - 1, x[0])
if (match != -1)
print(match)
else
print("No matches")
return
//Вычисление массива плохих сиволов и объявление первого, последнего и среднего сиволов
bmBc = preBmBc (x, m)
firstCh = x[0];
middleCh = x[m/2];
lastCh = x[m - 1];
//Поиск
int j = 0
while (j <= n - m)
c = y[j + m - 1]
if (lastCh == c && middleCh == y[j + m / 2] && firstCh == y[j] && //Совпадение шаблона и окна из текста
restEquals(y, j + 1, x, j + m - 2))
print(j)
return
j += bmBc[c];
print("No matches")
Асимптотика
- Фаза препроцессинга требует времени и памяти, где — размер алфавита.
- В худшем случае поиск требует сравнений.
Пример: текст, состоящий только из букв и образец . В таком случае, будет равен , то есть после каждой фазы сравнений мы будем сдвигаться на . Значит, всего будет фаз сравнений, а каждая фаза будет работать за , поскольку расхождение будет только в с конца символе, то мы сравним сначала последний, потом первый, потом средний, а затем пойдем с самого начала, сравнивая все символы подряд. Итого получаем асимптотику
- В лучшем случае требует сравнений.
Пример: текст, вида и образец . В таком случае, будет равен . Значит, всего будет не более чем фаз сравнений, а каждая фаза (кроме той, в которой мы нашли вхождение строки) будет работать за , поскольку расхождение будет уже в последних символах. Итого получаем асимптотику
Сравнение с Алгоритмом Бойера-Мура
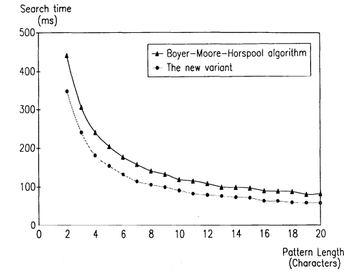
В своей статье Тим Райта экспериментально проверил ускорение алгоритма на реальных текстах. Тесты были приведены на техническом отчете, написанном на английском языке. Длина текста составила символов. Использовался ASCII алфавит (подразумевается теоритический размер алфавита, равный , в тексте было использовано только символов.) Шаблоны длиной случайно выбирались из текста, а затем проходил их поиск в тексте. (См. рисунок)
Результат показывает ускорение модификации алгоритма на относительно оригинального на всех шаблонах. Шаблон встречался в тексте как минимум один раз (из-за метода его выбора). Однако, результаты теста на шаблонах, которые не встречались в тексте, были очень похожи на верхнюю кривую. Очевидно, что шаблоны, имеющие часто встречающиеся суффиксы, такие как или вносят наибольший вклад в быстродействие модификации. (В алгоритме Бойера-Мура мы будем идти с конца, пока не найдем различия, то есть произведем сравнение на всем суффиксе, в то время как в алгоритме Райта мы выйдем сразу после несовпадения первых символов).
Кроме того, производительность растет с увеличением , поскольку вклад сравнений первого, последнего и среднего символа уменьшается. С другой стороны, производительность ухудшается с уменьшением размера алфавита, поскольку вероятность того, что первый, средний и последний символ из шаблона и текста совпадут, увеличивается. Однако, Тим Райт в своей статье пишет, что несмотря на теоритическую возможность ухудшения, на практике, скорее всего, разница будет заметна лишь на очень маленьких алфавитах (например, длины )
Пример
Пусть нам дана строка и образец
Рассмотрим шаги алгоритма:
В итоге, чтобы найти одно вхождение образца длиной в образце длиной нам понадобилось сравнений символов