Алгоритм Манакера

Задача:

Пусть дана строка [math]s[/math]. Требуется найти все подстроки [math]s[/math], являющиеся палиндромами. Более формально, аса такие пары [math](i, j)[/math], что [math]s[i..j][/math] - палиндром (строка называется палиндромом, если она читается одинаково как слева направо, так и справа налево).

Уточнение постановки

Очевидно, что таких подстрок в худшем случае будет [math]n^2[/math]. Значит, нужно найти компактный способ хранения информации о них. Пусть [math]d1[i][/math] - длина максимального палиндрома нечетной длины с центром в позиции [math]i[/math], а [math]d2[i][/math] - аналогичная величина для палиндромов четной длины. Далее научимся вычислять значения этих массивов.

Наивный алгоритм

Идея

Опишем сначала наивный алгоритм решения задачи. Чтобы посчитать ответ для позиции [math]i[/math], будем на каждом шаге увеличивать длину палиндрома с центром в [math]i[/math] и убеждаться, что рассматриваемая строка не перестала быть палиндромом, либо не произошел выход за границы массива. Очевидно, что такой алгоритм будет работать за [math]O(n^2)[/math].

Псевдокод

 // [math]s[/math] — исходная строка
 // [math]d1, d2[/math] — массивы для записи ответа
 (int[], int[]) calculate(string s):
   for i = 1 to n
     d1[i] = 1
     while i - d1[i] > 0 and i + d1[i] <= n and s[i - d1[i]] == s[i + d1[i]]
       d1[i]++
     d2[i] = 0
     while i - d2[i] - 1 > 0 and i + d2[i] <= n and s[i - d2[i] - 1] == s[i + d2[i]]
       d2[i]++
     return (d1, d2)

Алгоритм Манакера

Идея

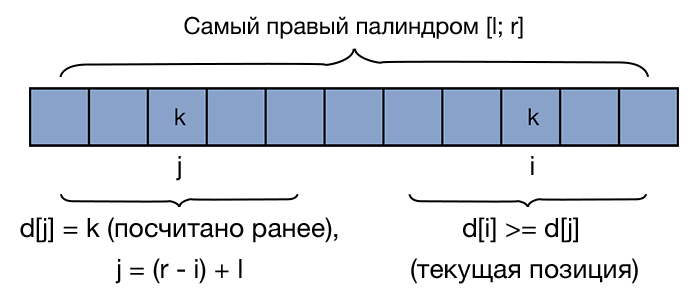
Алгоритм, который будет описан далее, отличается от наивного тем, что использует значения, посчитанные ранее. Будем поддерживать границы самого правого из найденных палиндромов — [math][l; r][/math]. Итак, пусть мы хотим вычислить [math]d1[i][/math] — т.е. длину наибольшего палиндрома с центром в позиции [math]i[/math]. При этом все предыдущие значения в массиве [math]d[/math] уже посчитаны. Возможны два случая:

1. [math]i \gt r[/math], т.е. текущая позиция не попадает в границы самого правого из найденных палиндромов. Тогда просто запустим наивный алгоритм для позиции [math]i[/math].
2. [math]i \leqslant r[/math]. Тогда попробуем воспользоваться значениями, посчитанным ранее. Отразим нашу текущую позицию внутри палиндрома [math][l;r] : j = (r - i) + l[/math]. Поскольку [math]i[/math] и [math]j[/math] — симметричные позиции, то мы можем утверждать, [math]d1[i] = d1[j][/math]. Однако надо не забыть про один граничный случай: что если [math]i + d1[j] - 1[/math] выходит за границы самого правого палиндрома? Так как информации о том, что происходит за границами это палинлрома у нас нет, то необходимо ограничить значение [math]d1[i][/math] следующим образом: [math]d1[i] = min(r - i, d1[j])[/math]. После этого запустим наивный алгоритм, который будет увеличивать значение [math]d1[i][/math], пока это возможно.

После каждого шага важно не забывать обновлять значения [math][l;r][/math].

Заметим, что массив [math]d2[/math] считается аналогичным образом, нужно лишь немного изменить индексы.

Псевдокод

Приведем код, который вычисляет значения массива [math]d1[/math]:

// [math]s[/math] — исходная строка
int l = 0
int r = -1
for i = 1 to n
  int k = 0
  if i <= r
     k = min(r - i, d[r - i + l])
  while i + k + 1 <= n and i - k - 1 > 0 and s[i + k + 1] == s[i - k - 1]
     k++
   d1[i] = k
   if i + k > r
     l = i - k
     r = i + k

Вычисление значений массива [math]d2[/math]:

// [math]s[/math] — исходная строка
int l = 0
int r = -1
for i = 1 to n
  int k = 0
  if i <= r
     k = min(r - i + 1, d[r - i + l + 1])
  while i + k <= n and i - k - 1 > 0 and s[i + k] == s[i - k - 1]
     k++
   d2[i] = k
   if i + k - 1 > r
     l = i - k
     r = i + k - 1

Оценка сложности

Внешний цикл в приведенном алгоритме выполняется ровно [math]n[/math] раз, где [math]n[/math] — длина строки. Попытаемся понять, сколько раз будет выполнен внутренний цикл, ответственный за наивный подсчет значений. Заметим, что каждая итерация вложенного цикла приводит к увеличению [math]r[/math] на [math]1[/math]. Действительно, возможны следующие случаи:

1. [math]i \gt r[/math], т.е. сразу будет запущен наивный алгоритм и каждая его итерация будет увеличивать значение [math]r[/math] хотя бы на [math]1[/math].
2. [math]i \leqslant r[/math]. Здесь опять два случая:
   1. [math]i + d[j] - 1 \leqslant r[/math], но тогда, очевидно, ни одной итерации вложенного цикла выполнено не будет.
   2. [math]i + d[j] - 1 \gt r[/math], тогда каждая итерация вложенного цикла приведет к увеличению [math]r[/math] хотя бы на [math]1[/math].

Т.к. значение [math]r[/math] не может увеличиваться более [math]n[/math] раз, то описанный выше алгоритм работает за линейное время.

См. также

• Префикс-функция
• Z — функция

Источники информации

• MAXimal :: algo :: Нахождение всех подпалиндромов
• Википедия — Поиск длиннейшей подстроки-палиндрома
• Алгоритмы для поиска палиндромов — Хабр