QpmtnriLmax

[math]Q \mid pmtn, r_i \mid L_{max}[/math]

Задача:

Рассмотрим задачу на нахождение расписания: У нас есть несколько станков, работающих параллельно. У станков могут быть разные скорости выполнения работ. Есть несколько заданий, каждое имеет своё время появления [math]r_i[/math] и время окончания [math]d_i[/math]. Работа может быть прервана в любой момент и продолжена позже на любой машине. Требуется минимизировать максимальное опоздание [math]L_{max} = \max\limits_i \{C_i - d_i\}[/math]

Алгоритм

Алгоритм решения

Рис. 2 - Расширение сети

Как в задаче [math]P \mid pmtn, r_i \mid L_{max}[/math] применим метод двоичного поиска и сведем задачу к [math] Q \mid pmtn, r_i, d_i \mid - [/math]. Для существования расписания с [math] L_{max} \le L^* [/math] требуется, чтобы у работы с номером [math] i [/math] выполнялось [math] C_i - d_i \le L^* [/math], что эквивалентно [math] C_i \le d_i + L^* [/math]. Опишем алгоритм решения [math] Q \mid pmtn, r_i, d_i \mid - [/math] при помощи сведения к задаче поиска максимального потока.

Пусть [math] t_1 \le t_2 \le ... \le t_r [/math] — упорядоченная последовательность всех значений [math]r_i[/math] и [math]d_i + L^*[/math]. Определим интервалы на исходной сети (Рис. 1) [math] I_K := [t_{K-1}, t_K], \ T_K = t_K-t_{K-−1} [/math] для [math] K = 2,..., r [/math]. Cчитаем, что станки занумерованы в порядке невозрастания скоростей [math] s_1 \ge s_2 \ge . . . \ge s_m [/math] (также считаем [math]s_{m+1} = 0[/math]).

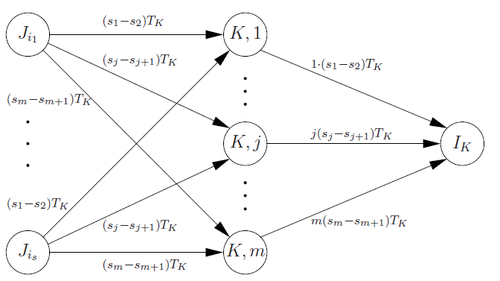
Искомая сеть строится с помощью расширения сети из задачи [math]P \mid pmtn, r_i \mid L_{max}[/math]. Обозначим через [math] J_{i_1}, J_{i_2}, . . . , J_{i_s} [/math] набор предшественников узла [math]I_K[/math], тогда замененная нами подсеть определяется как [math] I_K, J_{i_1}, J_{i_2}, . . . , J_{i_s} [/math].

Расширение сети показано на Рис. 2.

Расширенная подсеть строится путем добавления к вершинам [math] I_K, J_{i_1}, J_{i_2}, . . . , J_{i_s} [/math] вершин [math](K, 1), (K, 2), . . . (K, m) [/math]. При [math]j = 1,..., m [/math], есть дуги от [math](K, j)[/math] до [math]I_K[/math] с пропускной способностью [math] j(s_j - s_{j+1}) T_K [/math] и для всех [math]\nu = 1,. . . , s[/math] и [math]j = 1,. . ., m[/math] существует дуга из [math]J_{i_\nu}[/math] в [math](K, J)[/math] с пропускной способностью [math] (s_j - s_{j+1}) T_K [/math]. Это выполняется для каждой вершины [math]I_K[/math]. Кроме того, мы сохраняем дуги из [math]s[/math] в [math]J_i[/math] пропускной способностью [math]p_i[/math] и дуги из [math]I_K[/math] в [math]t[/math] пропускной способностью [math]S_mT_K[/math] (Рис. 1).

Теорема:

Следующие утверждения эквивалентны: [math](a)[/math] Существует допустимое расписание. [math](b)[/math] В расширенной сети существует поток от [math]s[/math] до [math]t[/math] со значением [math]\sum\limits_{i=1}^n p_i[/math]

Доказательство:

[math]\triangleright[/math]

[math](b) \Rightarrow (a):[/math] Рассмотрим в расширенной сети поток величиной [math]\sum\limits_{i = 1}^n {p_i}[/math]. Обозначим через [math]x_{iK}[/math] общий поток, который идет от [math]J_i[/math] до [math]I_K[/math]. Заметим, что [math]\sum\limits_{i = 1}^n \sum\limits_{K = 2}^r x_{iK} = \sum\limits_{i = 1}^n p_i[/math]. Достаточно показать, что для каждого подмножества [math]A \subseteq \{ 1, . . . , n \}[/math] выполняется [math]\sum\limits_{i \in A} x_{iK} \le T_Kh(A)[/math] ,где [math]h(A) = \begin{cases} S_{|A|}, & \text{if }|A| \le m \\ S_m, & \text{otherwise} \end{cases} [/math]. Это означает, что условие [math]\sum\limits_{i \in A} p_i \le Th(A), \forall A \subseteq \{ 1, ... , n \}[/math] выполняется и требования к обработке [math]x_{1K}, . . . , x_{nK}[/math] могут быть запланированы как [math]I_K[/math] для [math]K = 2, . . . , r[/math]. Рассмотрим подсеть в расширенной сети в подмножестве [math]A[/math] и соответствующие части потока. Фрагмент частичного потока, который проходит через [math](K, j)[/math] ограничен [math]\min \{ j(s_j −- s_{j + 1})T_K, |A|(s_j - s_{j+1})T_K \} = T_K(s_j - s_{j+1}) \min \{ j, |A| \}[/math]. Таким образом, мы имеем [math]\sum\limits_{i \in A} x_{iK} \ge T_K \sum\limits_{j = 1}^m(s_j −- s_{j+1}) \min \{ j, |A| \} = T_Kh(A)[/math]. [math](*)[/math] То, что равенство [math](*)[/math] справедливо, может рассматриваться как следствие. Если [math]|A| \gt m[/math], то [math]\sum\limits_{j = 1}^m \min \{ j, |A| \}(s_j - s_{j + 1}) = s_1 - s_2 + 2s_2 - 2s_3 + 3s_3 - 3s_4 + ... + ms_s - ms_{m+1} =\ [/math] [math]S_m = h(A)[/math]. В противном случае [math]\sum\limits_{j = 1} \min \{ j, |A| \}(s_j - s_{j + 1}) = s_1 - s_2 + 2s_2 - 2s_3 + 3s_3 - ... + (|A| - 1)s_{|A| - 1} -\ [/math] [math](|A| - 1)s_{|A|} + |A|(s_{|A|} - s_{|A| - 1} - ... - s_m + s_m - s_{m + 1}) = S_{|A|} = h(A)[/math]. [math](a) \Rightarrow (b):[/math] Предположим, что допустимое расписание существует. Для [math]i = 1, ... , n [/math] и [math]K = 2, ..., r[/math] пусть [math]x_{iK}[/math] является "объемом работ", который будет выполняться в интервале [math]I_K[/math] в соответствии с нашим возможным расписанием. Тогда для всех [math]K = 2, ..., r[/math] и произвольных наборов [math]A \subseteq \{ 1, . . . , n \}[/math], неравенство [math]\sum\limits_{i \in A} x_{iK} \le T_Kh(A)[/math] [math](**)[/math] выполняется. Кроме того, для [math]i = 1, . . . , n[/math] у нас [math]p_i = \sum\limits_{K = 2}^r s_{iK}[/math]. Остается показать, что можно отправить [math]x_{iK}[/math] от [math]J_i[/math] до [math]I_K[/math] [math](i = 1, . . . , n; K = 2, . . . , r)[/math] в расширенной сети. Такой поток существует, если [math]\forall A \subseteq \{ 1, . . . , n \}[/math] и [math]K = 2, . . . , r[/math] значение [math]\sum\limits_{i \in A} x_{iK}[/math] ограничено величиной минимального разреза части сети с истоками [math]J_i(i \in A)[/math] и стоком [math]I_K[/math]. Тем не менее, это значение [math]T_K\sum\limits_{j = 1}^m \min \{ j, |A| \}(s_j - s_{j+1})[/math] Используя [math](**)[/math] и правую часть [math](*)[/math], получаем [math]\sum\limits_{i \in A} x_{iK} \le T_K h(A) = T_K \sum\limits_{j = 1}^m \min \{ j, |A| \}(s_j - s_{j+1})[/math] что и является искомым неравенством.

[math]\triangleleft[/math]

Время работы

Работа с максимальным потоком в расширенной сети занимает [math]O (m n^3)[/math] шагов, проверка может быть сделана с такой же скоростью. Для решения [math]Q \mid pmtn; r_{i} \mid L_{max}[/math] мы используем бинарный поиск, а значит, получаем алгоритм с [math]\varepsilon[/math]-приближенной сложностью [math]O (mn^3(\log(n) + \log(1 / \varepsilon) + \log(\max\limits_{i=1}^{n} p_i)) [/math], потому как [math]L_{max}[/math], ограничен [math]n \max\limits_{i=1}^{n}p_i[/math], при [math]s_1 = 1[/math].

Задача [math]Q \mid pmtn; r_i \mid C_{max}[/math] представляет собой частный случай [math]Q \mid pmtn; r_i \mid L_{max}[/math], и может быть решена более эффективно. Лабетоль (Labetoulle J.), Лаулер (Lawler E.L.), Ленстра (Lenstra. J.K.), и Ринной Кан (Rinnooy Kan A.H.G.) разработали алгоритм работающий за [math] O(n \log(n) + mn) [/math] специально для этого случая.

Источники информации

• Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 379 стр. — ISBN 978-3-540-69515-8