Opij1di

[math] O \mid p_{i,j} = 1, d_i \mid - [/math]

Задача:

Дано [math]m[/math] одинаковых станков, которые работают параллельно, и [math]n[/math] работ, которые необходимо выполнить в произвольном порядке на всех станках. Любая работа на любом станке выполняется единицу времени. Для каждой работы есть время окончания [math]d_i[/math] — время, до которого она должна быть выполнена. Необходимо проверить, существует ли расписание, при котором все работы будут выполнены вовремя.

Описание алгоритма

Идея

Рис. 1. Работа [math]i[/math] назначена на интервалы [math]d_i - m + 1 \ldots d_i[/math].

Заметим, что если [math]d_i \lt m[/math], то очевидно, что [math]C_i \gt d_i[/math], следовательно, расписания не существует. Поэтому будем полагать, что [math]m \leqslant d_i[/math] для [math]i = 1 \ldots n[/math].

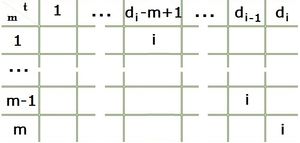
Определим [math]T = \max\limits_{i \in [1, n]}d_i[/math] — количество временных интервалов [math][t - 1, t][/math], где [math]t = 1 \ldots T[/math]. Будем обозначать [math][t - 1, t][/math] как [math]t[/math]. Для каждого из них мы можем назначить не более [math]m[/math] работ (по одной на каждый станок). Для каждой работы [math]i[/math] будем назначать времена обработки на каждой из машин следующим образом: на машине [math]m[/math] работа займет временной интервал [math]d_i[/math], на машине [math](m - 1)[/math] — интервал [math](d_i - 1)[/math] и так далее, на машине [math]1[/math] работа займет временной интервал [math]d_i - m + 1[/math]. В случае коллизий, то есть если найдется временной интервал [math]k \gt 1[/math], содержащий [math]m + 1[/math] работу, возьмем минимальный такой [math]k[/math] и перенесем лишнюю работу из него на ту же машину, но на один временной интервал левее. Будем повторять этот процесс, пока необходимо (и пока [math]k \gt 1[/math]). Таким образом, только первый временной интервал может содержать более [math]m[/math] работ. Причем это может произойти тогда и только тогда, когда задача не имеет решения, то есть не существует расписания, при котором все работы будут выполнены вовремя.

Псевдокод

Определим [math]h(t)[/math] — количество работ во временном интервале [math]t[/math].

void checkExistenceOfSchedule(int* [math]d[/math]):
  [math]T = \max\{d_i \mid i = 1 \ldots n\}[/math]
  for [math]t = 1[/math] to [math]T[/math]
     [math]h(t) = 0[/math]
  for [math]i = 1[/math] to [math]n[/math]
     for [math]j = d_i[/math] to [math]d_i - m + 1[/math]           (1)
        [math]h(j) = h(j) + 1[/math]
     while [math]\exists k \gt  1[/math] and [math]h(k) = m + 1[/math]     (2)
        find [math]\min\{k_0 \mid h(k_0) = m + 1\}[/math]
        [math]h(k_0 - 1) = h(k_0 - 1) + 1[/math]
        [math]h(k_0) = m[/math]
  if [math]h(1) \leqslant m[/math]
     return true
  else
     return false

Замечание: если расписание существует, то оно может быть вычислено данным алгоритмом, если добавить в цикл (1) функцию, отвечающую за добавление работы [math]i[/math] на момент [math]j[/math] в расписании для соответствующей машины и в цикл (2) функцию, отвечающую за перемещение работы, которой нет во временном интервале [math]k_0 - 1[/math], но которая есть в [math]k_0[/math], на момент [math]k_0 - 1[/math] в той же машине (этот шаг будет обоснован далее в доказательстве корректности).

Асимптотика

Покажем, что данный алгоритм может быть реализован за время [math]O(nm)[/math].
Для начала рассмотрим следующий вопрос: пусть [math]U[/math] — множество работ, для которого существует расписание, в котором отсутствуют опаздывающие работы, пусть [math]i[/math] — работа, не принадлежащая [math]U[/math], для которой выполняется неравенство [math]d_j \leqslant d_i[/math] для любой [math]j \in U[/math]. Можно ли построить расписание для множества [math]V = U \cup \{i\}[/math], в котором так же будут отсутствовать опаздывающие работы.
Введем несколько обозначений. Вектора [math]h[/math], соответствующие множествам [math]U[/math] и [math]V[/math] обозначим как [math]h^U[/math] и [math]h^V[/math] соответственно. [math]x(d_i)[/math] — количество временных интервалов [math]t[/math] со свойствами

• [math]d_i - m + 1 \leqslant t \leqslant d_i[/math],
• [math]h^U(t) \lt m[/math].

Будем говорить, что множество работ может быть выполнено вовремя, если существует расписание, в котором все работы из этого множества успевают выполниться без опозданий.

Лемма:

Пусть даны работы [math]1, 2 \ldots i[/math] с дедлайнами [math]d_1 \leqslant d_2 \leqslant \ldots \leqslant d_i[/math], [math]U = \{1, 2, \ldots i - 1\}[/math] и [math]V = U \cup \{i\}[/math]. Тогда для всех работ [math]j = d_i - m + 1 \ldots d_i[/math], для которых [math]h^U(j) \lt m[/math], будет верно, что [math]h^V(j) = h^U(j) + 1[/math].

Доказательство:

[math]\triangleright[/math]

Рассмотрим вектора [math]h^U[/math] и [math]h^V[/math] после [math]i - 1[/math] и [math]i[/math] итераций алгоритма. Заметим, что значения вектора [math]h[/math], не превосходящие [math]m[/math], то есть [math]h(j) \lt m[/math], никогда не уменьшаются. Следовательно, если [math]d_i - m + 1 \leqslant j \leqslant d_i[/math] и [math]h^U(j) \lt m[/math], то [math]h^V(j) \geqslant h^U(j) + 1[/math]. Чтобы показать, что ситуация, когда при тех же условиях [math]h^V(j) \geqslant h^U(j) + 2[/math], невозможна, рассмотрим расписание, построенное алгоритмом. Если [math]h^V(j) \geqslant h^U(j) + 2[/math], то это значит, что в течение [math]i[/math] итерации во временной интервал [math]j[/math] была добавлена работа [math]i[/math] и еще как минимум одна работа, пусть работа [math]k[/math], была перемещена из временного интервала [math]j + 1[/math] в [math]j[/math]. Это возможно только если работа [math]k[/math] ни на одной машине не была назначена до временного интервала [math]j[/math]. Следовательно, работа [math]k[/math] выполняется во временной интервал [math]j[/math] и некоторые временные интервалы [math]v \gt j + 1[/math], откуда следует, что [math]j \lt d_k - m + 1 \leqslant d_i - m + 1[/math], что приводит нас к противоречию.

[math]\triangleleft[/math]

Теорема:

Пусть [math]U[/math] — множество работ, которое может быть выполнено вовремя, пусть [math]i[/math] — работа, не принадлежащая [math]U[/math], для которой выполняется неравенство [math]d_j \leqslant d_i[/math] для любой [math]j \in U[/math]. Тогда множество работ [math]V = U \cup \{i\}[/math] может быть выполнено вовремя тогда и только тогда, когда [math]x(d_i) + \sum\limits_{t = 1}^{d_i - m}(m - h^U(t)) \geqslant m[/math] (1).

Доказательство:

[math]\triangleright[/math]

Неравенство (1) равносильно [math](d_i - m)m \geqslant \sum\limits_{t = 1}^{d_i - m}h^U(t) + m - x(d_i)[/math]. По лемме имеем [math]\sum\limits_{j = d_i - m + 1}^{d_i}h^V(j) = \sum\limits_{j = d_i - m + 1}^{d_i}h^U(j) + x(d_i)[/math]. Вычитая это равенство из [math]\sum\limits_{j = 1}^{d_i}h^V(j) = \sum\limits_{j = 1}^{d_i}h^U(j) + m[/math], получим [math]\sum\limits_{t = 1}^{d_i - m}h^V(t) = m - x(d_i) + \sum\limits_{t = 1}^{d_i - m}h^U(t)[/math]. Следовательно, мы пришли к тому, что (1) равносильно [math](d_i - m)m \geqslant \sum\limits_{t = 1}^{d_i - m}h^U(t)[/math]. Обозначим [math]T = d_i - m[/math], тогда предыдущее равенство превращается в [math]Tm \geqslant \sum\limits_{t = 1}^{T}h^U(t)[/math] (2). Остается показать, что если равенство (2) выполняется для [math]T = d_i - m[/math], тогда оно выполняется и для [math]T = 1, \ldots d_i - m - 1[/math]. Докажем индукцией по [math]T[/math], что равенство (2) выполняется для [math]T = 1, \ldots d_i - m[/math], взяв как базу [math]T = d_i - m[/math]. База. По теореме из доказательства корректности [math]h^V(1) \leqslant m[/math] означает, что [math]V[/math] может быть выполнено вовремя. С другой стороны, если [math]h^V(1) \leqslant m[/math], то выполняется (2), так как [math]h^V(t) \leqslant m[/math] для всех [math]t \geqslant 2[/math] по построению [math]h^V[/math]. Переход. Предположим, что (2) выполняется для некоторого [math]T \in (1, d_i - m][/math]. Покажем, что тогда неравенство выполняется и для [math]T - 1[/math]. Рассмотрим два случая в зависимости от значения [math]h^V(T)[/math]: [math](a)[/math] Пусть [math]h^V(T) = m[/math]. Так как равенство (2) выполняется для [math]T[/math], то верно [math](T - 1)m \geqslant \sum\limits_{t = 1}^{T}h^V(t) - m = \sum\limits_{t = 1}^{T - 1}h^V(t)[/math]. Следовательно, (2) выполняется и для [math]T - 1[/math]. [math](b)[/math] Пусть [math]h^V(T) \lt m[/math]. В расписании для множества работ [math]V[/math] все стадии обработки работы [math]i[/math] ([math]k[/math] стадия обработки — выполнение работы на [math]k[/math] машине) должны быть назначены на временные интервалы из отрезка [math][T - 1, d_i][/math], так как [math]T \leqslant d_i - m[/math] и в период времени [math][T - 1, T][/math] есть свободная машина. Все стадии обработки работ в расписании для [math]U[/math], назначенные на временные интервалы из отрезка [math][T - 1, d_i][/math], в расписании для [math]V[/math] назначены на временные интервалы из того же отрезка [math][T - 1, d_i][/math]. И так как [math]U[/math] по условию может быть выполнено вовремя, верно неравенство [math](T - 1)m \geqslant \sum\limits_{t = 1}^{T - 1}h^U(t) = \sum\limits_{t = 1}^{T - 1}h^V(t)[/math]. Следовательно, (2) выполняется и для [math]T - 1[/math].

[math]\triangleleft[/math]

Пусть [math]k = |U|[/math] — мощность множества [math]U[/math]. Тогда [math]\sum\limits_{j = 1}^{d_i - m}(m - h^U(j)) = m(d_i - m) - \sum\limits_{j = 1}^{d_i - m}h^U(j) = m(d_i - m) - (km - \sum\limits_{j = d_i - m + 1}^{d_i}h^U(j))[/math]. Таким образом, (1) равносильно [math]m(d_i - m) - (km - \sum\limits_{j = 1}^{m}h^U(d_i - m + j)) + x(d_i) \geqslant m[/math] (3). Мы пришли к тому, что нам достаточно знать только значения [math]h^U(d_i - m + 1) \ldots h^U(d_i)[/math] и мощность [math]k[/math] множества [math]U[/math], чтобы проверить, выполняется ли (3), то есть может ли множество [math]V = U \cup \{i\}[/math] быть выполнено вовремя. Очевидно, что (3) может быть вычислено за время [math]O(m)[/math].

Доказательство корректности

Теорема:

Для множества работ с дедлайнами [math]d_1, d_2, \ldots d_n[/math] задача имеет решение тогда и только тогда, когда [math]h(1) \leqslant m[/math].

Доказательство:

[math]\triangleright[/math]

[math]\Rightarrow[/math] Если задача имеет решение, то очевидно, что первый временной интервал не может быть переполнен. [math]\Leftarrow[/math] Изначально алгоритм присваивает все стадии обработки каждой работы [math]i[/math] (то есть обработку на каждом станке) попарно различным временным интервалам. Если [math]\exists k \gt 1 : h(k) = m + 1[/math] и [math]h(k - 1) \leqslant m[/math], то это значит, что существует как минимум одна работа, которая назначена временному интервалу [math]k[/math], но которой нет во временном интервале [math]k - 1[/math]. Следовательно, после перемещения вектор [math]h[/math] по-прежнему будет удовлетворять условию, что каждая работа принадлежит [math]m[/math] разным временным интервалам, причем в каждом из них она будет выполняться на разных машинах, так как при перемещении работ машины остаются прежними. Таким образом, если [math]h(1) \leqslant m[/math], то [math]h(t) \leqslant m[/math], где [math]t = 1 \ldots T[/math], то есть существует решение, при котором все работы будут выполнены вовремя.

[math]\triangleleft[/math]

См. также

• [math]O \mid p_{ij} = 1 \mid \sum U_i[/math]
• [math]O2 \mid \mid C_{max}[/math]

Источники информации

• Peter Brucker «Scheduling Algorithms», fifth edition, Springer — с. 163-168 ISBN 978-3-540-69515-8