Алгоритм Ахо-Корасик

Задача:

Дан набор строк в алфавите размера [math]k[/math] суммарной длины [math]m[/math]. Найти для каждой строки все ее вхождения в текст за время [math]O(m)[/math] и [math]O(mk)[/math] памяти.

Алгоритм

Шаг 1. Построение бора

Строим бор из строк.
Построение выполняется за время [math]O(m)[/math], где [math]m[/math] — суммарная длина строк.

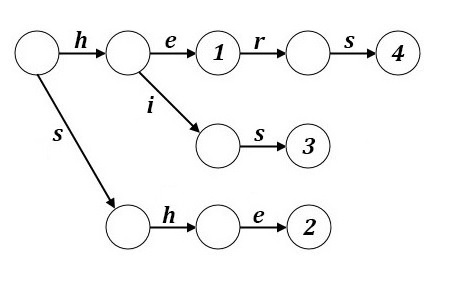
Пример построенного бора

Бор для набора строк [math] \{ \textbf{he}, \textbf{she}, \textbf{his}, \textbf{hers}\} [/math]:

Шаг 2. Преобразование бора.

Обозначения: [math][u][/math] — слово, приводящее в вершину [math]u[/math] в боре.
Узлы бора можно понимать как состояния автомата, а корень как начальное состояние.
Узлы бора, в которых заканчиваются строк, становятся терминалами.
Для переходов по автомату заведём в узлах несколько функций:

• [math]\mathrm{parent}(u)[/math] — возвращает родителя вершины [math]u[/math];
  
• [math]\pi(u) = \delta(\pi(\mathrm{parent}(u)), c)[/math] — суффиксная ссылка; здесь [math]u[/math] — сын [math]\mathrm{parent}(u)[/math] по символу [math]c[/math];
  
• [math]\delta(u, c) = \begin{cases} v, &\text{if $v$ is son by symbol $c$ in trie;}\\ root, &\text{if $u$ is root and $u$ has no child by symbol $c$ in trie}\\ \delta(\pi(u), c), &\text{else.} \end{cases}[/math] — функция перехода.

Суффиксная ссылка [math]\pi(u) = v[/math], если [math][v][/math] — максимальный суффикс [math][u][/math], [math][v]\neq[u][/math]. Функции перехода и суффиксные ссылки можно найти либо алгоритмом обхода в глубину с ленивыми вычислениями, либо с помощью алгоритма обхода в ширину.

Пример автомата Ахо-Корасик

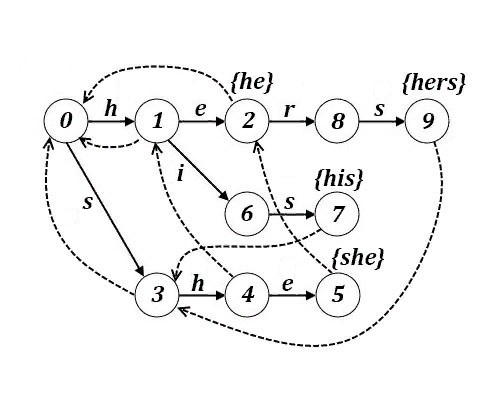
Пунктиром обозначены суффиксные ссылки. Из вершин, для которых они не показаны, суффиксные ссылки идут в корень.

Шаг 3. Построение сжатых суффиксных ссылок.

[math]up(u) = \begin{cases} \pi(u), &\text{if $\pi(u)$ is terminal;}\\ \varnothing,&\text{if $\pi(u)$ is root;}\\ up(\pi(u)), &\text{else.} \end{cases}[/math] — сжатая суффиксная ссылка, т.е. ближайшее допускающее состояние (терминал) перехода по суффиксным ссылкам.

Сжатые суффиксные ссылки могут отыскиваться при помощи ленивой рекурсии.

Использование автомата

По очереди просматриваем символы текста. Для очередного символа [math]c[/math] переходим из текущего состояния [math]u[/math] в состояние, которое вернёт функция [math]\delta(u, c)[/math]. Оказавшись в новом состоянии, отмечаем по сжатым суффиксным ссылкам строки, которые нам встретились и их позицию (если требуется). Если новое состояние является терминалом, то соответствующие ему строки тоже отмечаем.
Примечание. Если требуется найти только первое вхождение строки в текст, то существенно ускорить работу алгоритма могут пометки о посещённости узла, т.е. если узел посещён, то не переходить по сжатым суффиксным ссылкам. Вместо хранения пометок можно просто сбрасывать сжатую суффиксную ссылку.

Пример реализации

Ниже представлена реализация некоторых функций (используется ленивая рекурсия).

Структура вершины:

struct Node:
    Node son[k]        // массив сыновей; k - это размер алфавита
    Node go[k]         // массив переходов (запоминаем переходы в ленивой рекурсии)
    Node parent         // вершина родитель
    Node suffLink       // суффиксная ссылка (вычисляем в ленивой рекурсии)
    Node up             // сжатая суффиксная ссылка
    char charToParent    // символ, ведущий к родителю
    bool isLeaf            // флаг, является ли вершина терминалом
    vector<int> leafPatternNumber   // номера строк, за которые отвечает терминал

Функция, для вычисления суффиксной ссылки:

Node getSuffLink(Node v):
    if not v.suffLink  // если суффиксная ссылка ещё не вычислена
       if v == root or v.parent == root
            v.suffLink = root
          else
            v.suffLink = getLink(getSuffLink(v.parent), v.charToParent)
    return v.suffLink

Функция, для вычисления перехода:

Node getLink(Node v, char c): 
   if not v.go[c]   // если переход по символу c ещё не вычислен
        if v.son[c]
            v.go[c] = v.son[c]
         else if v == root 
            v.go[c] = root 
         else 
            v.go[c] = getLink(getSuffLink(v), c)
    return v.go[c]

Функция, для вычисления сжатой суффиксной ссылки:

Node getUp(Node v):
    if not v.up      // если сжатая суффиксная ссылка ещё не вычислена
        if getSuffLink(v).isLeaf
            v.up = getSuffLink(v)
          else if getSuffLink(v) == root
            v.up = root
          else 
            v.up = getUp(getSuffLink(v))
    return v.up

Функция, для добавление строки в бор:

fun addString(string const& s, int patternNumber):
    Node cur = root
    for i = 0 to s.length - 1
        char c = s[i] - 'a'
        if cur.son[c] == 0
            cur.son[c] = Node
            /* здесь также нужно обнулить указатели на переходы и сыновей */
            cur.son[c].suffLink = 0
            cur.son[c].up = 0
            cur.son[c].parent = cur
            cur.son[c].charToParent = c
            cur.son[c].isLeaf = false
        cur = cur.son[c]
    cur.isLeaf = true
    cur.leafPatternNumber.push_back(patternNumber)

Функция, для процессинга текста (поиск, встречается строка или нет):

fun processText(string const& t, vector<bool>& found):   // found - это вектор, длина которого равна количеству строк
    found.assign(w, false)   // w - количество строк
    Node cur = root
    for i = 0 to t.length - 1 
        char c = t[i] - 'a'
        cur = getLink(cur, c)
        for j = 0 to cur.leafPatternNumber.size - 1
            found[cur.leafPatternNumber[j]] = true
        /* В этом месте кода должен выполняться переход по сжатой суффиксной ссылке getUp(cur). Для вершины,
           обнаруженной по ней тоже ставим, что она найдена, затем повторяем для её сжатой суффиксной ссылки
           и так до корня. Хорошо ускорит программу сброс сжатых суффиксных ссылок для посещённых вершин. */

Кроме этих функций требуется инициализация, но она имеет отношение только к кодированию, поэтому здесь приведена не будет.

Поиск шаблонов с масками

Задача:

Пусть [math]\varphi[/math] — маска, обозначающая любой одиночный символ. Необходимо найти для каждого заданного шаблона с масками все его вхождения в текст.

Например, шаблон [math]ab\varphi\varphi c\varphi[/math], который содержит в себе три маски, встречается на позициях [math]2[/math] и [math]8[/math] строки [math]xabvccababcax[/math].

Алгоритм поиска

Для того чтобы найти все вхождения в текст заданного шаблона с масками [math]Q[/math], необходимо обнаружить вхождения в текст всех его безмасочных кусков.
Пусть [math]\{Q_1, \dots, Q_k \}[/math] — набор подстрок [math]Q[/math], разделенных масками, и пусть [math]\{ l_1, \dots, l_k \}[/math] — их стартовые позиции в [math]Q[/math]. Например, шаблон [math]ab\varphi\varphi c\varphi[/math] содержит две подстроки без масок [math]ab[/math] и [math]c[/math] и их стартовые позиции соответственно [math]1[/math] и [math]5[/math]. Для алгоритма понадобится массив [math]C[/math]. [math]C[i][/math] — количество встретившихся в тексте безмасочных подстрок шаблона, который начинается в тексте на позиции [math]i[/math]. Тогда появление подстроки [math]Q_i[/math] в тексте на позиции [math]j[/math] будет означать возможное появление шаблона на позиции [math]j - l_i + 1[/math].

1. Используя алгоритм Ахо-Корасик, находим безмасочные подстроки шаблона [math]Q[/math]: когда находим [math]Q_i[/math] в тексте [math]T[/math] на позиции [math]j[/math], увеличиваем на единицу [math]C[j - l_i + 1][/math].
   
2. Каждое [math]i[/math], для которого [math]C[i] = k[/math], является стартовой позицией появления шаблона [math]Q[/math] в тексте.
   

Рассмотрим подстроку текста [math]T[i \dots i+n-1][/math]. Равенство [math]C[i] = k[/math] будет означать, что подстроки текста [math] T[i + l_1 \dots i + l_1 + |Q_1| - 1], T[i + l_2 \dots i + l_2 + |Q_2| - 1][/math] и так далее будут равны соответственно безмасочным подстрокам шаблона [math]\{Q_1, \dots , Q_k \}[/math]. Остальная часть шаблона является масками, поэтому шаблон входит в текст на позиции [math]i[/math].
Поиск подстрок заданного шаблона с помощью алгоритма Ахо-Корасик выполняется за время [math]O(m+n+a)[/math], где [math]n[/math] — суммарная длина подстрок, то есть длина шаблона, [math]m[/math] — длина текста, [math]a[/math] — количество появлений подстрок шаблона. Далее просто надо пробежаться по массиву [math]C[/math] и просмотреть значения ячеек за время [math]O (m)[/math].

См. также

• Алгоритм Бойера-Мура
• Алгоритм Кнута-Морриса-Пратта

Источники информации

• MAXimal :: algo :: Алгоритм Ахо-Корасик
• Сопоставление множеств и алгоритм Ахо-Корасик
• Codeforces :: Алгоритм Ахо-Корасик
• Habr :: Алгоритм Ахо-Корасик
• Wiki :: Алгоритм Ахо-Корасик