Pintreepi1Lmax

[math]P \mid intree, p_{i} = 1 \mid L_{max}[/math]

Задача:

Рассмотрим задачу на нахождение расписания: У нас есть несколько станков, работающих параллельно. У станков могут быть разные скорости выполнения работ. Есть несколько заданий, каждое из которых имеет определенный порядок, который указан в направленном из корней в лист intree-дерева, которое имеет несколько корней и один лист. Любая работа на любом станке выполняется единицу времени. Требуется минимизировать максимальное опоздание [math]L_{max} = \max\limits_i \{C_i - d_i\}[/math].

Описание алгоритма

Пример intree-дерева

Идея

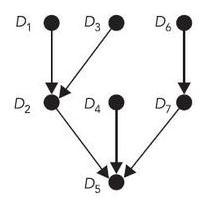
Все работы хранятся в качестве вершин intree-дерева, состоящем из [math]n[/math] вершин. В intree-дереве у одной вершины может быть два и более родителей. Решение задачи состоит из двух шагов:

1. Меняем делайны работ в соответствии с их очередностью: для всех [math]i, j[/math] таких, что существует ребро из [math]i[/math] в [math]j[/math] будем менять [math]{d_i}[/math] на [math]\min ({d_i}, {d_j} - 1) [/math].
2. Работы расставляются в неубывающем порядке их дедлайнов.

Псевдокод

Первый шаг

Алгоритм изменения сроков:

В массиве [math]\mathtt j[/math] хранятся работы, имеющие поле [math]\mathtt d[/math] — дедлайн.

int i = 0
deque = [math]\varnothing[/math]
for int k = 1 .. n  // ищем лист в дереве, из него будет производиться обход дерева  
   if j[k].parents == [math]\varnothing[/math]
       i = k    // такая вершина только одна (intree-дерево из условия)  
deque.push(i)
while not deque.isEmpty
    i = deque.removeFirst()
    for int k in j[i].parents
        j[k].d = min(j[k].d, j[i].d - 1)
        deque.addLast(k)

Второй шаг

На втором этапе алгоритма работы сортируются в неубывающем порядке их дедлайнов. Предполагается, что работы будут занумерованы так, что [math]d_{i} \leqslant d_{j}[/math], если [math]i \leqslant j[/math].

• В переменной [math]\mathtt F[/math] хранится время, когда какой-либо станок освободится.
• В массиве [math]\mathtt r[/math] хранится информация о максимальном времени завершении обработки родителя.
• Массив [math]\mathtt q[/math] хранит информацию о количестве работ, готовых к исполнению (находящихся в очереди) в момент времени [math]t[/math].
• Массив [math]\mathtt x[/math] хранит информацию о начале выполнения работы [math]i[/math].

F = 0
for int i = 1 .. n
   r[i] = 0
for int t = 0 .. n
   q[t] = 0
for int i = 1 .. n
   int t = max(r[i], F)
   x[i] = t
   q[t] = q[t] + 1
   if q[t] == m
      F = t + 1
   j = i.child()
   r[j] = max(r[j], t + 1)

В результате ответ можно получить, зная конечный массив [math]\mathtt x[/math] и делайны работ: [math]L_{max} = \max\limits_i \{\mathtt x[i] - \mathtt j[i].d\}[/math], где [math] \mathtt j[/math] — массив работ, описанный в первом пункте. Можно заметить, что при вычислении ответа неважно, какие дедлайны использовать, начальные или релаксированные, потому что для любого [math]k[/math] и его предка [math]i[/math] выполняется неравенство [math] \mathtt j[k].d \leqslant \mathtt j[i].d - 1[/math], а значит, после релаксации минимум не изменится. (При условии, что существует правильное расписание)

Доказательство корректности

Первый шаг

Лемма:

Работа с новым сроком [math]{d'_i}[/math] в расписании не имеет опозданий тогда и только тогда, когда она не имела опозданий с оригинальным сроком [math]{d_i}[/math].

Доказательство:

[math]\triangleright[/math]

[math]\Rightarrow [/math] Т.к. [math]{d'_i} \leqslant {d_i}[/math], значит, если опозданий не было со значениями [math]{d'_i}[/math], их не будет и со значениями [math]{d_i}[/math]. [math]\Leftarrow [/math] Пусть у нас были сроки [math]{d_i}[/math] и мы их заменили на [math]{d'_i}[/math] в соответствии с приведенным алгоритмом. Пронумеруем вершины от [math]1[/math] до [math]n[/math] в соответствии с обратным порядком обхода в алгоритме изменения сроков, причём [math]d_{i} \leqslant d_{j}[/math], если [math]i \leqslant j[/math]. В соответствии с расписанием, время, когда деталь закончит обрабатываться на станке [math]{C_i}[/math] удовлетворяет неравенству [math]{C_i} \leqslant {d_i}[/math] для всех [math]{C_1} \dots {C_n}[/math]. Тогда мы имеем [math]{C_n} \leqslant {d_n} = {d'_n}[/math]. Если для какого-то [math]1 \lt r \leqslant n[/math] мы имеем [math]{C_n} \leqslant {d'_n}[/math] для [math]i = r \dots n [/math] и существует работа [math]j[/math] из этого промежутка, что вершина с номером [math]r - 1[/math] является ее родителем, тогда [math]C_{r-1} \leqslant \min(d_{r-1},d'_{j}-1) = d'_{r-1}[/math].

[math]\triangleleft[/math]

Второй шаг

Расписание, сгенерированное этим алгоритмом имеет важное свойство: число заданий в очереди в любой момент времени [math]t[/math] меньше, чем в момент [math]t + 1[/math]. Действительно, пусть во время [math]t[/math] мы выполняем [math]k[/math] работ, и хотя бы [math]k + 1 \leqslant m[/math] работ готовы к выполению в момент времени [math]t + 1[/math]. Но т.к. [math]k + 1 \leqslant m[/math], значит каждой из работ предшествовала как минимум одна, поскольку у всех вершин, кроме корней, есть как минимум один предок. Значит, в момент времени [math]t[/math] исполнялось не менее [math]k + 1[/math] работ, противоречие.

Лемма:

Если существует такое расписание, в котором ни одна из работ не будет выполнена с опозданием, то тогда это свойство сохранится в построенном данным алгоритмом расписании

Доказательство:

[math]\triangleright[/math]

Предположим, что существует работа из [math]x_{1} \dots x_{n}[/math] расписания, построенного алгоритмом. В таком случае существует работа, которая опоздала по отношению к измененным срокам. Возьмем наименьшее [math]i[/math] такое, что [math]x(i) + 1 \gt d'_{i}[/math]. Пусть [math]t \lt d'_{i}[/math] — наибольшее из удовлетворяющих условию [math]j \lt m [/math], где [math] x(j) = t, d'_{j} \leqslant d'_{i}[/math] Такое [math]t[/math] существует, потому что иначе [math]m \cdot d'_{i}[/math] работ [math]j[/math] с [math]d'_{j} \leqslant d'_{i}[/math] находятся в очереди до [math]d'_{i}[/math]. Работа [math]i[/math] к ним не принадлежит, поскольку [math]x(i) + 1 \gt d'_{i}[/math], а значит, что [math]m \cdot d'_{i} + 1[/math] должны быть в очереди в момент времени [math]0 \dots d'_{i}[/math] и ни одна работа не должна опаздывать. Противоречие. Любая работа [math]j[/math] с [math]d'_{j} \leqslant d'_{i} [/math] и [math] x(j) \gt t [/math] должна иметь предка, начавшего работать в момент времени [math]t[/math]. Теперь рассмотрим два случая: Первый случай: [math]t = d'_{i} - 1[/math]. Мы имеем [math]x(i)\gt d'_{i}-1 = t[/math]. Таким образом, предок [math]k[/math] работы [math]i[/math] должен начать работать во время [math]t[/math] и закончить в [math]d'_{i}[/math]. Но т.к. [math]d'_{k} \leqslant d'_{i} - 1 \lt d'_{i} = x(k) + 1[/math], работа [math]k[/math] так же опоздает, однако [math]i[/math] было выбрано минимальным. Противоречие. Второй случай: [math]t \lt d'_{i} - 1[/math]. В этом случае [math]m[/math] работ [math]j[/math] таких, что [math]d'_{j} \leqslant d'_{i}[/math] начнут работать в момент времени [math]t + 1[/math], каждая из которых имеет как минимум работающего в [math]t[/math] предка. По структуре дерева все эти предки различны, кроме того, если [math]k[/math] — такой предок [math]j[/math], тогда [math]d'_{k} \leqslant d'_{j} - 1 \lt d'_{j} \leqslant d'_{i}[/math], что противоречит выбору [math]t[/math]

[math]\triangleleft[/math]

Корректность алгоритма

Теорема:

Данный алгоритм корректно решает задачу [math]P \mid intree, p_{i} = 1 \mid L_{max}[/math]

Доказательство:

[math]\triangleright[/math]

Пусть [math]L'_{max}[/math] — оптимальное значение. В таком случае, существует расписание, удовлетворяющее [math]\max\limits_i \{C_i - d_i\} \leqslant L'_{max}[/math], что эквивалетно выражению [math]C_{i} \leqslant d_{i} + L'_{max}[/math] для [math]i = 1 \dots n [/math]. По первой лемме расписание [math]S[/math], построенное для сдвинутых дат [math]d_{i} + L'_{max}[/math] удовлетворяет данным выражениям. Таким образом, оно оптимально. Нетрудно заметить, что [math]S[/math] идентично расписанию, построенному алгоритмом, т.к. [math](d_{i}+L'_{max})' = d'_{i} + L'_{max} [/math] для [math]i = 1 \dots n [/math]

[math]\triangleleft[/math]

Асимптотика

1. На первом шаге мы посещаем каждую вершину не более двух раз (первый — когда ищем вершину без родителя, второй — когда релаксируем дедлайны) за [math]O(n)[/math] времени.
2. Делаем сортировку вершин за [math]O(n \log n)[/math], а затем обходим все вершины по разу и считаем время начала выполнения каждой работы, в сумме за [math]O(n)[/math].

Итоговая сложность — [math]O(n \log n)[/math]

См. также

• [math]P2 \mid prec, p_i = 1 \mid L_{\max}[/math]
• [math]1 \mid outtree \mid \sum w_i C_i[/math]

Источники информации

• Peter Brucker «Scheduling Algorithms», fifth edition, Springer — с. 151-156 ISBN 978-3-540-69515-8