Фундаментальные циклы графа — различия между версиями
| Строка 1: | Строка 1: | ||
{{Определение | {{Определение | ||
|definition= | |definition= | ||
| − | '''Фундаментальный цикл графа <tex>G</tex> относительно остова <tex>T</tex>''' {{---}} простой цикл <tex>C</tex>, полученный путем добавления добавления к [[Остовные деревья: определения, лемма о безопасном ребре|остову]] <tex>T</tex> ребра <tex>e_1e_2 \notin T.</tex>}} | + | '''Фундаментальный цикл графа <tex>G</tex> относительно остова <tex>T</tex>''' ('' англ. fundamental cycle'') {{---}} простой цикл <tex>C</tex>, полученный путем добавления добавления к [[Остовные деревья: определения, лемма о безопасном ребре|остову]] <tex>T</tex> ребра <tex>e_1e_2 \notin T.</tex>}} |
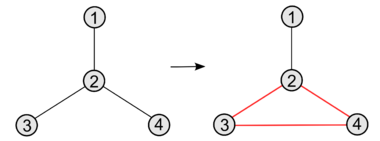
[[Файл:Fundomential.png|380px|центр|thumb|Пример фундаментального цикла в графе. <font color=#ED1C24>Красным</font> выделен фундаментальный цикл, полученный добавлением ребра <tex>(3, 4)</tex>]] | [[Файл:Fundomential.png|380px|центр|thumb|Пример фундаментального цикла в графе. <font color=#ED1C24>Красным</font> выделен фундаментальный цикл, полученный добавлением ребра <tex>(3, 4)</tex>]] | ||
Версия 22:10, 20 октября 2016
| Определение: |
| Фундаментальный цикл графа относительно остова ( англ. fundamental cycle) — простой цикл , полученный путем добавления добавления к остову ребра |
| Теорема: |
Множество всех фундаментальных циклов относительно любого остова графа образует базис циклического пространства этого графа. |
| Доказательство: |
|
Рассмотрим остов графа и фундаментальные циклы относительно остова . В каждом цикле есть ребро , которое принадлежит ровно одному из . Поэтому сумма различных фундаментальных циклов относительно остова не является пустым графом, из чего следует, что линейно независимы. Докажем, что любой цикл из циклического пространства графа является суммой фундаментальных циклов. Пусть — цикл циклического пространства графа , ребра принадлежащие и не принадлежащие . Рассмотрим граф . Каждое из ребер встречается ровно в двух слагаемых — и . Значит содержит только ребра из . Так как простые циклы, то степени всех их вершин четны, степени вершин тоже четны по лемме, значит степени всех вершин четны. Если непустой граф, то в есть цикл, значит цикл есть и в . Значит пустой граф, откуда следует что . |
См. также
Источники информации
- Харари Фрэнк Теория графов = Graph theory/Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6