Гиперграфы

Гиперграфом (англ. hypergraph) называется обобщение графа, в котором каждое ребро соединяет необязательно две вершины. Формально, гиперграф — упорядоченная пара [math]H = (V,E)[/math], где [math]V[/math] — множество вершин гиперграфа, а [math]E[/math] — множество ребер гиперграфа, где каждое ребро является подмножеством множества вершин.

В дальнейшем будем считать, что все рассматриваемые гипергафы обладают свойствами:

• [math]\forall i[/math] [math] E_i \neq \emptyset [/math]

• [math] \cup E = X [/math]

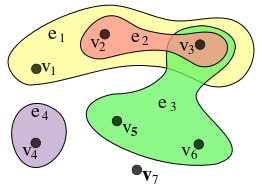
Частный случай гипергафа, где [math]E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}[/math]

Стоит заметить, что обычный граф является частным случаем гиперграфа, где каждое ребро имеет мощность [math]2[/math].

Определения

Подгиперграфом (англ. subhypergraph) [math]H_1[/math] гиперграфа [math]H=(V,E)[/math] назывется гипергаф: [math]H_1 = (V_1, \{E_1 | \forall i: e_i \cap V_1 \neq \emptyset \})[/math]. Иначе, подгипергаф — это гипергаф с некоторомы удаленными вершинами.

Реберным гиперграфом (англ. dual) [math]H^* = L(H)[/math] называется гипергаф: [math]H^* = (V^*, E^*) = (E, V) = (\{e_1, e_2 \ldots\},\{v_1,v_2\ldots\}) = (\{v^*_1, v^*_2 \ldots\},\{e^*_1, e^*_2\ldots\})[/math], где вершина [math]v^*_i[/math] принадлежит ребру [math]e^*_j[/math], если вершина [math]v_j[/math] принадлежит ребру [math]e_i[/math] в исходном гиперграфе [math]H[/math]. Оче

Ацикличность

Заметим, что гиперграф удобно задавать матрицей инцидентности.