Convex hull trick

Note Bene

      Convex hull - выпуклая оболочка по-английски

      Convex hull trick - один из методов оптимизации динамического программирования

      Техника впервые появилась в 1995 году (задачу на нее предложили в USACO - национальной олимпиаде США по программированию). 
      Массовую известность получила после IOI (международной олимпиады по программированию для школьников) 2002

Постановка примера задачи

Рассмотрим типичную задачу на ДП:

      Есть n деревьев с высотами [math]a1, a2, \dots an[/math] (в метрах). Требуется спилить их все, потратив минимальное количество монет на заправку
      бензопилы. Но пила устроена так, что она может спиливать только по 1 метру от дерева, к которому ее применили. Также после
      срубленного метра (любого дерева) пилу нужно заправлять, платя за  бензин определенной кол-во монет. Причем стоимость 
      бензина зависит от срубленных (полностью) деревьев. Если сейчас максимальный индекс срубленного дерева равен i, то цена заправки 
      равна ci.  Изначально пила заправлена.
      Также известны следующие ограничения : [math]c[n] = 0, a[1] = 1, a[i][/math] возрастают, [math]c[i][/math] убывают.
      (убывание и возрастание нестрогие)

(Задача H отсюда : http://neerc.ifmo.ru/school/camp-2016/problems/20160318a.pdf)

Наивное решение

Перед началом решения заметим важный факт, напрямую следующий из условия : т.к. c[i] убывают(нестрого) и c[n] = 0, то все c[i] не отрицательны.

Понятно, что нужно затратив минимальную стоимость срубить последнее ([math]n[/math]-е) дерево, т.к. после него все деревья можно будет пилить бесплатно (т.к. [math]c[n] = 0[/math]). Посчитаем следующую динамику : [math]dp[i][/math] - минимальная стоимость, заплатив которую будет срублено дерево номер [math]i.[/math] Тогда [math]dp[i] = min_{j=0...i-1}(dp[j] + a[i] * c[j])[/math]. То есть понятно, что выгодно рубить сначала более дорогие и низкие деревья, а потом более высокие и дешевые (док-во этого факта оставляется читателям как несложное упражнение). Тогда переберем [math]j \lt i[/math] - индекс предыдущего срубленного дерева. Пусть мы его срубили оптимальным (в смысле денег) способом. Тогда просто [math]a[i][/math] раз уменьшим высоту дерева i на 1. Каждый такой раз будем платить [math]c[j][/math] за последующую заправку пилы. Итак, на сруб [math]i[/math]-го дерева мы заплатили [math]a[i]*c[j][/math]. 
Нетрудно видеть, что такая динамика работает за [math]O(n^2)[/math]

О-Оптимизация

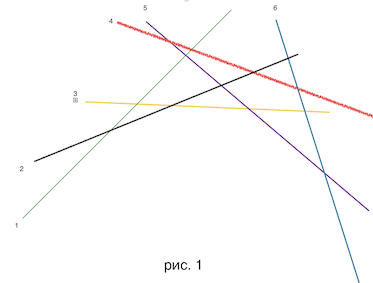
Давайте обозначим [math]dp[j][/math] за [math]b[j][/math], [math]а[i][/math] за [math]x[i][/math], а [math]c[j][/math] за [math]k[j][/math]. Теперь формула приняла вид [math]dp[i] = min_{j=0...i-1}(k[j]*x[i] + b[j])[/math]. Выражение [math]k[j]*x + b[j][/math] напоминает уравнение прямой [math]y = kx + b[/math]. Сопоставим каждому [math]j[/math], обработанному ранее прямую [math]y[j](x) = k[j]*x + b[j][/math]. Из условия «[math]c[i][/math] убывают [math]\lt =\gt k[j][/math] уменьшаются с номером [math]j[/math]» следует то, что прямые, полученные ранее отсортированы в порядке убывания углового коэффициент. Давайте нарисуем несколько таких прямых :

Итак, давайте выделим множество точек [math](x0, y0)[/math] , таких что все они принадлежат одной из прямых и при этом нету ни одной прямой [math]y’(x)[/math], такой что [math]y’(x0) \lt y0[/math]. Иными словами возьмем «выпуклую (вверх) оболочку» нашего множества прямых. На картинке множество точек выделено жирным оранжевым цветом и представляет собой выпуклую вверх функцию. Назовем ее «[math]y = convex(x)[/math]»

Для чего нам нужна эта выпуклая оболочка прямых?

Пусть мы считаем динамику для [math]i[/math]-го дерева. Его задает [math]x[i][/math]. Итак, нам нужно для данного [math]x[i][/math] найти минимум по всем [math]min_{j=0..i-1}(k[j]*x[i] + b[i]) = min_{j=0..i-1}(y[j](x[i]))[/math]. Нетрудно видеть, что это есть convex(x[i]). Из монотонности угловых коэффицентов отрезков, задающих выпуклую оболочку, и их расположения по координаты x следует то, что отрезок, который пересекает прямую [math]x = x[i][/math], можно найти бинарным поиском. Это потребует O(logn) времени на поиск такого j, что dp[i] = k[j] * x[i] + b[j]. Теперь осталось научиться быстро поддерживать множество прямых и добавлять [math]i[/math]-ю прямую после того, как мы посчитали [math]b[i] = dp[i][/math]. Название статьи подсказывает, что нужно воспользоваться алгоритмом построения выпуклой оболочки множества точек. Но (внезапно) у нас не точки, а прямые… Но что меняется??? Пусть есть 2 стека [math]k[] и b[][/math], которые задают прямые в отсортированном порядке. Пусть пришла новая прямая. Найдем точки пересечения (по x) с последними 2мя прямыми из стека. Назовем их [math]xL[/math] и [math]xR[/math]. Если оказалось, что новая прямая пересекает предпоследнюю прямую выпуклой оболочки позже, чем последнюю (xL >= xR), то последнюю можно удалить из нашего множества. Так будем делать, пока либо кол-во прямых в стеке не станет равным 2 или [math]xL[/math] не станет меньше [math]xR.[/math] Асимптотика : аналогично обычному алгоритму построения выпуклой оболочки, каждая прямая ровно 1 раз добавится в стек и максимум 1 раз удалится. Значит время работы перестройки выпуклой оболочки займет [math]O(n)[/math] суммарно. Корректность : достаточно показать, что прямую нужно удалить из множества т.и т.т., когда она последнюю прямую множества наша новая прямая пересекает ее в точке с координатой по оси X, меньшей, чем предпоследнюю.

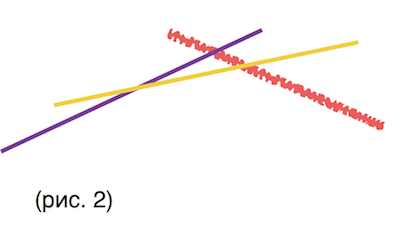
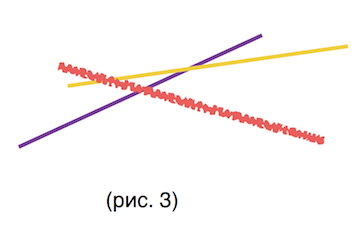
Действительно, пусть новая прямая пересекает последнюю прямую множества позже, чем предпоследнюю (рис.2 - красная прямая новая, фиолетовая - предпоследняя, желтая - последняя), то найдется такой отрезок [math][x1;x2][/math], что последняя(желтая) прямая при этих x-ах лежит ниже всех остальных и ее следует оставить в множестве. Теперь пусть новая прямая пересекает последнюю прямую множества раньше, чем предпоследнюю (рис.1), последняя прямая при любых x лежит выше какой-то другой прямой множества и значит ее можно удалить, чтд.

Детали реализации:

Будем хранить 2 массива (имитирующих стеки) : [math]front[][/math] и [math]st[][/math] - начало (по x) соответствующей прямой выпуклой оболочки и номер этой прямой (в глобальной нумерации). Также воспользуемся тем, что [math]x[i] = a[i][/math] возрастают (по условию задачи), а значит мы можем искать первое такое [math]j[/math], что [math]x[i] \gt = front[j][/math] не бинарным поиском, а методом 2х указателей за [math]O(n)[/math] суммарно. Также массив front[] можно хранить в целых числах, округляя х-координаты в сторону лежащих правее по оси x до ближайшего целого (*). Почему так? На самом деле мы, считая динамику, подставляем в уравнения прямых только целые [math]x[i][/math], а значит если [math]k[/math]-я прямая пересекается с [math]k+1[/math]-й в точке [math]z +[/math] [math]\alpha[/math] (z-целое, [math]\alpha[/math] [math]\in[/math] [math][0;1)[/math]), то мы будем подставлять [math]z[/math] или [math]z + 1[/math]. Поэтому можно считать, что новая прямая имеет "область действия", начиная с [math]z+1[/math]

Р.Реализация

            void Convex-hull-trick
            st[0] = 0
            from[0] = -[math]\infty[/math]// первая прямая покрывает все x-ы, начиная с -∞ 
            sz = 1 // текущий размер выпуклой оболочки 
            pos = 0 // текущая позиция первго такого j, что x[i] >= front[st[j]] 
            for  i = 1..n-1  {
                   	while (front[pos] < x[i]) // метод 1 указателя (ищем первое pos, такое что x[i] покрывается "областью действия" st[pos]-той прямой 
                   			++pos
                   	j = st[pos]
                    	dp[i] = K[j] * a[i] + B[j] 
                    	if (i < n - 1) {  // если у нас добавляется НЕ последняя прямая, то придется пересчитать выпуклую оболочку 
                       		K[i] = c[i]  // наши переобозначения переменных 
                       		B[i] = dp[i] // наши переобозначения переменных 
                        	        x = -[math]\infty[/math] 
                        	        while (1) {
            		                      j = st[sz - 1]
              		                      x = divide(B[j] - B[i], K[i] - K[j]) // x-координата пересечения с последней прямой оболочки, округленное в нужную сторону (*) 
            	 	                      if (x > from[sz - 1]) break  // перестаем удалять последнюю прямую из множества, если новая прямая пересекает ее позже, чем начинается ее "область действия" 
              	              	              --sz // удаляем последнюю прямую, если она лишняя 
                                       }
                                       st[sz] = i  
                                       from[sz++] = x // добавили новую прямую 
                    	}                       
            }          

(Здесь функция divide(a, b) возвращает нужное(*) округление a / b) Такая реализация будет работать за O(n).

Динамический convex hull trick

Заметим, что условия на прямые, что [math]k[i][/math] возрастает/убывает и [math]x[i][/math] убывает/возрастает выглядят не достаточно общими. Как же быть, если в задаче таких ограничений нет. Иногда можно отсортировать прямые нужным образом, не испортив свойств задачи (пример : задача G отсюда http://neerc.ifmo.ru/school/camp-2016/problems/20160318a.pdf). Но рассмотрим общий случай. Наша задача поменялась следующим образом : по-прежнему у нас есть выпуклая оболочка, имея которую мы за [math]O(logn)[/math] или быстрее можем найти [math]dp[i][/math], но теперь вставку i-й прямой в оболочку уже нельзя выполнить старым способом за [math]O(1)[/math] (в среднем). У нас есть выпуклая оболочка, наша прямая пересекает ее, возможно, «отрезая» несколько отрезков выпуклой оболочки в середине (рис. 4).

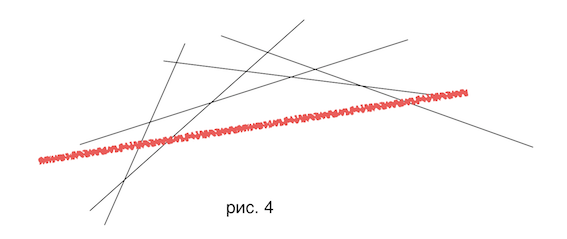
Т.е. нужно уметь быстро (за [math]O(logn)[/math]?) назодить, после какой прямой стоит пытаться вставить текущую (красную рис.4) примую и удалять лишние справа, начиная с нее, потом проводить аналогичные операции слева. Итак, давайте хранить [math]std::set[/math] (или любой аналог в других языках) пар [math]\lt k, st\gt [/math] = <коэффицент прямой, ее номер в глобальной нумерации>. Когда приходит новая прямая, делаем lower_bound - 1 в сете, т.е. ищем ближайшую прямую с меньшим углом наклона, и начиная с нее повторяем старый алгоритм (удаляем, пока прямая бесполезная). И симметричный алгоритм применяем ко всем прямым справа от нашей. Асимптотика решения составит [math]O(logn)[/math] на каждый из n запросов «добавить прямую» + [math]O(n)[/math] суммарно на удаление прямых. Итго [math]O(nlogn)[/math].

Альтернативный подход

Другой способ интерпретировать выражение [math]dp[i] = max(dp[j] + a[i] * c[j])[/math] по всем их заключается в следующем: давайте перепишем выражение [math]dp[j] + a[i] * c[j] = (dp[j], c[j]) * (1, a[i])[/math], т.е. запишем ка скалярное произведение векторов [math]v[j] = (dp[j], c[j]) и u[i] = (1, a[i])[/math]. Вектора [math]v[j] = (dp[j], c[j])[/math] хотелось бы организовать так, чтобы за [math]O(logn)[/math] находить максимизирующий выражение [math]v[j] * u[i][/math]. Посмотрим на рис. 5. Заметим довольно очевидный факт : красная точка(вектор) [math]j[/math] не может давать более оптимальное значение [math]v[j] * u[i][/math] одновременно чем обе синие точки, т.к. [math]v[j] * u[i][/math] - это на самом деле проекция вектора [math]v[j][/math] на [math]u[i][/math]. По этой причине нам достаточно оставить выпуклую оболочку векторов [math]v[j][/math], а ответ на запрос - это поиск [math]v[j][/math], максимизирующего проекцию на [math]u[i][/math]. Это задача поиска ближайшей точки выпуклого многоугольника (составленного из точек выпуклой оболочки) к заданной прямой (из [math](0, 0)[/math] в [math](1, a[i])[/math]). Ее можно решить за O(logn) двумя бинарными или одним тернарным поиском Асимптотика алгоритма по-прежнему составит [math]O(n*log(n))[/math]