Группы графов — различия между версиями
Ashkroft (обсуждение | вклад) |
Ashkroft (обсуждение | вклад) |
||
| Строка 32: | Строка 32: | ||
Вершинная группа графа G индуцирует другую группу подстановок <tex> \Gamma_1 (G) </tex>, называемую '''реберной группой графа''' <tex>G</tex>; она действует на множестве ребер <tex>E(G)</tex>. | Вершинная группа графа G индуцирует другую группу подстановок <tex> \Gamma_1 (G) </tex>, называемую '''реберной группой графа''' <tex>G</tex>; она действует на множестве ребер <tex>E(G)</tex>. | ||
}} | }} | ||
| − | [[Файл:fordm.png|200px| | + | |
| + | [[Файл:fordm.png|thumb|200px|right]] | ||
| + | |||
| + | Для иллюстрации различия групп <tex>\Gamma</tex> и <tex>\Gamma_1</tex> рассмотрим граф <tex>K_4 - х</tex>, показанный на рисунке; его вершины помечены <tex>v_1 , v_2, v_3, v_4 </tex> а ребра <tex>x_1, x_2, x_3, x_4, x_5 </tex>. Вершинная группа <tex>\Gamma (K_4 - x) </tex> состоит из четырех подстановок | ||
| + | <tex>(v_1)(v_2)(v_3)(v_4); (v_1)(v_3)(v_2v_4); (v_2)(v_4)(v_1v_3); (v_1v_3)(v_2v_4).</tex> | ||
| + | |||
| + | Тождественная подстановка вершинной группы индуцирует тождественную подстановку на множестве ребер, в то время как подстановка <tex>(v_1)(v_3)(v_2v_4)</tex> индуцирует подстановку на множестве ребер, в которой ребро <tex>x_5</tex> остается на месте, <tex>х_1</tex> меняется с <tex>х_4</tex>, а <tex>х_2</tex> с <tex>х_3</tex>. Таким образом, реберная группа <tex>\Gamma_1 (K_4 - x) </tex> состоит из следующих подстановок, индуцируемых указанными выше элементами вершинной группы: | ||
| + | <tex>(x_1)(x_2)(x_3)(x_4)(x_5); (x_1x_4)(x_2x_3)(x_5); (x_1x_2)(x_3x_4)(x_5); (x_1x_3)(x_2x_4)(x_5).</tex> | ||
| + | |||
| + | Понятно, что реберная и вершинная группы графа <tex>K_4 - х</tex> изоморфны. Но они, конечно, не могут быть идентичными, так как степень группы <tex>\Gamma_1 (K_4 - x) </tex> равна 5, а степень группы <tex>\Gamma (K_4 - x) </tex> равна 4. | ||
| + | |||
==Источники информации== | ==Источники информации== | ||
* Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.) | * Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.) | ||
Версия 18:14, 29 ноября 2016
| Определение: |
Непустое множество А вместе с заданной на нем бинарной операцией, результат применения которой к элементам и из обозначается через , образует группу, если выполняются следующие четыре аксиомы:
|
| Определение: |
| Подстановка — взаимно однозначное отображение конечного множества на себя. |
| Определение: |
| Если некоторая совокупность подстановок замкнута относительно композиции отображений, определяющей бинарную операцию для подстановок на одном и том же множестве, то аксиомы 2, 3 и 4 автоматически выполняются и эта совокупность называется группой подстановок. |
| Определение: |
| Автоморфизмом графа называется изоморфизм графа на себя |
| Определение: |
| Каждый автоморфизм графа есть подстановка множества вершин , сохраняющая смежность. Конечно, подстановка переводит любую вершину графа в вершину той же степени. Очевидно, что последовательное выполнение двух автоморфизмов есть также автоморфизм; поэтому автоморфизмы графа образуют группу подстановок , действующую на множестве вершин . Эту группу называют группой или иногда вершинной группой графа . |
| Определение: |
| Вершинная группа графа G индуцирует другую группу подстановок , называемую реберной группой графа ; она действует на множестве ребер . |
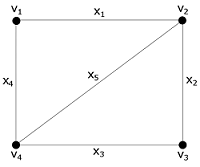
Для иллюстрации различия групп и рассмотрим граф , показанный на рисунке; его вершины помечены а ребра . Вершинная группа состоит из четырех подстановок
Тождественная подстановка вершинной группы индуцирует тождественную подстановку на множестве ребер, в то время как подстановка индуцирует подстановку на множестве ребер, в которой ребро остается на месте, меняется с , а с . Таким образом, реберная группа состоит из следующих подстановок, индуцируемых указанными выше элементами вершинной группы:
Понятно, что реберная и вершинная группы графа изоморфны. Но они, конечно, не могут быть идентичными, так как степень группы равна 5, а степень группы равна 4.
Источники информации
- Харари Ф. Теория графов. М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296 с.)