Обход в глубину, цвета вершин — различия между версиями
(→Дерево обхода в глубину) |
|||
| Строка 1: | Строка 1: | ||
| − | '''Обход в глубину''' (поиск в глубину, англ. | + | '''Обход в глубину''' (поиск в глубину, англ. ''Depth-First Search'', ''DFS'') — один из основных методов обхода [[Основные определения теории графов|графа]], часто используемый для [[Использование обхода в глубину для проверки связности|проверки связности]], поиска [[Использование обхода в глубину для поиска цикла в ориентированном графе|цикла]] и [[Использование обхода в глубину для поиска компонент сильной связности|компонент сильной связности]] и для [[Использование обхода в глубину для топологической сортировки|топологической сортировки]]. |
== Алгоритм == | == Алгоритм == | ||
| Строка 14: | Строка 14: | ||
=== Реализация === | === Реализация === | ||
| − | + | В массиве <tex>visited[]</tex> хранится информация о ''пройденных'' и ''не пройденных'' вершинах. | |
| − | + | ||
| − | + | '''function''' dfs(u: '''int'''): | |
| − | + | visited[u] = true | |
| − | + | '''for''' v: (u, v) '''in''' G | |
| − | + | '''if''' '''not''' visited[v] | |
| − | + | dfs(v) | |
| − | + | ||
| − | + | Вызов обхода в глубину из основной программы осуществляется так: | |
| − | + | '''function''' main(): '''int''' | |
| − | + | <font color=darkgreen>//задание графа G с количеством вершин n </font> | |
| − | + | '''fill'''(visited, false) | |
| − | + | '''for''' i = 1 '''to''' n | |
| − | + | '''if''' '''not''' visited[i] | |
| − | + | dfs(i) | |
| − | |||
| − | |||
| − | |||
| − | |||
=== Время работы === | === Время работы === | ||
| Строка 38: | Строка 34: | ||
== Цвета вершин == | == Цвета вершин == | ||
| − | Зачастую, простой информации "были/не были в вершине" не хватает для конкретных целей. | + | Зачастую, простой информации "были/не были в вершине" не хватает для конкретных целей. |
| − | Поэтому в процессе алгоритма вершинам задают некоторые цвета: | + | |
| − | + | Поэтому в процессе алгоритма вершинам задают некоторые цвета: | |
| − | + | ||
| − | + | *если вершина ''белая'', значит, мы в ней еще не были, вершина ''не пройдена''; | |
| + | *''серая'' — вершина ''проходится'' в текущей процедуре <tex>dfs</tex>; | ||
| + | *''черная'' — вершина ''пройдена'', все итерации <tex>dfs</tex> от нее завершены. | ||
Такие "метки" в основном используются при [[Использование обхода в глубину для поиска цикла в ориентированном графе|поиске цикла]]. | Такие "метки" в основном используются при [[Использование обхода в глубину для поиска цикла в ориентированном графе|поиске цикла]]. | ||
=== Реализация === | === Реализация === | ||
| − | Отличие реализации с цветами от предыдущей лишь в массиве visited, который мы назовем теперь color. | + | Отличие реализации с цветами от предыдущей лишь в массиве <tex>visited[]</tex>, который мы назовем теперь <tex>color[]</tex>. В нем будет хранится информация о цветах вершин. |
| + | |||
| + | '''function''' dfs(u: '''int'''): | ||
| + | color[u] = ''gray'' | ||
| + | '''for''' v: (u, v) '''in''' G | ||
| + | '''if''' color[v] == ''white'' | ||
| + | dfs(v) | ||
| + | color[u] = ''black'' | ||
| + | |||
| + | Вызов обхода в глубину из основной программы осуществляется так: | ||
| + | '''function''' main(): '''int''' | ||
| + | <font color=darkgreen>//задание графа G с количеством вершин n </font> | ||
| + | '''fill'''(color, ''white'') | ||
| + | '''for''' i = 1 '''to''' n | ||
| + | '''if''' color[i] == ''white'' | ||
| + | dfs(i) | ||
| + | |||
| + | === Пример === | ||
| + | Рассмотрим, как будут изменяться цвета вершин при обходе в глубину данного графа. | ||
| − | + | {| style="background-color:#CCC;margin:0.5px;width:600px" | |
| − | + | !style="background-color:#EEE"| Описание шага | |
| − | + | !style="background-color:#EEE"| Состояние графа | |
| − | + | |- | |
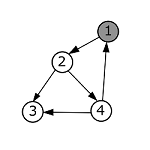
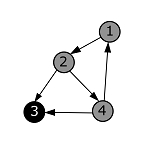
| − | + | |style="background-color:#FFF;padding:2px 10px"| Из основной программы проверяем, что первая вершина окрашена в белый цвет. Заходим в нее и раскрашиваем ее в серый цвет. | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs1.png|150px|]] | |
| − | + | |- | |
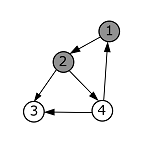
| − | + | |style="background-color:#FFF;padding:2px 10px"| Пробуем пойти в вершину с номером 2. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs2.png|150px|]] | |
| − | + | |- | |
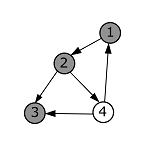
| − | + | |style="background-color:#FFF;padding:2px 10px"| Пробуем пойти в вершину с номером 3. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs3.png|150px|]] | |
| − | + | |- | |
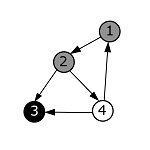
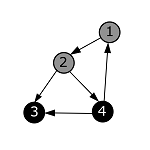
| − | + | |style="background-color:#FFF;padding:2px 10px"| Проверяем, что из вершины с номером 3 не исходит ни одного ребра. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2. | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs4.png|150px|]] | |
| − | + | |- | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| Пробуем пойти в вершину с номером 4. Проверяем, что она белая, и переходим в нее. Окрашиваем ее в серый цвет. | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs5_6_7.png|150px|]] | |
| − | + | |- | |
| − | + | |style="background-color:#FFF;padding:2px 10px"| Пробуем пойти в вершину с номером 3. Видим, что она черного цвета, и остаемся на месте. | |
| + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs5_6_7.png|150px|]] | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 10px"| Пробуем пойти в вершину с номером 1. Видим, что она серого цвета, и остаемся на месте. | ||
| + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs5_6_7.png|150px|]] | ||
| + | |- | ||
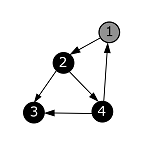
| + | |style="background-color:#FFF;padding:2px 10px"| Из вершины с номером 4 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 2. | ||
| + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs8.png|150px|]] | ||
| + | |- | ||
| + | |style="background-color:#FFF;padding:2px 10px"| Из вершины с номером 2 больше нет исходящих ребер. Помечаем ее в черный цвет и возвращаемся в вершину с номером 1. | ||
| + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs9.png|150px|]] | ||
| + | |- | ||
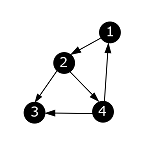
| + | |style="background-color:#FFF;padding:2px 10px"| Из вершины с номером 1 больше нет исходящих ребер. Помечаем ее в черный цвет и выходим в основную программу. Из основной программы проверяем, что все вершины окрашены в черный цвет. Алгоритм завершен. | ||
| + | |style="background-color:#FFF;padding:2px 10px"| [[Файл:dfs10.png|150px|]] | ||
| + | |} | ||
== Дерево обхода в глубину == | == Дерево обхода в глубину == | ||
| Строка 87: | Строка 117: | ||
* Черный цвет, соответственно, указывает на ''прямое'' или ''перекрестное ребро''. | * Черный цвет, соответственно, указывает на ''прямое'' или ''перекрестное ребро''. | ||
| − | == Источники == | + | == Источники информации == |
| − | *[http://ru.wikipedia.org/wiki/Поиск_в_глубину | + | *[http://ru.wikipedia.org/wiki/Поиск_в_глубину Википедия {{---}} Поиск в глубину] |
| − | *[http://en.wikipedia.org/wiki/Depth-first_search | + | *[http://en.wikipedia.org/wiki/Depth-first_search Wikipedia {{---}} Depth-first search] |
*[http://www.e-maxx.ru/algo/dfs Обход в глубину. Реализации.] | *[http://www.e-maxx.ru/algo/dfs Обход в глубину. Реализации.] | ||
* Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, второе издание. Пер. с англ. — Издательский дом "Вильямс", 2007. — 1296 с. — Глава 22. Элементарные алгоритмы для работы с графами. | * Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, второе издание. Пер. с англ. — Издательский дом "Вильямс", 2007. — 1296 с. — Глава 22. Элементарные алгоритмы для работы с графами. | ||
Версия 22:53, 11 декабря 2016
Обход в глубину (поиск в глубину, англ. Depth-First Search, DFS) — один из основных методов обхода графа, часто используемый для проверки связности, поиска цикла и компонент сильной связности и для топологической сортировки.
Содержание
Алгоритм
Общая идея
Общая идея алгоритма состоит в следующем: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них.
Пошаговое представление
- Выбираем любую вершину из еще не пройденных, обозначим ее как .
- Запускаем процедуру
- Помечаем вершину как пройденную
- Для каждой не пройденной смежной с вершиной (назовем ее ) запускаем
- Повторяем шаги 1 и 2, пока все вершины не окажутся пройденными.
Реализация
В массиве хранится информация о пройденных и не пройденных вершинах.
function dfs(u: int):
visited[u] = true
for v: (u, v) in G
if not visited[v]
dfs(v)
Вызов обхода в глубину из основной программы осуществляется так:
function main(): int
//задание графа G с количеством вершин n
fill(visited, false)
for i = 1 to n
if not visited[i]
dfs(i)
Время работы
Оценим время работы обхода в глубину. Процедура вызывается от каждой вершины не более одного раза, а внутри процедуры рассматриваются все такие ребра . Всего таких ребер для всех вершин в графе , следовательно, время работы алгоритма оценивается как .
Цвета вершин
Зачастую, простой информации "были/не были в вершине" не хватает для конкретных целей.
Поэтому в процессе алгоритма вершинам задают некоторые цвета:
- если вершина белая, значит, мы в ней еще не были, вершина не пройдена;
- серая — вершина проходится в текущей процедуре ;
- черная — вершина пройдена, все итерации от нее завершены.
Такие "метки" в основном используются при поиске цикла.
Реализация
Отличие реализации с цветами от предыдущей лишь в массиве , который мы назовем теперь . В нем будет хранится информация о цветах вершин.
function dfs(u: int):
color[u] = gray
for v: (u, v) in G
if color[v] == white
dfs(v)
color[u] = black
Вызов обхода в глубину из основной программы осуществляется так:
function main(): int
//задание графа G с количеством вершин n
fill(color, white)
for i = 1 to n
if color[i] == white
dfs(i)
Пример
Рассмотрим, как будут изменяться цвета вершин при обходе в глубину данного графа.
Дерево обхода в глубину
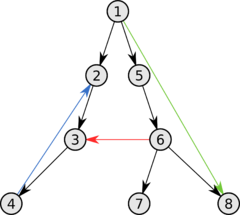
Рассмотрим подграф предшествования обхода в глубину , где , где в свою очередь — вершина, от которой был вызван (для вершин, от которых был вызван нерекурсивно это значение соответственно равно ). Подграф предшествования поиска в глубину образует лес обхода в глубину, который состоит из нескольких деревьев обхода в глубину. С помощью полученного леса можно классифицировать ребра графа :
- Ребрами дерева назовем те ребра из , которые вошли в .
- Ребра , соединяющие вершину с её предком в дереве обхода в глубину назовем обратными ребрами (для неориентированного графа предок должен быть не родителем, так как иначе ребро будет являться ребром дерева).
- Ребра , не являющиеся ребрами дерева и соединяющие вершину с её потомком в дереве обхода в глубину назовем прямыми ребрами (в неориентированном графе нет разницы между прямыми и обратными ребрами, поэтому все такие ребра считаются обратными).
- Все остальные ребра назовем перекрестными ребрами — такие ребра могут соединять вершины одного и того же дерева обхода в глубину, когда ни одна из вершин не является предком другой, или соединять вершины в разных деревьях.
Алгоритм можно модифицировать так, что он будет классифицировать встречающиеся при работе ребра. Ключевая идея состоит в том, что каждое ребро можно классифицировать при помощи цвета вершины при первом его исследовании, а именно:
- Белый цвет вершины по определению говорит о том, что это ребро дерева.
- Серый цвет в силу того, что серые вершины всегда образуют нисходящий путь в каком-либо из деревьев и встреченная вершина лежит на нем выше вершины , определяет обратное ребро (для неориентированного графа необходимо проверить условие ).
- Черный цвет, соответственно, указывает на прямое или перекрестное ребро.
Источники информации
- Википедия — Поиск в глубину
- Wikipedia — Depth-first search
- Обход в глубину. Реализации.
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, второе издание. Пер. с англ. — Издательский дом "Вильямс", 2007. — 1296 с. — Глава 22. Элементарные алгоритмы для работы с графами.