AA-дерево — различия между версиями
(Новая страница: «'''АA-дерево''' (англ. ''AA-Tree'') {{---}} структура данных, представляющая собой сбалансированное [...») |
|||
| Строка 1: | Строка 1: | ||
'''АA-дерево''' (англ. ''AA-Tree'') {{---}} структура данных, представляющая собой сбалансированное [[Дерево поиска, наивная реализация|двоичное дерево поиска]], которое является разновидностью красно-черного дерева с дополнительными ограничениями. | '''АA-дерево''' (англ. ''AA-Tree'') {{---}} структура данных, представляющая собой сбалансированное [[Дерево поиска, наивная реализация|двоичное дерево поиска]], которое является разновидностью красно-черного дерева с дополнительными ограничениями. | ||
| − | АA-дерево названо по первым буквам имени и | + | АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию B-дерева в 1993 году. |
{{Определение | {{Определение | ||
| Строка 27: | Строка 27: | ||
== Балансировка == | == Балансировка == | ||
Для балансировки АА-дерева нужно две операции: | Для балансировки АА-дерева нужно две операции: | ||
| − | #'''Skew(p)''' - устранение левого ребра, соединяющего вершину ''p'' с вершиной того же уровня, что у ''p''. | + | #'''Skew(p)''' {{---}} устранение левого ребра, соединяющего вершину ''p'' с вершиной того же уровня, что у ''p''. |
| − | #'''Split(p)''' - | + | |
| + | [[Файл: Skew.png]] | ||
| + | |||
| + | |||
| + | '''function''' skew '''is''' | ||
| + | '''input''': T, a node representing an AA tree that needs to be rebalanced. | ||
| + | '''output''': Another node representing the rebalanced AA tree. | ||
| + | |||
| + | '''if''' T == NULL '''then''' | ||
| + | '''return''' NULL | ||
| + | '''else''' '''if''' left(T) == NULL '''then''' | ||
| + | '''return''' T | ||
| + | '''else''' '''if''' level(left(T)) == level(T) '''then''' | ||
| + | Swap the pointers of horizontal left links. | ||
| + | L = left(T) | ||
| + | left(T) := right(L) | ||
| + | right(L) := T | ||
| + | '''return''' L | ||
| + | '''else''' | ||
| + | '''return''' T | ||
| + | '''end''' '''if''' | ||
| + | '''end''' '''function''' | ||
| + | |||
| + | |||
| + | #'''Split(p)''' {{---}} устранение двух последовательных правых ребер, которые соединяют вершины с одним уровнем. | ||
| + | |||
| + | [[Файл: Split_rb.png]] | ||
| + | |||
| + | '''function''' split '''is''' | ||
| + | '''input''': T, a node representing an AA tree that needs to be rebalanced. | ||
| + | '''output''': Another node representing the rebalanced AA tree. | ||
| + | |||
| + | '''if''' nil(T) '''then''' | ||
| + | '''return''' Nil | ||
| + | '''else''' '''if''' nil(right(T)) '''or''' nil(right(right(T))) '''then''' | ||
| + | '''return''' T | ||
| + | '''else''' '''if''' level(T) == level(right(right(T))) '''then''' | ||
| + | We have two horizontal right links. Take the middle node, elevate it, and return it. | ||
| + | R = right(T) | ||
| + | right(T) := left(R) | ||
| + | left(R) := T | ||
| + | level(R) := level(R) + 1 | ||
| + | '''return''' R | ||
| + | '''else''' | ||
| + | '''return''' T | ||
| + | '''end''' '''if''' | ||
| + | '''end function''' | ||
Версия 22:39, 19 декабря 2016
АA-дерево (англ. AA-Tree) — структура данных, представляющая собой сбалансированное двоичное дерево поиска, которое является разновидностью красно-черного дерева с дополнительными ограничениями.
АA-дерево названо по первым буквам имени и фамилии изобретателя, Арне Андерссона, который впервые предложил данную модификацию B-дерева в 1993 году.
| Определение: |
| Уровень вершины (англ. Level) - вертикальная высота соответствующей вершины. Уровень листа равен 1. |
В отличие от красно-черных деревьев, к одной вершине можно присоединить вершину только того же уровня, только одну и только справа (другими словами, красные вершины могут быть добавлены только в качестве правого ребенка).
Свойства
- Уровень каждого листа равен 1.
- Уровень каждого левого ребенка ровно на один меньше, чем у его родителя.
- Уровень каждого правого ребенка равен или один меньше, чем у его родителя.
- Уровень каждого правого внука строго меньше, чем у его прародителя.
- Каждая вершина с уровнем больше 1 имеет двоих детей.
Для поддержки баланса красно-черного дерева необходимо обрабатывать 7 различных вариантов расположения вершин:
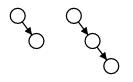
В АА-дереве из-за строгих ограничений необходимо обрабатывать только два вида возможных расположений вершин:
Балансировка
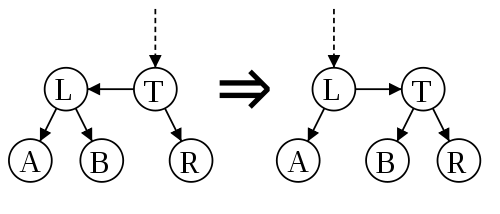
Для балансировки АА-дерева нужно две операции:
- Skew(p) — устранение левого ребра, соединяющего вершину p с вершиной того же уровня, что у p.
function skew is
input: T, a node representing an AA tree that needs to be rebalanced.
output: Another node representing the rebalanced AA tree.
if T == NULL then
return NULL
else if left(T) == NULL then
return T
else if level(left(T)) == level(T) then
Swap the pointers of horizontal left links.
L = left(T)
left(T) := right(L)
right(L) := T
return L
else
return T
end if
end function
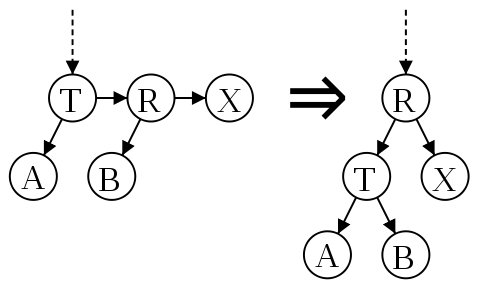
- Split(p) — устранение двух последовательных правых ребер, которые соединяют вершины с одним уровнем.
function split is
input: T, a node representing an AA tree that needs to be rebalanced.
output: Another node representing the rebalanced AA tree.
if nil(T) then
return Nil
else if nil(right(T)) or nil(right(right(T))) then
return T
else if level(T) == level(right(right(T))) then
We have two horizontal right links. Take the middle node, elevate it, and return it.
R = right(T)
right(T) := left(R)
left(R) := T
level(R) := level(R) + 1
return R
else
return T
end if
end function