Сетевая безопасность

Понятие сетевой безопасности

К сожалению, суровая правда жизни заключается в том, что изначально сеть интернет не создавалась с большим учетом безопасности. Поэтому никогда нельзя забывать о сетевой угрозе.

Сама по себе сетевая безопасность включает в себя 3 основных аспекта:

1. Как взломщики могут атаковать компьютерные сети
2. Как можно защитить компьютерные сети от атак
3. Как разработать архитектуру сети, чтобы она была устойчива к атакам

Вредоносное ПО

Злоумышленник может передать вредоносное ПО на компьютер по сети интернет с помощью вируса, червя или Троянского коня. После этого у злоумышленника есть несколько возможностей использования зараженного компьютера, в основном следующие:

1. Шпионское ПО может записывать все нажатые клавиши на клавиатуре, посещенные веб-сайты и передавать их злоумышленнику, например, с целью хищения паролей
2. Зараженный компьютер может использоваться ботнетом для спам или DDoS-атак
3. Часто вредоносное ПО реплицируется и передается с зараженного компьютера дальше еще не зараженным

Троянский конь

Представляет собой инструкции, спрятанные внутри обычной программы, которые выполняют вредоносный код в интересах создателя. По сути это означает, что Троянский конь маскируется под программы, необходимые пользователю, и исполняет вредоносный код во время работы программы.

Вирус

Представляет собой набор инструкций, который во время исполнения вставляет свои копии в другие программы. Например, код в электронных сообщениях, который во время исполнения отсылает сам себя другим пользователям по электронной почте.

Червь

По сути очень похож на вирус, но отличается тем, что вместо репликации в других программах в пределах компьютера, червь распространяется по другим машинам в сети.

Логическая бомба

Представляет собой набор инструкций, который исполняется при определенных условиях в будущем, например, по наступлению какого-то определенного времени.

Зомби

Зомби по сути есть компьютер, на который установлен набор вредоносных инструкций, готовый исполниться и атаковать другой компьютер по сигналу от создателя. Обеспечивает лучшую анонимность злоумышленника, чем прямая атака. Часто такой набор инструкций устанавливается на большое число компьютеров, делая их зомби, а потом все они атакуют какой-то определенный компьютер.

Типы сетевых атак

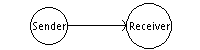
Нормальный поток данных

Нормальный поток данных выглядит идейно следующим образом:

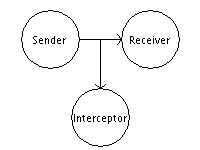
Прерывание потока данных

По сути это атака на доступность какого-либо ресурса (DDoS (Distributed Denial of Service) атаки). Выглядит примерно так:

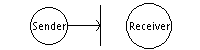
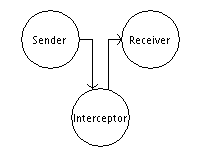
Перехват данных

Эта атака происходит с целью похищения каких-либо конфиденциальных данных, при этом не меняя их. Изобразить можно следующим образом:

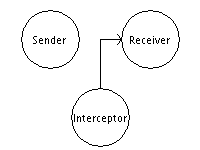
Модификация потока данных

Это атака на целостность данных. В данном случае трафик на середине пути перехватывается и злоумышленник подменяет его на другой, который пойдет в итоге получателю. То есть изобразить такую передачу данных можно следующим образом:

Фабрикация данных

Данная атака производится на целостность данных, то есть трафик маскируется под настоящий, заставляя получателя думать, что он подлинный. В итоге получатель передает свои данные злоумышленнику. Выглядит это так:

Подходы сетевой безопасности

Криптография

Допустим, что Алиса и Боб общаются между собой, а кто-то другой имеет возможность перехватить, удалить или добавить любое сообщение. Алиса и Боб хотят общаться безопасно, чтобы никто не мог им помешать. Тут на помощь им приходят алгоритмы криптографии.

В данном случае нам нужны такие ключи [math]K_{A}[/math] и [math]K_{B}[/math], что [math]m = K_{B}(K_{A}(m))[/math], где [math]m[/math] - исходное сообщение, а [math]K_{A}(m)[/math] - зашифрованное сообщение. Самое простое решение - использовать в качестве ключа некоторую другую перестановку алфавита, то есть словарь соответствия каждой букве какой-то другой. Минус такого подхода заключается в том, что очень быстро простым перебором можно подобрать ключ. Что же можно сделать? Разберемся, на чем основана криптография. Идея заключается в том, что алгоритм шифрования известен всем, а вот ключи являются секретными. Существует 2 основных типа криптографии: по симметричному ключу и по публичному ключу.

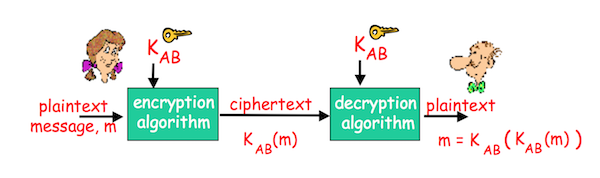
Шифрование по симметричному ключу

Оба собеседника используют один и тот же симметричный ключ. По факту у обоих есть ключ [math]K_{AB}[/math] такой, что [math]m = K_{AB}(K_{AB}(m))[/math], где [math]m[/math] - передаваемое сообщение, а [math]K_{AB}(m)[/math] - зашифрованное сообщение.

Есть 2 типа симметричного ключа:

1. Потоковый шифр - симметричный шифр, в котором каждый символ сообщения преобразуется в символ зашифрованного текста в зависимости от используемого ключа и его расположения в сообщении. Одним из самых популярных шифров данного типа является RC4. Он широко используется в алгоритмах обеспечения безопасности беспроводных сетей WEP и WPA, а также может использоваться в протоколах SSL и TLS. Этот шифр строится на основе генератора псевдослучайных битов. На вход генератора записывается ключ, а на выходе читаются псевдослучайные биты. Длина ключа может составлять от 40 до 2048 бит. Генерируемые биты при этом имеют равномерное распределение. Основными преимуществами RC4 являются высокая скорость работы и переменный размер ключа. При этом он довольно уязвим, если используются не случайные или связанные ключи или один ключевой поток используется дважды.
2. Блочный шифр - симметричный шифр, оперирующий группами бит фиксированной длины - блоками, характерный размер которых меняется в пределах 64-256 бит. Если исходный текст (или его остаток) меньше размера блока, перед шифрованием его дополняют. Фактически, блочный шифр представляет собой подстановку на алфавите блоков, которая, как следствие, может быть моно- или полиалфавитной. Главным достоинством блочных шифров является сходство алгоритмов шифрования и расшифрования, которые почти всегда отличаются лишь порядком действий. Блочный шифр сам по себе состоит из двух алгоритмов: шифрования и расшифрования. Оба алгоритма можно представить в виде функций. Функция шифрования [math]E[/math] (англ. encryption - шифрование) на вход получает блок данных [math]M[/math] (англ. message - сообщение) размером [math]n[/math] бит и ключ [math]K[/math] (англ. key - ключ) размером [math]k[/math] бит и на выходе отдает блок шифротекста [math]C[/math] (англ. cipher - шифр) размером [math]n[/math] бит: [math]E_{K}(M) := E(K, M) : \{0, 1\}^{k} \times \{0, 1\}^{n} \rightarrow \{0, 1\}^{n}[/math]. Для любого ключа [math]K[/math], [math]E_{K}[/math] является биекцией на множестве [math]n[/math]-битных блоков. Функция расшифрования [math]D[/math] (англ. decryption - расшифрование) на вход получает шифр [math]C[/math], ключ [math]K[/math] и на выходе отдает [math]M[/math]: [math]D_{K}(C) := D(K, C) : \{0, 1\}^{k} \times \{0, 1\}^{n} \rightarrow \{0, 1\}^{n}[/math], являясь, при этом, обратной к функции шифрования: [math]D = E^{-1}[/math], [math]\forall K : D_{K}(E_{K}(M)) = M[/math] и [math]E_{K}(D_{K}(C)) = C[/math]. Можно заметить, что ключ, необходимый для шифрования и дешифрования, один и тот же - следствие симметричности блочности шифра.

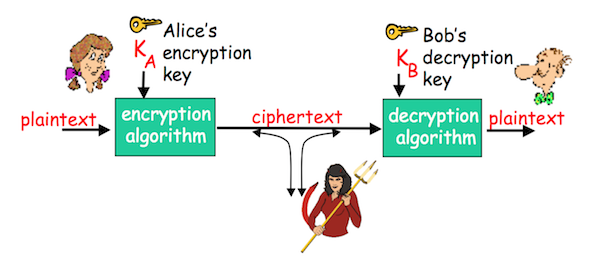
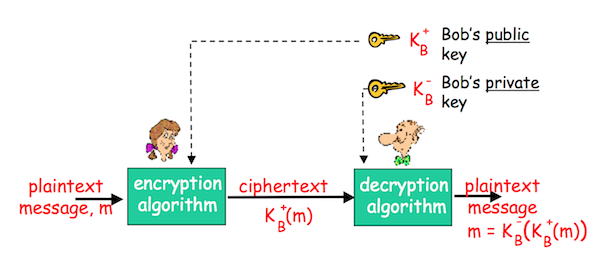
Шифрование по публичному ключу

Данный подход принципиально отличается от шифрования по симметричному ключу. Во-первых, у отправителя и получателя есть своя пара публичного и секретного ключа, при этом секретными ключами они не делятся даже друг с другом. Во-вторых, публичный ключ шифрования известен всем. И, наконец, приватный ключ дешифрования известен только получателю. Вот как это выглядит:

Можно сделать вывод, что должно выполняться 2 требования: [math]K_{B}^{-}[/math] и [math]K_{B}^{+}[/math] такие, что [math]K_{B}^{-}(K_{B}^{+}(m)) = m[/math], и, зная публичный ключ, человек не должен иметь возможности посчитать приватный. Одним из самых известных алгоритмов является RSA (Rivest-Shamir-Adleman). Это криптографический алгоритм с открытым ключом, который основывается на вычислительной сложности задачи факторизации больших целых чисел. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник создает свой открытый и закрытый ключ самостоятельно, при этом эти ключи являются согласованной парой в том смысле, что они являются взаимно обратными, то есть:

[math]\forall[/math] допустимых пар открытого и закрытого ключей [math](p, s)[/math]

[math]\exists[/math] соответствующие функции шифрования [math]E_{p}(x)[/math] и расшифрования [math]D_{s}(x)[/math] такие, что

[math]\forall[/math] сообщений [math]m \in M[/math], где [math]M[/math] - множество допустимых сообщений,

[math]m = D_{s}(E_{p}(m)) = E_{p}(D_{s}(m))[/math].

RSA-ключи генерируются следующим образом:

1. Выбираются два различных простых числа [math]p[/math] и [math]q[/math] заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение [math]n = p \cdot q[/math], которое называется модулем.
3. Вычисляется значение функции Эйлера от числа [math]n[/math]: [math]\phi (n) = (p - 1) \cdot (q - 1)[/math].
4. Выбирается целое число [math]e[/math] [math](1 \lt e \lt \phi (n))[/math], взаимно простое со значением функции [math]\phi (n)[/math]. Обычно в качестве [math]e[/math] берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма [math]17[/math], [math]257[/math] или [math]65537[/math]. Число [math]e[/math] называется открытой экспонентой.
5. Выбирается число [math]d[/math], мультипликативно обратное к числу [math]e[/math] по модулю [math]\phi (n)[/math], то есть число, удовлетворяющее сравнению: [math]d \cdot e \equiv 1 (mod\ \phi (n))[/math]. Число [math]d[/math] называется секретной экспонентой.
6. Пара [math]\{e, n\}[/math] публикуется в качестве открытого ключа RSA.
7. Пара [math]\{d, n\}[/math] играет роль закрытого ключа RSA и держится в секрете.

Теперь, чтобы зашифровать сообщение [math]m[/math], нужно посчитать [math]c = m^{e}\ mod\ n[/math], а чтобы расшифровать - [math]m = c^{d}\ mod\ n[/math]. Однако такая схема не используется на практике по причине того, что она не является практически надежной, так как односторонняя функция является детерминированной. Чтобы избежать такого, используют сеансовый ключ. С помощью RSA шифрования собеседники обмениваются симметричными ключами сессии, и дальше уже общаются с их помощью.