|
|
| Строка 1: |
Строка 1: |
| − | В математике '''гиперграф''' - это обобщение графа, у которого ребра могут соединять любое количество вершин. Более формально, гиперграф <tex>H</tex> - это пара <tex>(X, E)</tex> , где <tex>X</tex> - множество элементов называемых узлами или вершинами, и <tex>E</tex> - не пустое подмножество <tex>X</tex> называемых гиперребрами или просто ребрами.
| + | {{Определение |
| | + | |definition= |
| | + | Гиперграфом <tex>H</tex> называют такую пару <tex>H = (X, E)</tex> , где <tex>X</tex> - множество вершин, а <tex>E</tex> - семейство подмножеств X, называемых '''гиперребрами''' |
| | + | }} |
| | | | |
| − | В то время, как ребра графа соединяют две пары вершин, гиперребра - произвольные множества вершин, которые могут содержать любое количество вершин. Однако, очень часто рассматривают гиперграфы с гиперребрами одинаковой мощности ; <tex>k</tex> - равномерный гиперграф - это такой гиперграф, у которого все гиперребра имеют размер k. (Другими словами, такой гиперграф множество подмножеств, которые содержат k вершин). Так например, <tex>2</tex> - равномерный гиперграф - обычный граф.
| + | Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом. |
| | | | |
| − | [[Файл:Hypergraph.jpg|right|thumb|Частный случай гипергафа, где <tex>E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}</tex>]] | + | [[Файл:Hypergraph.jpg]] |
| − | Стоит заметить, что обычный граф является частным случаем гиперграфа, где каждое ребро имеет мощность <tex>2</tex>.
| + | Частный случай гипергафа, где <tex>E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}</tex> |
| | | | |
| − | ==Определения== | + | ==Основные понятия гиперграфов== |
| | | | |
| − | Так как множество гиперребер может быть любой мощности, существуют несколько понятий '''подграфа''' гиперграфа, называемых '''подгиперграфами''', '''частичные гиперграфы''' и '''разрез гиперграфов'''. Пусть <tex>H = (X, E) </tex> - гиперграф содержащий множество вершин <tex>X = \{x_i | i \in I_v\}</tex> и множество ребер <tex>E = \{e_i | i \in I_e, e_i \subseteq X\}</tex>, где <tex>I_v</tex> и <tex>I_e</tex> множества индексов вершин и ребер соответсвенно.
| + | Пусть <tex>V</tex> - подмножество <tex>X</tex>. Множество '''частичных''' гиперребер, индуцированных множеством вершин <tex>V</tex> в <tex>H</tex>, называется |
| | | | |
| − | '''Подгиперграфом''' называют гиперграф с некоторым множеством удаленных вершин. Формально, подгиперграф <tex>H_a</tex> , индуцированный подмножеством <tex>A</tex> множества <tex> X </tex>, который определен как
<tex>H_a = (A, \{e_i \cap A| e_i \cap A \neq \emptyset \}).</tex>
| + | <tex>E' = \{ e' \mid e' = e \cap V, e \in E \} - \{ \emptyset \}</tex> |
| | | | |
| − | '''Частичным''' гипергафом называется гиперграф, с множеством удаленных ребер. Данное подмножество <tex>J \subset I_e </tex> множества индексов ребер, частичный граф сгенерирован с помощью <tex>J</tex>, т.е <tex>(X, \{ e_i | i \in J \}).</tex> | + | <tex>E'</tex> называется '''вершинно-порожденным''' множеством. С этого момента, будем рассматривать сокращенные гиперграфы(т.е. никакое гиперребро не содержится в другом). |
| | | | |
| − | Пусть дано множество <tex>A \subseteq X</tex>, разрезом гиперграфа называют такой '''частичный''' гиперграф <tex>
H \times A = (A, \{e_i | i \in I_e, e_i \subseteq A \}).</tex>
| + | Рассмотрим множество <tex> V \subset X</tex>. '''Подгиперграфом''' гиперграфа <tex>H</tex>, индуцированного множеством вершин <tex>V</tex>, наызывается такой гиперграф <tex>H[V] = (V, E')</tex> с множеством гиперребер <tex>E'</tex>, которое является множеством частичных гиперребер, индуцированных множеством вершин <tex>V</tex> в <tex>H</tex>. |
| | | | |
| − | '''Двойственным''' гиперграфом <tex>H</tex>* к <tex>H</tex> называют такой гиперграф, в котором поменяны местами вершины и ребра таким образом, что вершины определяются как <tex>\{e_i\}</tex> и ребра определяются как <tex>\{X_m\}</tex>, где <tex>X_m = \{ e_i | x_m \in e_i \}.</tex> | + | '''Путем''' между двумя гиперребрами <tex>e_i</tex> и <tex>e_j</tex> гиперграфа <tex>H</tex> называется последовательность гиперребер <tex>e_{u_1}, e_{u_2} \ldots e_{u_k},</tex>, таких что : |
| | | | |
| − | Когда операция равенства определена, как показано ниже, операция взятия '''двойственного''' гиперграфа выглядит следующим образом
<tex>(H^*)^* = H.</tex>
| + | 1)<tex>e_{u_1} = e_i </tex> и <tex>e_{u_k} = e_j</tex> |
| | | | |
| − | Связный граф <tex>G</tex> с тем же множеством вершин, что и у связного гиперграфа <tex>H</tex> называется «принимающим» графом для <tex>H</tex>, если каждое гиперребро <tex>H</tex> включает связный подграф в <tex>G</tex>. Для несвязного гиперграфа <tex>H</tex> , <tex>G</tex> является «принимающим», если существует биекция между связными компонентами <tex>G</tex> и <tex>H</tex> , так что каждая связная компонента <tex>G</tex>' графа <tex>G</tex> является принимающей для соответствующего <tex>H</tex>'.
| + | 2)<tex>\forall v: 1 \leq v \leq k-1, e_v \cap e_{v+1} \ne \emptyset</tex> |
| | | | |
| − | ==Изоморфность и эквивалентность==
| + | [[Файл:Connected_hypergraph.jpg]] |
| − | Гиперграф <tex>H = (X, E)</tex> изоморфен гиперграфу <tex>G = (Y, F)</tex> , записывается как <tex>H \simeq G</tex>, если существует биекция <tex>w</tex> : <tex>X</tex> -> <tex>Y</tex>
и перестановка <tex>\pi</tex> множества <tex>I</tex> такая, что <tex>w</tex><tex>(e_i)</tex> = <tex>f_{\pi(i)}</tex>
| + | рис.1 Связный гиперграф |
| − | Тогда биекция <tex>w</tex> называется изоморфизмом гиперграфов. Стоит отметить, что
| |
| − | <tex>H \simeq G</tex> тогда и только тогда, когда <tex>H^* \simeq G^*</tex>
| |
| | | | |
| − | Когда ребра гиперграфа явно помечены, то появляется дополнительное понятие '''сильного изоморфизима'''. Говорят, что <tex>H</tex> '''сильно изоморфен''' <tex>G</tex> , если перестановка является тождественной. Записывается как <tex>H \cong G</tex>. Стоит отметить, что все строго изоморфный графы изоморфны, но не наоборот.
| |
| | | | |
| − | Когда вершины гиперграфа явно помечены, то появляется понятие '''эквивалентности''', а также '''равенства'''. Говорят, что <tex>H</tex> эквивалентен <tex>G</tex>, записывается как <tex>H \equiv G</tex>, если изоморфизм <tex>w</tex> имеет следующие свойства
| + | Гиперграф <tex>H</tex> называется '''связным''' тогда и только тогда, когда существует путь между каждой парой гиперребер. |
| | | | |
| − | <tex>w(x_n) = y_n</tex> | + | Пусть <tex>E</tex> - связный, сокращенный набор гиперребер, <tex>e_1</tex> и <tex>e_2</tex> - элементы <tex>E</tex> и <tex>q = e_1 \cap e_2</tex>. <tex>q</tex> называется '''сочленением''' <tex>E</tex> , если его удаления из всех гиперребер <tex>E</tex> разрывает это множество. На рис.1 <tex>q = e_4 \cap e_6 = \{ x_{12}, x_{13}\}</tex> является сочленением <tex>E</tex>. |
| | | | |
| − | и | + | Гиперграф называется <tex>\alpha</tex> - ацикличным, если каждое множество частичных ребер является связными, сокращенным, индуцированным множеством вершин и не допускающее сочленения, является тривиальным(т.е. содержит только один элемент). |
| | | | |
| − | <tex>w(e_i) = f_{\pi(i)}</tex> | + | Гиперграф на рис.1 не является <tex>\alpha</tex> - ацикличным, так как множество частичных гиперребер <tex>\{\{ x_1, x_2, x_3, x_4\}, \{ x_1, x_2, x_5, x_6\}, \{ x_4, x_6, x_8\}\}</tex> является связным, уменьшенным, не тривиальным и не допускают сочленения. Напротив, гиперграф на рис.2 является <tex>\alpha</tex> - ацикличным. |
| | | | |
| − | Заметим, что <tex>H \equiv G</tex> если, и только если <tex>H^* \cong G^*</tex>.
| + | [[Файл:Acyclic.jpg]] |
| − | Если, кроме того, перестановка <tex>\pi</tex> тождественна, то говорят, что <tex>H</tex> равен <tex>G</tex>, и записывается как <tex>H = G</tex>. Стоит отметить, что при таком определении равенства, графы самодвойственны, т.е. <tex>(H^*)^* = H</tex>.
| + | рис.2 <tex>\alpha</tex> - ацикличный гиперграф |
| | | | |
| − | '''Автоморфизмом''' гиперграфа называется изоморфизм из множества вершин в них же, т.е. переобозначение вершин.
| + | Пусть дан гиперграф <tex>H = (X, E)</tex>. Циклом в <tex>H</tex> называется последовательность гиперребер <tex>(e_{i_1}, e_{i_2}, \ldots , e_{i_k})</tex> удовлетворяющим следующим свойствам: |
| | | | |
| − | Пример.
| + | <tex>e_{i_k} = e_{i_1}</tex> |
| | | | |
| − | Рассмотрим гиперграфы с ребрами
| + | <tex>\forall 2 \le j \le k - 2</tex> и <tex>\forall e \in E, (S_{j-1} \cup S_j \cup S_{j+1}) \ e \ne \emptyset </tex>, где <tex>S_j = e_{i_j} \cap e_{i_{j+1}}, \forall 1 \le j \le k - 1</tex> |
| − | | |
| − | | |
| − | <tex>H = \{ e_1 = \{ a, b \}, e_2 = \{ b, c\}, e_3 = \{ c, d \}, e_4 = \{d, a\}, e_5 = \{b, d \}, e_6 = \{a, c \}\}</tex> | |
| − | | |
| − | | |
| − | <tex>G = \{ f_1 = \{\alpha, \beta\}, f_2 = \{\beta,\gamma\}, f_3 = \{\gamma,\delta\}, f_4 = \{\delta,\alpha\},f_5=\{\alpha,\gamma\},f_6=\{\beta,\delta\}\}</tex>
| |
| − | | |
| − | | |
| − | Тогда, очевидно, <tex>H</tex> и <tex>G</tex> изоморфны(с <tex>w(a) = \alpha</tex>, и т.д.), но они не строго изоморфны. Так, например, в <tex>H</tex> вершина <tex>a</tex> содержится в ребрах <tex>1, 4</tex> и <tex>6</tex>, так что
| |
| − | | |
| − | <tex> e_1 \cap e_4 \cap e_6 = \{a\}</tex>
| |
| − | | |
| − | Однако в <tex>G</tex> не существует вершины, которая содержится в ребрах <tex> 1, 4</tex> и <tex>6</tex>:
| |
| − | | |
| − | <tex> f_1 \cap f_4 \cap f_6 = \emptyset </tex>
| |
| − | | |
| − | В этом примере <tex>H</tex> и <tex>G</tex> эквивалентны, <tex>H \equiv G</tex>, и двойственные строго изоморфны: <tex>H^* \cong G^*</tex>.
| |
| − | | |
| − | ==Ацикличность==
| |
| − | | |
| − | В отличие от обычных неориентированных графов, для которых существует только одно понятие ацикличности, существует множество неэквивалентных определений ацикличности гиперграфов.
| |
| − | | |
| − | Первое определение ацикличности для гиперграфов было дано Клаудом Бержем: гиперграф называется ацикличным по Бержу, если инцидентный ему граф ацикличный. Это определение достаточно ограничено. Например, если гиперграф имеет какую-то пару вершин <tex>v \ne v'</tex> и какую-то пару гиперребер <tex>f \ne f'</tex>, таких что <tex>v, v' \in f</tex> и <tex>v, v' \in f'</tex>, тогда имеет место цикл по Бержу. Цикличность по Бержу может быть найдена за линейное время с помощью исследования инцидентности гиперграфа.
| |
| − | | |
| − | Также мы можем определить более слабое определение ацикличности гиперграфа, называемое <tex>\alpha</tex> - ацикличность. Это понятие ацикличности эквивалентно определению гиперграфа, который является конформальным(т.е. каждая клика исходного графа покрыта каким-то гиперребром), и при этом исходный граф является хордальным ; это также эквивалентно сводимости пустого графа через GYO алгоритм(более известный как алгоритм Грэхема), повторяющийся процесс, который удаляет гиперребра с использованием главного определения "ухо графа". В области теории баз данных известно, что схема баз данных обладает некоторыми желательными свойствами, если ее основной граф является <tex>\alpha</tex> - ациклическим. <tex>\alpha</tex> - ацикличность гиперграфа также может быть найдена за линейное время.
| |
| − | | |
| − | Стоит отметить, что <tex>\alpha</tex> - ацикличность графа имеет некоторое нелогичное свойство, а именно, что при добавлении к <tex>\alpha</tex> - цикличному графу гиперребер гиперграф может стать <tex>\alpha</tex> - ацикличным. Например, добавление гиперребра, которое содержит все вершина гиперграфа, всегда будет давать <tex>\alpha</tex> - ацикличность графа. Частично мотивированным этим недостатком, Рональд Феджин определил более сильные понятия - <tex>\beta</tex> - ацикличность и <tex>\gamma</tex> - ацикличность. Можно констатировать <tex>\beta</tex> - ацикличность как требование, чтобы все подгиперграфы исходного гиперграфа были <tex>\alpha</tex> - ацикличными, что ээквивалентно выше упомянотому определению Грэхема. Понятие <tex>\gamma</tex> - ацикличности имеет более ограниченное определение, которое эквивалентно несколькими желательными свойствами схем баз данных и связана с диаграммами Бахмена. <tex<\beta</tex> - ацикличность и <tex>\gamma</tex> - ацикличность может быть найдена за полиномиальное время.
| |
| − | | |
| − | ==Матрица инцидентности==
| |
| − | | |
| − | Пусть <tex>V = \{ v_1, v_2, ... , v_n \},</tex> и <tex>E = \{ e_1, e_2, ..., e_m \}</tex>. Каждый гиперграф имеет <tex>n \times m</tex> инцидентную матрицу <tex>A = (a_{ij}) </tex>, где
| |
| − | | |
| − | <tex> a_{ij} = \left \{ | |
| − | \begin{array}{ll}
| |
| − | 1,& v_i \in e_j \\
| |
| − | 0,& otherwise
| |
| − | \end{array} | |
| − | \right.
| |
| − | </tex>
| |
| − | | |
| − | Транспонированная матрица <tex>A^t</tex> инцидентной матрицы определяет гиперграф <tex>H^* = (V^*, E^*)</tex> называемая двойственной к <tex>H</tex> , где <tex>V^*</tex> явялется <tex>m</tex>-ым элементом множества и <tex>E^*</tex> является <tex>n</tex>-ым элементом множества подмножества <tex>V^*</tex>. Для <tex>v^*_j \in V^*</tex> и <tex>e^*_i \in E^*, v^*_j \in e^*_i</tex> если, и только если <tex>a_{ij} = 1</tex>.
| |
| − | | |
| − | ==Симметричные гиперграфы==
| |
| − | | |
| − | '''Рангом''' <tex>r(H)</tex> гиперграфа <tex>H</tex> называется максимальная мощность любого из гиперребер в гиперграфе. Если все ребра имеют одинаковыую мощность <tex>k</tex> , тогда гиперграф называется однородным или <tex>k</tex> - однородным, или <tex>k</tex> - гиперграфом. Обычный граф является 2-однородным гиепрграфом.
| |
| − | | |
| − | Степенью <tex>d(v)</tex> вершины <tex>v</tex> называется число гиперребер, которые содержат <tex>v</tex>. <tex>H</tex> называется'''<tex>k</tex>- регулярным''', если каждая вершина имеет степень <tex>k</tex>.
| |
| − | | |
| − | Две вершины <tex>x</tex> и <tex>y</tex> гиперграфа <tex>H</tex> называются симметричными, если существует такой автоморфизм, что <tex>w(x) = y</tex>. Тва ребра <tex>e_i</tex> и <tex>e_j</tex> называются симметричными, если существет такой автоморфизм, что <tex>w(e_i) = e_j</tex>.
| |
| − | | |
| − | Гиперграф называется '''вершинно-транзитивным'''(или '''вершинно-симметричным'''), если все вершины симметричны. Точно так же, гиперграф называется '''реберно-транзитивным'''6 если все его ребра симметричны. Если гиперграф и вершинно-тразитивный, и реберно-транзитивный , тогда гиперграф называется '''транзитивным'''.
| |
| Определение: |
| Гиперграфом [math]H[/math] называют такую пару [math]H = (X, E)[/math] , где [math]X[/math] - множество вершин, а [math]E[/math] - семейство подмножеств X, называемых гиперребрами |
Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом.
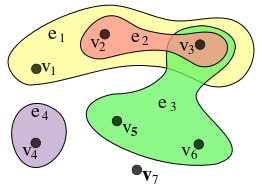 Частный случай гипергафа, где [math]E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}[/math]
Частный случай гипергафа, где [math]E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}[/math]
Основные понятия гиперграфов
Пусть [math]V[/math] - подмножество [math]X[/math]. Множество частичных гиперребер, индуцированных множеством вершин [math]V[/math] в [math]H[/math], называется
[math]E' = \{ e' \mid e' = e \cap V, e \in E \} - \{ \emptyset \}[/math]
[math]E'[/math] называется вершинно-порожденным множеством. С этого момента, будем рассматривать сокращенные гиперграфы(т.е. никакое гиперребро не содержится в другом).
Рассмотрим множество [math] V \subset X[/math]. Подгиперграфом гиперграфа [math]H[/math], индуцированного множеством вершин [math]V[/math], наызывается такой гиперграф [math]H[V] = (V, E')[/math] с множеством гиперребер [math]E'[/math], которое является множеством частичных гиперребер, индуцированных множеством вершин [math]V[/math] в [math]H[/math].
Путем между двумя гиперребрами [math]e_i[/math] и [math]e_j[/math] гиперграфа [math]H[/math] называется последовательность гиперребер [math]e_{u_1}, e_{u_2} \ldots e_{u_k},[/math], таких что :
1)[math]e_{u_1} = e_i [/math] и [math]e_{u_k} = e_j[/math]
2)[math]\forall v: 1 \leq v \leq k-1, e_v \cap e_{v+1} \ne \emptyset[/math]
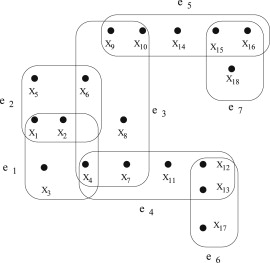 рис.1 Связный гиперграф
рис.1 Связный гиперграф
Гиперграф [math]H[/math] называется связным тогда и только тогда, когда существует путь между каждой парой гиперребер.
Пусть [math]E[/math] - связный, сокращенный набор гиперребер, [math]e_1[/math] и [math]e_2[/math] - элементы [math]E[/math] и [math]q = e_1 \cap e_2[/math]. [math]q[/math] называется сочленением [math]E[/math] , если его удаления из всех гиперребер [math]E[/math] разрывает это множество. На рис.1 [math]q = e_4 \cap e_6 = \{ x_{12}, x_{13}\}[/math] является сочленением [math]E[/math].
Гиперграф называется [math]\alpha[/math] - ацикличным, если каждое множество частичных ребер является связными, сокращенным, индуцированным множеством вершин и не допускающее сочленения, является тривиальным(т.е. содержит только один элемент).
Гиперграф на рис.1 не является [math]\alpha[/math] - ацикличным, так как множество частичных гиперребер [math]\{\{ x_1, x_2, x_3, x_4\}, \{ x_1, x_2, x_5, x_6\}, \{ x_4, x_6, x_8\}\}[/math] является связным, уменьшенным, не тривиальным и не допускают сочленения. Напротив, гиперграф на рис.2 является [math]\alpha[/math] - ацикличным.
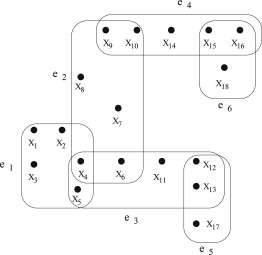 рис.2 [math]\alpha[/math] - ацикличный гиперграф
рис.2 [math]\alpha[/math] - ацикличный гиперграф
Пусть дан гиперграф [math]H = (X, E)[/math]. Циклом в [math]H[/math] называется последовательность гиперребер [math](e_{i_1}, e_{i_2}, \ldots , e_{i_k})[/math] удовлетворяющим следующим свойствам:
[math]e_{i_k} = e_{i_1}[/math]
[math]\forall 2 \le j \le k - 2[/math] и [math]\forall e \in E, (S_{j-1} \cup S_j \cup S_{j+1}) \ e \ne \emptyset [/math], где [math]S_j = e_{i_j} \cap e_{i_{j+1}}, \forall 1 \le j \le k - 1[/math]


