Гиперграфы — различия между версиями
Ivan (обсуждение | вклад) (sta) |
Ivan (обсуждение | вклад) (sta) |
||
| Строка 6: | Строка 6: | ||
Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом. | Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом. | ||
| − | [[Файл:Hypergraph.jpg]] | + | [[Файл:Hypergraph.jpg]] рис.1 |
Частный случай гипергафа, где <tex>E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}</tex> | Частный случай гипергафа, где <tex>E=\{e_1, e_2, e_3, e_4\} = \{\{v_1, v_2, v_3\}, \{v_2,v_3\}, \{v_3,v_5.v_6\}, \{v_4\}\}</tex> | ||
==Основные понятия гиперграфов== | ==Основные понятия гиперграфов== | ||
| − | + | {{Определение | |
| + | |definition= | ||
| + | '''Путем''' между двумя гиперребрами <tex>e_i</tex> и <tex>e_j</tex> гиперграфа <tex>H</tex> называется последовательность гиперребер <tex>e_{u_1}, e_{u_2} , \ldots ,e_{u_k}</tex>, таких что : | ||
| − | <tex> | + | 1) <tex>e_{u_1} = e_i </tex> и <tex>e_{u_k} = e_j</tex> |
| − | <tex> | + | 2) <tex>\forall v: 1 \leq v \leq k-1, e_v \cap e_{v+1} \ne \emptyset</tex> |
| + | }} | ||
| − | + | {{Определение | |
| + | |definition= | ||
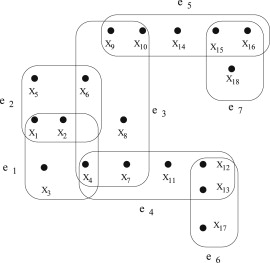
| + | Гиперграф <tex>H</tex> называется '''связным''' тогда и только тогда, когда существует путь между каждой парой гиперребер. | ||
| + | }} | ||
| + | |||
| + | [[Файл:Connected_hypergraph.jpg]] | ||
| + | рис.2 Связный гиперграф | ||
| + | |||
| + | Пусть <tex>E</tex> - связный, сокращенный набор гиперребер, <tex>e_1</tex> и <tex>e_2</tex> - элементы <tex>E</tex> и <tex>q = e_1 \cap e_2</tex>. | ||
| + | {{Определение | ||
| + | |definition= | ||
| + | <tex>q</tex> называется '''сочленением''' <tex>E</tex> , если при его удалении из всех гиперребер <tex>E</tex>, множество разрывается. | ||
| + | }} | ||
| + | |||
| + | На рис.2 <tex>q = e_4 \cap e_6 = \{ x_{12}, x_{13}\}</tex> является сочленением <tex>E</tex>. | ||
| + | |||
| + | ==Матрица инцидентности == | ||
| + | |||
| + | Пусть дан гиперграф <tex>H = (X, E)</tex> , где <tex> X = \{ x_1, x_2, \ldots , x_n \}</tex> и <tex> E = \{ e_1, e_2, \ldots , e_m \}</tex>. Любой гиперграф может задаваться матрицей инцидентности <tex>A = (a_{ij}) </tex> размером <tex> n \times m</tex>, где | ||
| − | + | <tex> a_{ij} = \left \{ | |
| + | \begin{array}{ll} | ||
| + | 0, & x_i \in e_j \\ | ||
| + | 1, & otherwise | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </tex> | ||
| − | 1 | + | Так например, для гиперграфа на рис.1 мы имеем такую матрицу инцидентности |
| − | |||
| − | + | <tex> A = </tex> | |
| − | + | <tex>\begin{pmatrix} | |
| + | 1 & 0 & 0 & 0\\ | ||
| + | 1 & 1 & 0 & 0\\ | ||
| + | 1 & 1 & 1 & 0\\ | ||
| + | 0 & 0 & 0 & 1\\ | ||
| + | 0 & 0 & 1 & 0\\ | ||
| + | 0 & 0 & 1 & 0\\ | ||
| + | 0 & 0 & 0 & 0\\ | ||
| + | \end{pmatrix}</tex> | ||
| + | |||
| + | ==Ацикличность гиперграфа== | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Циклом в <tex>H = (X, E)</tex> называется последовательность гиперребер <tex>(e_{i_1}, e_{i_2}, \ldots , e_{i_k})</tex> удовлетворяющим следующим свойствам: | ||
| + | |||
| + | 1) <tex>e_{i_k} = e_{i_1}</tex> | ||
| + | |||
| + | 2) <tex>\forall 2 \le j \le k - 2</tex> выполняется <tex>\forall e \in E : (S_{j-1} \cup S_j \cup S_{j+1}) \setminus e \ne \emptyset </tex>, где <tex>S_j = e_{i_j} \cap e_{i_{j+1}}</tex> для которых выполняется <tex>\forall 1 \le j \le k - 1</tex> | ||
| + | }} | ||
| + | |||
| + | Для определения ацикличного гиперграфа введем определение '''уха''' гиперграфа, а также редукцию GYO(Graham-Yu-Ozsoyoglu). | ||
| + | |||
| + | {{Определение | ||
| + | |definition= | ||
| + | Ухом(по англ. ear) гиперграфа называется такое гиперребро <tex>e</tex>, что его вершины можно разделить на две группы: | ||
| + | 1) Вершины, которые принадлежат только гиперребру <tex>e</tex> и никакому более. | ||
| − | + | 2) Вершины, которые принадлежат другим гиперребрам. | |
| + | }} | ||
| − | + | {{Определение | |
| + | |definition= | ||
| + | Определение редукции GYO содержит всего два шага: | ||
| − | + | 1) Устранение вершин, которые содержатся только в одном гиперребре. | |
| − | + | 2) Удаление гиперребер, которые содержатся в других. | |
| + | }} | ||
| − | + | То есть, мы удаляем вершины которые содержатся в ухе, и ни в каком более гиперребре. Затем удаляем гиперребра, оставляя другие вершины. | |
| − | |||
| − | + | {{Утверждение | |
| + | |statement= | ||
| + | Если гиперграф сводится к пустому с помощью редукции GYO, тогда он ацикличный. | ||
| + | }} | ||
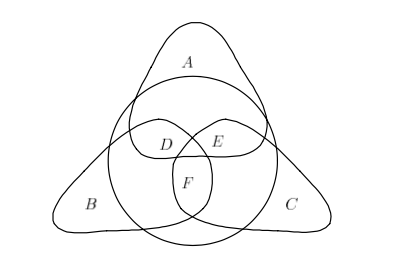
| − | + | [[Файл:Acyclic_hyper.png]] | |
| + | рис.3 Ацикличный гиперграф | ||
| − | + | С помощью редукции GYO удаляются вершины A, B и C (т.к они содержатся только в одном своем гиперребре), а затем удаляем оставшиеся внутренние гиперребра. | |
Версия 15:49, 3 января 2017
| Определение: |
| Гиперграфом называют такую пару , где - множество вершин, а - семейство подмножеств X, называемых гиперребрами |
Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом.
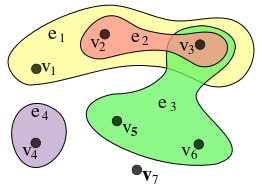 рис.1
Частный случай гипергафа, где
рис.1
Частный случай гипергафа, где
Основные понятия гиперграфов
| Определение: |
| Путем между двумя гиперребрами и гиперграфа называется последовательность гиперребер , таких что :
1) и 2) |
| Определение: |
| Гиперграф называется связным тогда и только тогда, когда существует путь между каждой парой гиперребер. |
Пусть - связный, сокращенный набор гиперребер, и - элементы и .
| Определение: |
| называется сочленением , если при его удалении из всех гиперребер , множество разрывается. |
На рис.2 является сочленением .
Матрица инцидентности
Пусть дан гиперграф , где и . Любой гиперграф может задаваться матрицей инцидентности размером , где
Так например, для гиперграфа на рис.1 мы имеем такую матрицу инцидентности
Ацикличность гиперграфа
| Определение: |
| Циклом в называется последовательность гиперребер удовлетворяющим следующим свойствам:
1) 2) выполняется , где для которых выполняется |
Для определения ацикличного гиперграфа введем определение уха гиперграфа, а также редукцию GYO(Graham-Yu-Ozsoyoglu).
| Определение: |
| Ухом(по англ. ear) гиперграфа называется такое гиперребро , что его вершины можно разделить на две группы:
1) Вершины, которые принадлежат только гиперребру и никакому более. 2) Вершины, которые принадлежат другим гиперребрам. |
| Определение: |
| Определение редукции GYO содержит всего два шага:
1) Устранение вершин, которые содержатся только в одном гиперребре. 2) Удаление гиперребер, которые содержатся в других. |
То есть, мы удаляем вершины которые содержатся в ухе, и ни в каком более гиперребре. Затем удаляем гиперребра, оставляя другие вершины.
| Утверждение: |
Если гиперграф сводится к пустому с помощью редукции GYO, тогда он ацикличный. |
С помощью редукции GYO удаляются вершины A, B и C (т.к они содержатся только в одном своем гиперребре), а затем удаляем оставшиеся внутренние гиперребра.