Разрез в планарных графах — различия между версиями
Evarand (обсуждение | вклад) (Алгоритм за O(n^2 logn)) |
Evarand (обсуждение | вклад) (рефакторинг) |
||
| Строка 1: | Строка 1: | ||
| − | Особенности [[укладка графа на плоскости | планарных графов]] позволяют реализовать поиск [[разрез, лемма о потоке через разрез | минимального разреза]] в планарном графе с лучшей асимптотикой, чем в произвольном графе. Лучший известный алгоритм работает с асимптотикой <math>O( | + | Особенности [[укладка графа на плоскости | планарных графов]] позволяют реализовать поиск [[разрез, лемма о потоке через разрез | минимального разреза]] в планарном графе с лучшей асимптотикой, чем в произвольном графе, где поиск минимального разреза требует поиска максимального потока, то есть работает за <math>O(V^2E)</math>. Лучший известный алгоритм для планарных графов работает с асимптотикой <math>O(V\log V)</math>. |
==Алгоритм за <math>O(n^2 \log n)</math>== | ==Алгоритм за <math>O(n^2 \log n)</math>== | ||
| − | Рассмотрим неориентированный граф <math>G=(V, E)</math>. Будем считать его трёхсвязным, если это не так, [[ | + | |
| + | ===Идея алгоритма=== | ||
| + | Рассмотрим граф <math>G^d</math>, [[двойственный граф планарного графа | двойственный]] данному графу <math>G</math>. Рассмотрим кратчайший путь <math>\Pi</math> между вершинами <math>\xi^s</math> и <math>\xi^t</math>, принадлежащими граням <math>\varphi_s</math> и <math>\varphi_t</math>, соответствующим вершинам <math>s</math> и <math>t</math> в исходном графе. Определим <math>\Pi</math>-левые и <math>\Pi</math>-правые ребра, <math>\Pi</math>-левые будут лежать "слева" по пути из <math>\xi^s</math> в <math>\xi^t</math>, а <math>\Pi</math>-"правые" справа. Формальное определение будет дано в следующем разделе. Тогда минимальный цикл в <math>G^d</math>, ограничивающий <math>\varphi_t</math>, будет <math>\xi_i</math>-циклом {{---}} циклом, содержащим ровно одно <math>\Pi</math>-левое и одно <math>\Pi</math>-правое ребро, причем <math>\Pi</math>-левое ребро входит в вершину <math>\xi_i</math>. | ||
| + | |||
| + | [[Файл:Xi_cycles.png|600px|thumb|center|Кси-циклы]] | ||
| + | |||
| + | Каждый такой цикл соответствует разрезу в <math>G</math>. Тогда алгоритм можно записать так: | ||
| + | # Построим граф <math>G^d</math>, двойственный исходному графу <math>G</math> | ||
| + | # Найдем кратчайший путь <math>\Pi</math> между вершинами <math>\xi^s</math> и <math>\xi^t</math> | ||
| + | # Для каждой вершины <math>\xi_i\in\Pi</math> найдем кратчайший <math>\xi_i</math>-цикл | ||
| + | # Найдем среди этих циклов цикл минимальной длины и построим соответствующий ему разрез в <math>G</math> | ||
| + | |||
| + | ===Корректность и асимптотика=== | ||
| + | Рассмотрим неориентированный граф <math>G=(V, E)</math>. Будем считать его трёхсвязным, если это не так, [[триангуляция полигонов (ушная + монотонная) | триангулируем]] его, используя ребра нулевой пропускной способности, это не изменит значение минимального <math>(s-t)-</math> разреза. Минимальный разрез исходного графа будет состоять из ребер минимального разреза нового графа, которые есть и в исходном графе. | ||
<math>G</math> трёхсвязен, поэтому существует единственный [[двойственный граф планарного графа | двойственный]] ему граф <math>G^d=(X, A)</math>, при этом <math>G^d</math> также трёхсвязен. Будем обозначать множество граней <math>G</math> как <math>F</math>, множество граней <math>G^d</math> как <math>\Phi</math>. Между элементами каждой из пар множеств <math>V-\Phi</math>, <math>E-A</math> и <math>F-X</math> существует взаимно однозначное соответствие. Будем обозначать как <math>\alpha^d\in E</math> элемент, соответствующий <math>\alpha\in A</math>. Тогда длину ребра <math>\alpha</math> определим как <math>l(\alpha)=c(\alpha^d)</math>. | <math>G</math> трёхсвязен, поэтому существует единственный [[двойственный граф планарного графа | двойственный]] ему граф <math>G^d=(X, A)</math>, при этом <math>G^d</math> также трёхсвязен. Будем обозначать множество граней <math>G</math> как <math>F</math>, множество граней <math>G^d</math> как <math>\Phi</math>. Между элементами каждой из пар множеств <math>V-\Phi</math>, <math>E-A</math> и <math>F-X</math> существует взаимно однозначное соответствие. Будем обозначать как <math>\alpha^d\in E</math> элемент, соответствующий <math>\alpha\in A</math>. Тогда длину ребра <math>\alpha</math> определим как <math>l(\alpha)=c(\alpha^d)</math>. | ||
| Строка 10: | Строка 23: | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | <math>C</math> {{---}} минимальный <math>(s-t)-</math> разрез, тогда <math>C^d=\{\alpha | + | <math>C</math> {{---}} минимальный <math>(s-t)-</math> разрез, тогда <math>C^d=\{\alpha \mid \alpha^d\in C\}</math> {{---}} цикл минимальной длины, ограничивающий <math>\varphi_t</math>. |
| + | Формальное доказательство леммы громоздкое и здесь приведено не будет, однако сама лемма достаточно интуитивно понятна.<ref>"The following lemma is intuitive; however its formal proof is tedious, and therefore, omitted.", Maximum flow in planar networks, Itai & Shiloach, 1979</ref> | ||
}} | }} | ||
| − | + | Пусть <math>\xi^s\in\varphi_s</math>, <math>\xi^t\in\varphi_t</math>, <math>\Pi=(\xi^s=\xi_1, \ldots, \xi_k=\xi^t)</math> {{---}} кратчайший путь между <math>\xi^s</math> и <math>\xi^t</math> в <math>G^d</math>, <math>\alpha_i</math> {{---}} ребро между <math>\xi_{i-1}</math> и <math>\xi_i</math> для <math>i=2,\ldots,k</math>. Будем называть ребро <math>\xi-\xi_i\in A</math> <math>\Pi</math>-левым, если оно находится между <math>\alpha_i</math> и <math>\alpha_{i+1}</math> при обходе ребер, входящих в <math>\xi_i</math>, по часовой стрелке от <math>\alpha_i</math>, и <math>\Pi</math>-правым, если оно находится между <math>\alpha_{i+1}</math> и <math>\alpha_i</math>. | |
| + | Для того, чтобы это определение имело смысл для первой и последней вершин пути, можно добавить две вершины <math>\xi_0</math> и <math>\xi_{k+1}</math> и два ребра <math>\alpha_1=\xi_0-\xi_1</math> и <math>\alpha_{k+1}=\xi_k-\xi_{k+1}</math>. Важно, что никакое ребро не является одновременно <math>\Pi</math>-левым и <math>\Pi</math>-правым. | ||
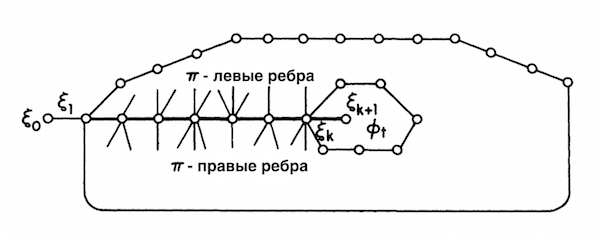
| − | + | [[Файл:Виды_ребер.png|600px|thumb|center|П-левые и П-правые ребра]] | |
| − | |||
| − | Будем называть <math>\xi_i</math> - циклом простой цикл, который содержит ровно одно <math>\Pi | + | Будем называть <math>\xi_i</math>-циклом простой цикл, который содержит ровно одно <math>\Pi</math>-левое и одно <math>\Pi</math>-правое ребро, при этом <math>\Pi</math>-левое ребро входит в вершину <math>\xi_i</math>. Любой <math>\xi_i</math>-цикл ограничивает <math>\varphi_t</math>. |
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Пусть <math>C</math> {{---}} кратчайший ограничивающий <math>\varphi_t</math> цикл. Тогда существует <math>\xi_i</math> - цикл такой же длины. | + | Пусть <math>C</math> {{---}} кратчайший ограничивающий <math>\varphi_t</math> цикл. Тогда существует <math>\xi_i</math>-цикл такой же длины. |
|proof= | |proof= | ||
| − | <math>\Pi</math> {{---}} кратчайший путь между <math>\xi^s</math> и <math>\xi^t</math>, поэтому любой содержащийся в <math>\Pi</math> путь между <math>\xi_i</math> и <math>\xi_j</math> также кратчайший. При этом любой ограничиващий <math>\varphi_t</math> цикл обязан пересекать <math>\Pi</math>. Цикл, не являющийся <math>\xi_i</math> - циклом, не будет кратчайшим, так как его можно будет сократить вдоль пути <math>\Pi</math>. | + | <math>\Pi</math> {{---}} кратчайший путь между <math>\xi^s</math> и <math>\xi^t</math>, поэтому любой содержащийся в <math>\Pi</math> путь между <math>\xi_i</math> и <math>\xi_j</math> также кратчайший. При этом любой ограничиващий <math>\varphi_t</math> цикл обязан пересекать <math>\Pi</math>. Цикл, не являющийся <math>\xi_i</math>-циклом, не будет кратчайшим, так как его можно будет сократить вдоль пути <math>\Pi</math>. |
}} | }} | ||
| − | + | Для поиска минимального <math>\xi_i</math>-цикла построим из неориентированного графа <math>G</math> ориентированный граф <math>\vec{G}^d</math> следующим образом: все <math>\Pi</math>-левые ребра ориентируем из вершин <math>\xi\in\Pi</math>, все <math>\Pi</math>-правые ребра ориентируем в вершины <math>\xi\in\Pi</math>, а остальные ребра <math>u\leftrightarrow v</math> заменим на два ребра <math>u\rightarrow v</math> и <math>v\rightarrow u</math>. | |
| − | |||
| − | |||
| − | |||
| − | Для поиска минимального <math>\xi_i</math> - цикла построим из неориентированного графа <math>G</math> ориентированный граф <math>\vec{G}^d</math> следующим образом: все <math>\Pi | ||
{{Лемма | {{Лемма | ||
|statement= | |statement= | ||
| − | Пусть <math>\xi_i\in\Pi</math>, <math>P_i</math> {{---}} кратчайший нетривиальный путь из <math>\xi_i</math> в <math>\xi_i</math> в <math>\vec{G}^d</math>. Тогда соответствующий путь в <math>G^d</math> является кратчайшим <math>\xi_i</math> - циклом. | + | Пусть <math>\xi_i\in\Pi</math>, <math>P_i</math> {{---}} кратчайший нетривиальный путь из <math>\xi_i</math> в <math>\xi_i</math> в <math>\vec{G}^d</math>. Тогда соответствующий путь в <math>G^d</math> является кратчайшим <math>\xi_i</math>-циклом. |
|proof= | |proof= | ||
| − | Из определения <math>\vec{G}^d</math> следует, что если нетривиальный путь из <math>\xi_i</math> в <math>\xi_i</math> содержит больше одного <math>\Pi | + | Из определения <math>\vec{G}^d</math> следует, что если нетривиальный путь из <math>\xi_i</math> в <math>\xi_i</math> содержит больше одного <math>\Pi</math>-правого или <math>\Pi</math>-левого ребра, то в нем есть самопересечение, то есть он не является простым, следовательно, не является кратчайшим <math>\xi_i</math>-циклом. |
}} | }} | ||
| − | Таким образом, нахождение минимального <math>\xi_i</math> - цикла эквивалентно нахождению кратчайшего нетривиального пути из <math>\xi_i</math> в <math>\xi_i</math> в <math>\vec{G}^d</math>. Это можно сделать за <math>O(m\log n)</math>, например, с помощью [[алгоритм Дейкстры | алгоритма Дейкстры]]. Так как в планарных графах <math>m=O(n)</math>, это равно <math>O(n\log n)</math>. Максимум <math>n</math> таких поисков дадут итоговую асимптотику <math>O(n^2\log n)</math>. | + | Таким образом, нахождение минимального <math>\xi_i</math>-цикла эквивалентно нахождению кратчайшего нетривиального пути из <math>\xi_i</math> в <math>\xi_i</math> в <math>\vec{G}^d</math>. Это можно сделать за <math>O(m\log n)</math>, например, с помощью [[алгоритм Дейкстры | алгоритма Дейкстры]]. Так как в планарных графах <math>m=O(n)</math>, это равно <math>O(n\log n)</math>. Максимум <math>n</math> таких поисков дадут итоговую асимптотику <math>O(n^2\log n)</math>. |
==См. также== | ==См. также== | ||
| Строка 46: | Строка 56: | ||
* [[Разрез, лемма о потоке через разрез]] | * [[Разрез, лемма о потоке через разрез]] | ||
* [[Укладка графа на плоскости]] | * [[Укладка графа на плоскости]] | ||
| + | |||
| + | ==Примечания== | ||
| + | <references/> | ||
==Источники информации== | ==Источники информации== | ||
| − | * [http://verona.dei.unipd.it/~prin08/primo_meeting/italiano.pdf | + | * [http://verona.dei.unipd.it/~prin08/primo_meeting/italiano.pdf Improved Algorithms for Min Cuts and Max Flows in Undirected Planar Graphs] |
| − | * [https://pdfs.semanticscholar.org/b838/35db99723f922b7b286d10952b08c68970a7.pdf | + | * [https://pdfs.semanticscholar.org/b838/35db99723f922b7b286d10952b08c68970a7.pdf Maximum flow in planar networks, Itai & Shiloach, 1979] |
[[Категория: Алгоритмы и структуры данных]] | [[Категория: Алгоритмы и структуры данных]] | ||
[[Категория: Укладки графов]] | [[Категория: Укладки графов]] | ||
Версия 00:26, 6 января 2017
Особенности планарных графов позволяют реализовать поиск минимального разреза в планарном графе с лучшей асимптотикой, чем в произвольном графе, где поиск минимального разреза требует поиска максимального потока, то есть работает за . Лучший известный алгоритм для планарных графов работает с асимптотикой .
Содержание
Алгоритм за
Идея алгоритма
Рассмотрим граф , двойственный данному графу . Рассмотрим кратчайший путь между вершинами и , принадлежащими граням и , соответствующим вершинам и в исходном графе. Определим -левые и -правые ребра, -левые будут лежать "слева" по пути из в , а -"правые" справа. Формальное определение будет дано в следующем разделе. Тогда минимальный цикл в , ограничивающий , будет -циклом — циклом, содержащим ровно одно -левое и одно -правое ребро, причем -левое ребро входит в вершину .
Каждый такой цикл соответствует разрезу в . Тогда алгоритм можно записать так:
- Построим граф , двойственный исходному графу
- Найдем кратчайший путь между вершинами и
- Для каждой вершины найдем кратчайший -цикл
- Найдем среди этих циклов цикл минимальной длины и построим соответствующий ему разрез в
Корректность и асимптотика
Рассмотрим неориентированный граф . Будем считать его трёхсвязным, если это не так, триангулируем его, используя ребра нулевой пропускной способности, это не изменит значение минимального разреза. Минимальный разрез исходного графа будет состоять из ребер минимального разреза нового графа, которые есть и в исходном графе.
трёхсвязен, поэтому существует единственный двойственный ему граф , при этом также трёхсвязен. Будем обозначать множество граней как , множество граней как . Между элементами каждой из пар множеств , и существует взаимно однозначное соответствие. Будем обозначать как элемент, соответствующий . Тогда длину ребра определим как .
Будем обозначать грани , соответствующие вершинам и , как и соответственно. Далее будем считать, что — внешняя грань .
| Лемма: |
— минимальный разрез, тогда — цикл минимальной длины, ограничивающий .
Формальное доказательство леммы громоздкое и здесь приведено не будет, однако сама лемма достаточно интуитивно понятна.[1] |
Пусть , , — кратчайший путь между и в , — ребро между и для . Будем называть ребро -левым, если оно находится между и при обходе ребер, входящих в , по часовой стрелке от , и -правым, если оно находится между и . Для того, чтобы это определение имело смысл для первой и последней вершин пути, можно добавить две вершины и и два ребра и . Важно, что никакое ребро не является одновременно -левым и -правым.
Будем называть -циклом простой цикл, который содержит ровно одно -левое и одно -правое ребро, при этом -левое ребро входит в вершину . Любой -цикл ограничивает .
| Лемма: |
Пусть — кратчайший ограничивающий цикл. Тогда существует -цикл такой же длины. |
| Доказательство: |
| — кратчайший путь между и , поэтому любой содержащийся в путь между и также кратчайший. При этом любой ограничиващий цикл обязан пересекать . Цикл, не являющийся -циклом, не будет кратчайшим, так как его можно будет сократить вдоль пути . |
Для поиска минимального -цикла построим из неориентированного графа ориентированный граф следующим образом: все -левые ребра ориентируем из вершин , все -правые ребра ориентируем в вершины , а остальные ребра заменим на два ребра и .
| Лемма: |
Пусть , — кратчайший нетривиальный путь из в в . Тогда соответствующий путь в является кратчайшим -циклом. |
| Доказательство: |
| Из определения следует, что если нетривиальный путь из в содержит больше одного -правого или -левого ребра, то в нем есть самопересечение, то есть он не является простым, следовательно, не является кратчайшим -циклом. |
Таким образом, нахождение минимального -цикла эквивалентно нахождению кратчайшего нетривиального пути из в в . Это можно сделать за , например, с помощью алгоритма Дейкстры. Так как в планарных графах , это равно . Максимум таких поисков дадут итоговую асимптотику .
См. также
Примечания
- ↑ "The following lemma is intuitive; however its formal proof is tedious, and therefore, omitted.", Maximum flow in planar networks, Itai & Shiloach, 1979