Минимально узкое остовное дерево

Минимально узкое остовное дерево (англ. Minimum bottleneck spanning tree, MBST) в связанном взвешенном неориентированном графе [math]-[/math] это остовное дерево графа, у которого максимальное ребро минимально. Узким ребром в графе назовём максимальное по весу. Остовное дерево является минимально узким, если в графе нет остовного дерева с меньшим узким ребром.

Задача MBST и минимальное остовное дерево

Утверждение:

Минимальное остовное дерево является minimum bottleneck spanning tree.

[math]\triangleright[/math]

Предположим, если минимальное остовное не является MBST, значит в графе существует набор ребер которые мы не взяли в наш остов, при замене на которые, наше дерево станет MBST. Так же рёбра вне остова должны быть меньше рёбер из остова, чтобы уменьшить минимальное максимально ребро. Но по определению MST, сумма рёбер дерева минимальна, значит вне остова нету рёбер с меньшим весом. Так как наше предположение неверно, MST является MBST.

[math]\triangleleft[/math]

Утверждение:

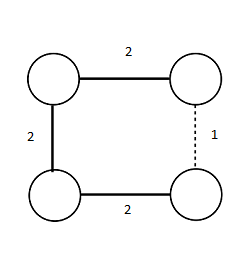
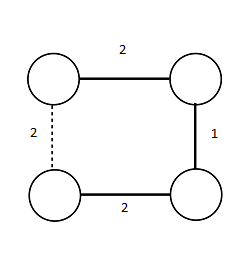
Minimum bottleneck spanning tree не всегда является минимальным остовным деревом.

[math]\triangleright[/math]

Рассмотрим пример, где MBST не является минимальным остовным деревом: Пример MBST дерева. Пример MST дерева.

[math]\triangleleft[/math]

Является ли остовное дерево MBST

Задача:

Проверка остовного дерева на MBST.

Алгоритм

Если у нас получится соединить все вершины графа, используя рёбра меньше максимального из нашего остова, значит мы сможем построить другой остов, в котором максимальное ребро меньше нашего максимального. Для этого найдём максимальное ребро в нашем дереве. Соединим все вершины, между которыми рёбра с весом меньше максимального при помощи СНМ. Если в результате у нас все вершины лежат в одном множестве, значит наше дерево не является MBST, иначе оно MBST.

Асимптотика

Максимальное ребро мы ищем линейно за количество рёбер в дереве [math]O(N)[/math].
Работа с СНМ займет [math]O(N\alpha(V))[/math], где [math]\alpha[/math] — обратная функция Аккермана, которая не превосходит [math]4[/math] во всех практических приложениях и которую можно принять за константу.
В результате получаем алгоритм работающий за линейное время [math]O(N)[/math].

Псевдокод

  function ifMBST():
     int united = 0, maxEdge = -Inf
     for i = 1 to tree.size
        maxEdge = max(maxEdge, tree[i].cost)
     for i = 1 to n
        if e[i].cost >= maxEdge
           continue
        if find(e[i].from]) != find(e[i].to)
           united++
        unite(e[i].from,e[i].to)
     if united == e.size - 1
        return true
     else 
        return false

Cм. также

• Алгоритм Краскала
• Остовные деревья: определения, лемма о безопасном ребре
• СНМ (наивные реализации)

Источники информации

• Википедия — Minimum bottleneck spanning tree