Convex hull trick

Convex hull - выпуклая оболочка; Convex hull trick - один из методов оптимизации динамического программирования, использующий идею выпуклой оболочки. Позволяет улучшить ассимптотику решения некоторых задач, решемых методом динамического программирования с [math]O(n^2)[/math] до [math]O(n*logn)[/math]. Техника впервые появилась в 1995 году (задачу на нее предложили в USACO - национальной олимпиаде США по программированию). Массовую известность получила после IOI (международной олимпиады по программированию для школьников) 2002

Пример задачи, решаемой методом convex hull trick

Рассмотрим задачу на ДП:

Задача:

Есть n деревьев с высотами [math]a1, a2, \dots an[/math] (в метрах). Требуется спилить их все, потратив минимальное количество монет на заправку бензопилы. Но пила устроена так, что она может спиливать только по 1 метру от дерева, к которому ее применили. Также после срубленного метра (любого дерева) пилу нужно заправлять, платя за бензин определенной кол-во монет. Причем стоимость бензина зависит от срубленных (полностью) деревьев. Если сейчас максимальный индекс срубленного дерева равен i, то цена заправки равна ci. Изначально пила заправлена. Также известны следующие ограничения : [math]c[n] = 0, a[1] = 1, a[i][/math] возрастают, [math]c[i][/math] убывают. Изначально пила заправлена. (убывание и возрастание нестрогие)

(Задача H с Санкт-Петербургских сборов к РОИ [1])

Наивное решение

Сначала заметим важный факт : т.к. [math]c[i][/math] убывают (нестрого) и [math]c[n] = 0[/math], то все [math]c[i][/math] неотрицательны. Понятно, что нужно затратив минимальную стоимость срубить последнее ([math]n[/math]-е) дерево, т.к. после него все деревья можно будет рубить бесплатно (т.к. [math]c[n] = 0[/math]). Посчитаем следующую динамику : [math]dp[i][/math] - минимальная стоимость, заплатив которую можно добиться того, что дерево номер [math]i.[/math] будет срублено. База динамики : [math]dp[1] = 0[/math], т.к. изначально пила заправлена и высота первого дерева равна 1, по условию задачи. Переход динамики : понятно, что выгодно рубить сначала более дорогие и низкие деревья, а потом более высокие и дешевые (док-во этого факта оставляется читателям как несложное упражнение, т.к. эта идея относится скорее к теме жадных алгоритмнов, чем к теме данной статьи). Поэтому перед [math]i[/math]-м деревом мы обязательно срубили какое-то [math]j[/math]-е, причем [math]j \lt i[/math]. Поэтому чтобы найти [math]dp[i][/math] нужно перебрать все [math]1 \leqslant j \lt i[/math] и попытаться использовать ответ для дерева намер [math]j[/math]. Итак, пусть перед [math]i[/math]-м деревом мы полностью срубили [math]j[/math]-е, причем высота [math]i[/math]-го дерева составляет [math]a[i][/math], а т.к. последнее дерево, которое мы срубили имеет индекс [math]j[/math], то стоимость каждого метра [math]i[/math]-го дерева составит [math]c[j][/math]. Поэтому на сруб [math]i[/math]-го дерева мы потратим [math]a[i] * c[j][/math] монет. Также не стоит забывать, ситуацию, когда [math]j[/math]-е дерево полностью срублено, мы получили не бесплатно, а за [math]dp[j][/math] монет. Итогвая формула пересчета : [math]dp[i] = \min__{j=1...i-1} (dp[j] + a[i] * c[j])[/math].

Посмотрим на код выше описанного решения:

int simple-dp(int a[], int c[], int n)
dp[1] = 0
dp[2] = dp[3] = ... = dp[n] = [math]\infty[/math]
for  i = 1..n-1  {
   dp[i] = +[math]\infty[/math]
   for j = 0..i-1 {
       if (dp[j] + a[i] * c[j] < dp[i])
           dp[i] = dp[j] + a[i] * c[j]
           }
}
return dp[n]

Нетрудно видеть, что такая динамика работает за [math]O(n^2)[/math].

Ключевая идея оптимизации

1) Сделаем замену обозначений. Давайте обозначим [math]dp[j][/math] за [math]b[j][/math], [math]a[i][/math] за [math]x[i][/math], а [math]c[j][/math] за [math]k[j][/math].

2) Теперь формула приняла вид [math]dp[i] = min_{j=0...i-1}(k[j]*x[i] + b[j])[/math]. Выражение [math]k[j]*x + b[j][/math] - это в точности уравнение прямой вида [math]y = kx + b[/math].

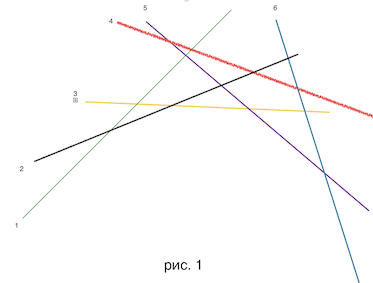
3) Сопоставим каждому [math]j[/math], обработанному ранее, прямую [math]y[j](x) = k[j]*x + b[j][/math]. Из условия «[math]c[i][/math] убывают [math]\lt =\gt k[j][/math] уменьшаются с номером [math]j[/math]» следует то, что прямые, полученные ранее отсортированы в порядке убывания углового коэффициент. Давайте нарисуем несколько таких прямых :

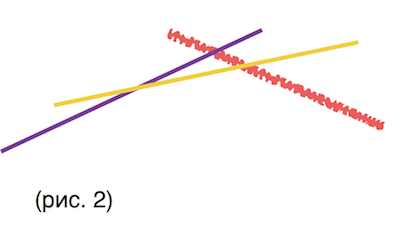
4) Выделим множество точек [math](x0, y0)[/math] , таких что все они принадлежат одной из прямых и при этом нету ни одной прямой [math]y’(x)[/math], такой что [math]y’(x0) \lt y0[/math]. Иными словами возьмем «выпуклую (вверх) оболочку» нашего множества прямых (её еще называют нижней ошибающей множества прямых на плоскости). Назовем ее «[math]y = convex(x)[/math]». Видно, что множество точек (x, convex(x)) представляет собой выпуклую вверх функцию.

Для чего нужна нижняя огибающая множества прямых

Пусть мы считаем динамику для [math]i[/math]-го дерева. Его задает [math]x[i][/math]. Итак, нам нужно для данного [math]x[i][/math] найти [math]min_{j=0..i-1}(k[j]*x[i] + b[i]) = min_{j=0..i-1}(y[j](x[i]))[/math]. Это выражение есть convex(x[i]). Из монотонности угловых коэффицентов отрезков, задающих выпуклую оболочку, и их расположения по координаты x следует то, что отрезок, который пересекает прямую [math]x = x[i][/math], можно найти бинарным поиском. Это потребует [math]O(logn)[/math] времени на поиск такого j, что dp[i] = k[j] * x[i] + b[j]. Теперь осталось научиться поддерживать множество прямых и быстро добавлять [math]i[/math]-ю прямую после того, как мы посчитали [math]b[i] = dp[i][/math].

Воспользуемся идеей алгоритма построения выпуклой оболочки множества точек. Заведем 2 стека [math]k[][/math] и [math]b[][/math], которые задают прямые в отсортированном порядке их угловыми коэффицентами и свободными членами. Рассмотрим ситуацию, когда мы хотим добавить новую ([math]i[/math]-тую) прямую в множество. Пусть сейчас в множестве лежит [math]sz[/math] прямых (нумерация с 1). Пусть [math](xL, yL)[/math] - точка пересечения [math]sz - 1[/math]-й прямой множества и [math]sz[/math]-й, а [math](xR, yR)[/math] - точка пересечения новой прямой, которую мы хотим добавить в конец множества и [math]sz[/math]-й. Нас будут интересовать только их [math]x[/math]-овые координаты [math]xL[/math] и [math]xR[/math], соответственно. Если оказалось, что новая прямая пересекает [math]sz[/math]-ю прямую выпуклой оболочки позже, чем [math]sz[/math]-я [math]sz - 1[/math]-ю, т.е. [math](xL \gt = xR)[/math], то [math]sz[/math]-ю удалим из нашего множества, иначе - остановимся. Так будем делать, пока либо кол-во прямых в стеке не станет равным 2, либо [math]xL[/math] не станет меньше [math]xR.[/math]

Асимптотика : аналогично обычному алгоритму построения выпуклой оболочки, каждая прямая ровно 1 раз добавится в стек и максимум 1 раз удалится. Значит время работы перестройки выпуклой оболочки займет [math]O(n)[/math] суммарно.

Корректность : достаточно показать, что последнюю прямую нужно удалить из множества т.и т.т., когда она наша новая прямая пересекает ее в точке с координатой по оси X, меньшей, чем последняя - предпоследнюю.

Доказательство : Пусть [math]Y(x) = Kx + B[/math] - уравнение новой прямой, [math]y[i](x) = K[i]x + B[i][/math] - уравнения прямых множества. Тогда т.к. [math]K \lt K[sz][/math], то при [math]x \in [- \infty; xR] : y[sz](x) \lt = Y(x)[/math], а т.к. [math] K[sz] \lt K[sz - 1][/math], то при [math]x \in [xL; + \infty] : y[sz - 1](x) \gt = y[sz](x)[/math]. Если [math]xL \lt xR[/math], то при [math]x \in [xL; xR] : y[sz - 1] \gt = y[sz](x) и Y(x) \gt = y[sz](x)[/math], т.е. на отрезке [math][xL; xR][/math] прямая номер sz лежит ниже остальных и её нужно оставить в множестве. Если же [math]xL \gt xR[/math], то она ниже всех на отрезке [math][xL; xR] = \varnothing [/math], т.е. её можно удалить из множества

Детали реализации:

Будем хранить 2 массива : [math]front[][/math] - [math]x[/math]-координаты, начиная с которых прямые совпадают с выпуклой оболочкой (т.е. i-я прямая совпадает с выпуклой оболочкой текущего множества прямых при [math]x[/math] [math]\in[/math] [math][front[i]; front[i + 1])[/math] ) и [math]st[][/math] - номера деревьев, соответствующих прямым (т.е. [math]i[/math]-я прямая множества, где [math]i[/math] [math]\in[/math] [math][1; sz][/math] соответствует дереву номер [math]sz[i][/math]). Также воспользуемся тем, что [math]x[i] = a[i][/math] возрастают (по условию задачи), а значит мы можем искать первое такое [math]j[/math], что [math]x[i] \gt = front[j][/math] не бинарным поиском, а методом двух указателей за [math]O(n)[/math] операций суммарно. Также массив front[] можно хранить в целых числах, округляя х-координаты в сторону лежащих правее по оси x до ближайшего целого (*), т.к. на самом деле мы, считая динамику, подставляем в уравнения прямых только целые [math]x[i][/math], а значит если [math]k[/math]-я прямая пересекается с [math]k+1[/math]-й в точке [math]z +[/math] [math]\alpha[/math] (z-целое, [math]\alpha[/math] [math]\in[/math] [math][0;1)[/math]), то мы будем подставлять в их уравнения [math]z[/math] или [math]z + 1[/math]. Поэтому можно считать, что новая прямая начинает совпадать с выпуклой оболочкой, начиная с [math]x = z+1[/math]

Реализация

 void Convex-hull-trick
 st[1] = 1
 from[1] = -[math]\infty[/math]// первая прямая покрывает все x-ы, начиная с -∞ 
 sz = 1 // текущий размер выпуклой оболочки 
 pos = 1 // текущая позиция первого такого j, что x[i] >= front[st[j]] 
 for  i = 2..n  {
      while (front[pos] < x[i]) // метод 1 указателя (ищем первое pos, такое что x[i] покрывается "областью действия" st[pos]-той прямой 
           pos = pos + 1
      j = st[pos]
      dp[i] = K[j] * a[i] + B[j] 
      if (i < n) {  // если у нас добавляется НЕ последняя прямая, то придется пересчитать выпуклую оболочку 
            K[i] = c[i]  // наши переобозначения переменных 
            B[i] = dp[i] // наши переобозначения переменных 
            x = -[math]\infty[/math] 
            while (true) {
                  j = st[sz]
                  x = divide(B[j] - B[i], K[i] - K[j]) // x-координата пересечения с последней прямой оболочки, округленное в нужную сторону (*) 
                  if (x > from[sz]) break  // перестаем удалять последнюю прямую из множества, если новая прямая пересекает ее позже, чем начинается ее "область действия" 
                  sz = sz - 1// удаляем последнюю прямую, если она лишняя 
             }
             st[sz + 1] = i  
             from[sz + 1] = x // добавили новую прямую 
             sz = sz + 1
      }                       
 }          

Здесь функция divide(a, b) возвращает нужное(*) округление a / b. Приведем её код :

int divide (a, b)
       delta = 0
       if (a mod b ≠ 0) delta = 1
       if ((a > 0 and b > 0) or (a < 0 and b < 0)) return [a / b] + delta
       return -[|a| / |b|]

Такая реализация будет работать за O(n).

Динамический convex hull trick

Заметим, что условия на прямые, что [math]k[i][/math] возрастает/убывает и [math]x[i][/math] убывает/возрастает выглядят достаточно редкими для большинства задач. Пусть в задаче таких ограничений нет. Первый способ борьбы с этой проблемой - отсортировать входные данные нужным образом, не испортив свойств задачи (пример : задача G отсюда http://neerc.ifmo.ru/school/camp-2016/problems/20160318a.pdf).

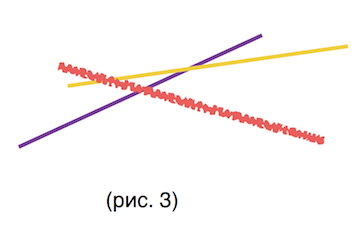
Но рассмотрим общий случай. По-прежнему у нас есть выпуклая оболочка прямых, имея которую мы за [math]O(logn)[/math] можем найти [math]dp[i][/math], но теперь вставку [math]i[/math]-й прямой в оболочку уже нельзя выполнить описанным ранее способом за [math]O(1)[/math] в среднем. У нас есть выпуклая оболочка, наша прямая пересекает ее, возможно, «отсекая» несколько отрезков выпуклой оболочки в середине (рис. 4 : красная прямая - та, которую мы хотим вставить в наше множество). Более формально : теперь наша новая прямая будет ниже остальных при [math]x \in [x1; x2][/math], где [math]x1, x2 \in R[/math] - точки пересечения с некоторыми прямыми, причем [math]x2[/math] не обязательно равно [math]+ \infty[/math]

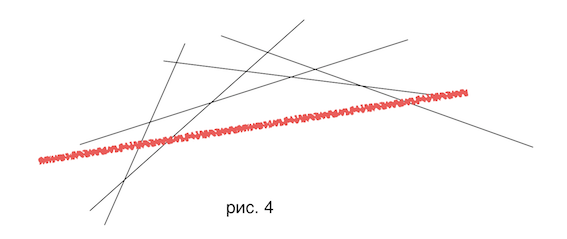
Чтобы уметь вставлять прямую в множество будем хранить [math]std::set[/math] (или любой аналог в других языках программирования) пар [math](k, st)[/math] = [math](коэффицент прямой, ее номер в глобальной нумерации)[/math]. Когда приходит новая прямая, ищем последнюю прямую с меньшим угловым коэффицентом, чем у той прямой, которую мы хотим добавить в множество. Поиск такой прямой занимает [math]O(log(n))[/math]. Начиная с найденной прямой выполняем "старый" алгоритм (удаляем, пока текущая прямая множества бесполезна). И симметричный алгоритм применяем ко всем прямым справа от нашей (удаляем правого соседа нашей прямой, пока она пересекает нас позже, чем своего правого соседа).

Асимптотика решения составит [math]O(logn)[/math] на каждый из [math]n[/math] запросов «добавить прямую» + [math]O(n * log(n))[/math] суммарно на удаление прямых, т.к. по-прежнему каждая прямая не более одного раза удалится из множества, а каждое удаление из std::set занимает [math]O(log(n))[/math] времени. Итого [math]O(nlogn)[/math].

Альтернативный подход

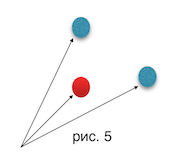
Другой способ интерпретировать выражение [math]dp[i] = \min_{j=0...i-1}(c[j]*a[i] + dp[j])[/math] заключается в том, что мы будем пытаться свести задачу к стандартной выпуклой оболочке множества точек. Перепишем выражение средующим образом : [math]dp[j] + a[i] * c[j] = (dp[j], c[j]) * (1, a[i])[/math], т.е. запишем как скалярное произведение векторов [math]v[j] = (dp[j], c[j])[/math] и [math]u[i] = (1, a[i])[/math]. Вектора [math]v[j] = (dp[j], c[j])[/math] хотелось бы организовать так, чтобы за [math]O(logn)[/math] находить вектор, максимизирующий выражение [math]v[j] * u[i][/math]. Посмотрим на рис. 5. Заметим интуитивно очевидный факт : красная точка (вектор) [math]j[/math] не может давать более оптимальное значение [math]v[j] * u[i][/math] одновременно чем обе синие точки. По этой причине нам достаточно оставить выпуклую оболочку векторов [math]v[j][/math], а ответ на запрос - это поиск [math]v[j][/math], максимизирующего проекцию на [math]u[i][/math]. Это задача поиска ближайшей точки выпуклого многоугольника (составленного из точек выпуклой оболочки) к заданной прямой (из [math](0, 0)[/math](1, a[i])</tex>). Ее можно решить за [math]O(logn)[/math] двумя бинарными или одним тернарным поиском Асимптотика алгоритма по-прежнему составит [math]O(nlog(n))[/math]

Доказательство : необходимо показать, что если есть 3 вектора a, b, c, расположенные как на рисунке 5 (т.е. [math][a-b, b-c] \leqslant 0[/math], где [math][u, v][/math] - модуль векторного произведения векторов [math]u[/math] и [math]v[/math]), то либо (a, u[i]) \leqslant (b, u[i]), либо (c, u[i]) \leqslant (b, u[i]).

Распишем условие того, что точка b не лежит на выпуклой оболочке векторов [math]0, a, b, c [/math] : [math][a-b, b-c] \leqslant 0 \Leftrightarrow (a_{x} - b_{x})\cdot(b_{y} - c_{y}) \leqslant (a_{y} - b_{y}) \cdot (b_{x} - c_{x})[/math] (*). Предположим (от противного), что [math](b, u[i]) \leqslant (a, u[i]) \Leftrightarrow b_{x} + a[i] \cdot b_{y} \leqslant c_{x} + a[i] \cdot c_{y} \Leftrightarrow (b_{x} - c_{x}) \leqslant a[i] \cdot (c_{y} - b_{y})[/math] и [math](b, u[i]) \leqslant (c, u[i]) \Leftrightarrow b_{x} + a[i] \cdot b_{y} \leqslant a_{x} + a[i] \cdot a_{y} \Leftrightarrow (a_{x} - b_{x}) \geqslant a[i] \cdot (b_{y} - a_{y})[/math].

Подставим эти неравенства в (*). Получим цепочку неравенств : [math]a[i] \cdot (a_{y} - b_{y})[/math][math] \cdot (c_{y} - b_{y}) = a[i][/math][math] \cdot (b_{y} - a_{y}) \cdot [/math][math](b_{y} - c_{y})[/math] [math]\leqslant (a_{x} - b_{x})[/math][math] \cdot (b_{y} - c_{y})[/math][math] \leqslant (a_{y} - b_{y}) \cdot [/math][math](b_{x} - c_{x})[/math] [math]\leqslant a[i] \cdot (a_{y} - b_{y})[/math][math] \cdot (c_{y} - b_{y})[/math]. Получили противоречие : [math]a[i] \cdot (a_{y} - b_{y}) \cdot (c_{y} - b_{y}) \leqslant a[i] \cdot (a_{y} - b_{y}) \cdot (c_{y} - b_{y})[/math]. Значит предположение неверно, чтд.