Факторизация графов

Определение:

Фактором (англ. factor) графа [math]G[/math] называется остовный подграф графа [math]G[/math], имеющий хотя бы одно ребро.

Определение:

Граф [math]G[/math] — сумма факторов [math]G_i[/math], если графы [math]G_i[/math] не имеют попарно общих рёбер, а [math]G[/math] является их объединением. Такое разложение называется факторизацией (англ. factorization) графа [math]G[/math].

Определение:

[math]n[/math]-фактор — регулярный остовный подграф степени [math]n[/math]. Если граф [math]G[/math] представляет собой сумму [math]n[/math]-факторов, то их объединение называется [math]n[/math]-факторизацией, а сам граф [math]G[/math] назыается [math]n[/math]-факторизуемым.

1-факторизация

Теорема:

Полный граф [math]K_{2n}[/math] [math]1[/math]-факторизуем.

Доказательство:

[math]\triangleright[/math]

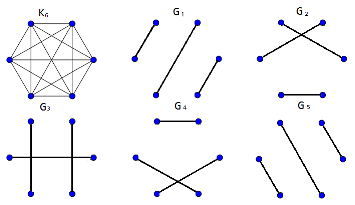
[math]1[/math]-факторизация графа [math]K_6[/math] Нам нужно только указать разбиение множества рёбер [math]E[/math] графа на [math](2n - 1)[/math] [math]1[/math]-фактора. Для этого обозначим вершины графа [math]G[/math] через [math]v_1, v_2, \dots, v_{2n}[/math] и определим множества рёбер [math]X_i = (v_iv_{2n}) \cup (v_{i - j}v_{i + j}; j = 1, 2, \dots, n - 1)[/math], [math]i = 1, 2, \dots, 2n - 1 [/math], где каждый из индексов [math]i - j[/math] и [math]i + j[/math] является одним из чисел [math]1, 2, \dots, 2n - 1[/math]; здесь сумма и разность берутся по модулю [math]2n - 1[/math]. Легко видеть, что набор [math]X_i[/math] даёт необходимое разбиение множества [math]X[/math], а сумма подграфов [math]G_i[/math], порождённых множествами [math]X_i[/math], является [math]1[/math]-факторизацией графа [math]K_{2n}[/math].

[math]\triangleleft[/math]

2-факторизация

Утверждение:

Если граф [math]2[/math]-факторизуем, то каждый его фактор должен быть объединением непересекающихся (по вершинам) циклов.

[math]\triangleright[/math]

Начнём обход [math]2[/math]-фактора с какой-то вершины. Пойдём по одному из её рёбер и попадаем в смежную ей вершину. Далее идём по рёбрам, по которым мы ещё не ходили. Мы входим в вершину по одному ребру и выходим по другому, так как степень каждой вершины равна [math]2[/math], пока не вернёмся в первую вершину. Это цикл, так как в каждой вершине мы были только один раз. Если есть вершины, которые мы не посетили, то снова начинаем обход с любой из таких вершин. В вершины прежних циклов попасть нельзя, так как мы уже проходили по рёбрам этих вершин. Значит, циклы не пересекаются по вершинам.

[math]\triangleleft[/math]

Теорема (J. Petersen, 1981, О наличии [math]2[/math]-фактора в регулярном графе чётной степени.):

Пусть [math]G[/math]—регулярный граф чётной степени. Тогда в [math]G[/math] есть [math]2[/math]-фактор.

Доказательство:

[math]\triangleright[/math]

coming soon

[math]\triangleleft[/math]

Заметим, что если [math]2[/math]-фактор связен, то он является гамильтоновым циклом.

Теорема:

Граф [math]K_{2n+1}[/math] можно представить в виде суммы [math]n[/math] гамильтоновых циклов.

Доказательство:

[math]\triangleright[/math]

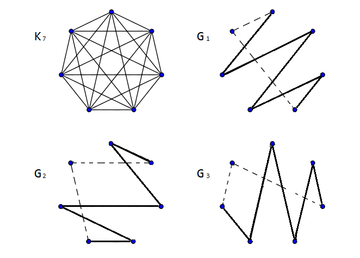[math]2[/math]-факторизация графа [math]K_7[/math]. Рёбра, отмеченные пунктиром, не пересекают другие рёбра при правильной укладке графа. Для того чтобы в графе [math]K_{2n+1}[/math] построить [math]n[/math] гамильтоновых циклов, непересекающихся по рёбрам, перенумеруем сначала его вершины [math]v_1, v_2, \dots, v_{2n+1}[/math]. На множестве вершин [math]v_1, v_2, \dots, v_{2n}[/math] зададим [math]n[/math] непересекающихся простых цепей [math]P_i=v_i v_{i-1} v_{i+1} v_{i-2} \dots v_{i+n-1}v_{i-n}[/math] следующим образом: [math]j[/math]-ой вершине цепи [math]P_i[/math] является вершина [math]v_k[/math], где [math]k=i+(-1)^{j+1}\dfrac{j}{2}[/math], все индексы приводятся к числам [math]1, 2, \dots, 2n [/math] по модулю [math]2n[/math]. Гамильтонов цикл [math]Z_i[/math] можно получить, соединив вершину [math]v_{2n+1}[/math] с концевыми вершинами цепи [math]P_i[/math].

[math]\triangleleft[/math]

Замечания

• Факторизация графов используется как один из способов построения покрывающих наборов, используемых при создании тестов для программ с большим количеством параметров.
• [math]1[/math]-факторизация [math]k[/math]-регулярного графа является рёберной [math]k[/math]-раскраской графа.

См. также

• Гамильтоновы графы
• Остовные деревья
• Основные определения теории графов

Источники информации

• Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
• Wikipedia — Graph factorization