Неравенство Крафта

Рассматриваемое ниже неравенство Крафта показывает для каких длин кодовых слов существует префиксный код.

Теорема (неравенство Крафта):

Пусть [math]\Sigma[/math] — алфавит из [math]n[/math] символов, кодовые слова которого имеют длины [math]l_1 \leqslant l_2 \leqslant \ldots \leqslant l_n [/math]. Тогда необходимое и достаточное условие существования префиксного кода в [math]r[/math]-ичном алфавите для символов из [math]\Sigma[/math], состоит в выполнении неравенства: [math] \sum\limits_{i = 1}^{n} r ^{-l_i} \leqslant 1 [/math]

Доказательство:

[math]\triangleright[/math]

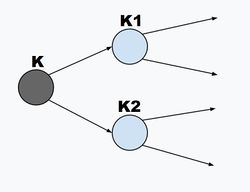
Иллюстрация к доказательству индукционного перехода Необходимость: Напомним, что префиксный код можно представить в виде [math]r[/math]-ичного корневого дерева, рёбра которого соответствуют символам алфавита, а листья соответствующим кодам. Неравенство Крафта будем доказывать по индукции. Для простоты рассмотрим сначала случай двоичного алфавита, то есть [math]r = 2[/math]. База: Если максимальная длина пути на дереве равна [math]1[/math], то в дереве есть одно или два ребра длины [math]1[/math]. Таким образом, либо [math] \dfrac{1}{2} \leqslant 1 [/math] — для одного символа источника, либо [math] \dfrac{1}{2} + \dfrac{1}{2} \leqslant 1 [/math] — для двух символов источника. Переход: Предположим далее, что неравенство Крафта справедливо для всех деревьев высоты меньше [math]n - 1[/math]. Докажем, что оно справедливо и для всех деревьев высоты меньше [math]n[/math]. Для данного дерева максимальной высоты [math]n[/math] ребра из первой вершины ведут к двум поддеревьям, высоты которых не превышают [math]n - 1[/math]; для этих поддеревьев имеем неравенства [math]K_1 \leqslant 1[/math] и [math]K_2 \leqslant 1[/math], где [math]K_1, K_2[/math] — значения соответствующих им сумм. Каждая длина [math]l_i[/math] в поддереве увеличивается на [math]1[/math], когда поддерево присоединяется к основному дереву, поэтому возникает дополнительный множитель [math]\dfrac{1}{2}[/math]. Таким образом, имеем [math]\dfrac{1}{2} K_1 + \dfrac{1}{2} K_2 \leqslant 1[/math]. В случае произвольного недвоичного основания [math]r[/math] имеется не более [math]r[/math] ребер, исходящих из каждой вершины, то есть не более [math]r[/math] поддеревьев; каждое из них присоединяется к основному дереву, давая дополнительный множитель [math]\dfrac{1}{r}[/math]. Отсюда снова следует утверждение теоремы. Достаточность: Если некоторое [math] l_i = 0 [/math] , то [math] n = 1 [/math] . В таком случае пустая строка является искомым префиксным кодом. Далее все [math] l_i \geqslant 1 [/math] . Пусть у нас есть [math]n[/math] символов, кодовые слова которого имеют длины [math]l_1 \leqslant l_2 \leqslant \ldots \leqslant l_n [/math]. Давайте разделим данные символы на [math]r[/math] групп, внутри каждой из которых [math] \sum\limits r ^{-l_i} \leqslant \dfrac{1}{r} [/math] . Разделить символы на группы можно следующим жадным образом: брать [math] l_i [/math] в порядке увеличения индекса. Докажем, что в таком случае группа будет либо полностью укомплектована, либо будут исчерпаны все возможные [math] l_i [/math] . Это следует из того, что при [math] l_i \geqslant 1 [/math] на [math]i[/math]-ом шаге либо группа уже укомплектована, либо ее остаток равен: [math] \dfrac{1}{r} - \left ( \dfrac{1}{r^{l_1}} + \ldots + \dfrac{1}{r^{l_i-1}} \right ) = \dfrac{r^{l_{i-1}} - ( r^{l_i - l_1} + r^{l_i - l_2} + \ldots + r^{l_i - l_{i - 1}} )}{r^{l_i}}[/math] Так как группа не укомплектована, то числитель положителен. Если добавим [math] l_i [/math] в группу, то числитель уменьшится на [math]1[/math]. Тогда, взяв [math] l_i [/math] в группу, мы не перепрыгнем через максимальное значение. А значит, создавая группы по данному алгоритму мы сможем построить [math]r[/math] групп, удовлетворяющих условию. Для доказательства достаточности опишем рекурсивную процедуру, которая строит код для данного набора длин [math] l_i [/math] , удовлетворяющих неравенству [math] \sum\limits_{i = 1}^{n} r ^{-l_i} \leqslant 1 [/math] . Разделим длины [math] l_i [/math] на [math]r[/math] групп, внутри каждой из которых [math] \sum\limits r ^{-l_i} \leqslant \dfrac{1}{r} [/math] . Разделить длины на группы будем алгоритмом описанным выше. У всех слов из одной группы будет одна и та же начальная буква. Запуститим данную процедуру для каждой группы слов, предварительно обрезав первую букву. Доказательство корректности проведём по индукции по величине [math] l_n [/math] . База: Если [math] l_n = 0 [/math], то процедура корректна. Переход: Допустим, что процедура корректна для [math] l_n = w [/math] . Докажем, что процедура корректна и для [math] l_n = w + 1 [/math] . Заметим, что у слов каждой группы будет своя начальная буква, поэтому достаточно проверить префиксность кода для каждой группы. А это истинно по предположению индукции, где для каждой группы [math] l_i \leqslant w [/math] .

[math]\triangleleft[/math]

Замечания

Когда имеет место строгое неравенство? Легко заметить, что если любая концевая вершина дерева является кодовым словом, то [math]K = 1[/math]. Строгое неравенство имеет место лишь в случае, когда некоторые из концевых вершин не используются. Однако, в случае двоичного кодового алфавита какая-нибудь концевая вершина не используется, то предыдущее решение оказывается лишним, и соответствующая цифра может быть удалена из каждого кодового слова, декодирование которого проходит через эту вершину. Таким образом, если имеет место строгое неравенство, то код неэффективен, но для двоичных деревьев очевидно, как можно его улучшить.

Заметим еще раз, что теорема утверждает существование такого кода и ничего не говорит о конкретных кодах. Может существовать код, который удовлетворяет неравенству Крафта и тем не менее не является префиксным.

См.также

• Неравенство Макмиллана

Источники информации

• Википедия — Неравенство Крафта
• Неравенство Крафта
• Kraft's inequality