Задача о динамической связности

Задача:

Есть неориентированный граф из [math]n[/math] вершин, изначально не содержащий рёбер. Требуется обработать [math]m[/math] запросов трёх типов: [math]\mathrm{add(u,v)}[/math] — добавить ребро между вершинами [math]u[/math] и [math]v[/math]; [math]\mathrm{remove(u,v)}[/math] — удалить ребро между вершинами [math]u[/math] и [math]v[/math]; [math]\mathrm{connected(u,v)}[/math] — проверить, лежат ли вершины [math]u[/math] и [math]v[/math] в одной компоненте связности.

Динамическая связность в лесах

Если задача такова, что в графе нет и не может быть циклов, то она сводится к задаче о связности в деревьях эйлерова обхода. Время работы каждого запроса для упрощённой задачи — [math]O(\log n)[/math].

Обобщение задачи для произвольных графов

Существуют задачи, в которых граф не обязательно на протяжении нашей работы после каждой операции добавления ребра остаётся лесом. Добавление рёбер можно рассмотреть с точки зрения системы непересекающихся множеств, такой запрос будет работать за [math]O(\mathrm{\log}n)[/math]. Операция проверки сводится к проверке связности в остовном лесе и работает также за [math]O(\mathrm{\log}n)[/math].

Попробуем выполнить операцию удаления ребра. Для этого в каждой компоненте связности выделим остовные деревья, которые образуют остовный лес. Граф и его остовный лес — одно и то же с точки зрения связности.

Произвольный граф

Остовный лес в графе

Введём функцию [math]l(e):e{\rightarrow}[0;\mathrm{\log} n][/math] и назовём её уровнем ребра [math]e[/math]. Будем рассматривать графы [math]G_i=\langle V, E\rangle: \{E | l(E) \geqslant i\}[/math]. Очевидно, что [math]G_{\mathrm{\log}n} \subseteq G_{\mathrm{\log}n-1} \subseteq \ldots \subseteq G_1 \subseteq G_0[/math]. Выделим в них остовные леса таким образом, что [math]F_{\mathrm{\log}n} \subseteq F_{\mathrm{\log}n-1} \subseteq ... \subseteq F_1 \subseteq F_0[/math], где [math]F_i[/math] — остовный лес графа [math]G_i[/math].

При удалении возможны случаи:

• Удаляемое ребро является мостом. В этом случае дерево распадается на две части (назовём их [math]T(u)[/math] и [math]T(v)[/math]), и задача решается как для дерева за [math]O(\mathrm{\log}n)[/math].
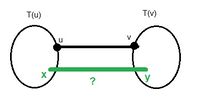
• Удаляемое ребро не является мостом. Тогда существует другое ребро, соединяющее две части исходной компоненты (под частями подразумевается какое-то разбиение множества вершин на два, при этом вершины [math]u[/math] и [math]v[/math] лежат в разных частях. Если [math]uv[/math] принадлежало нашему лесу, то передаём эту "функцию" новому ребру.

Осталось проверить, является ли ребро мостом. Будем искать ребро [math]xy[/math] на уровне [math]l(uv)[/math], затем [math]l(uv)-1[/math], [math]l(uv)-2[/math][math]{{...}}[/math]. Рассматривать будем меньшую из частей (будем считать, что [math]|T(u)|\leqslant|T(v)|[/math], в противном случае просто поменяем исследуемые вершины местами). Если мы находим такое ребро, что оно ведёт в другую часть, то останавливаемся и говорим, что [math]uv[/math] не мост. Иначе увеличиваем уровень ребра, чтобы заново к нему не обращаться или уменьшаем уровень и повторяем процедуру. Суммарная сложность сканирования рёбер будет [math]O(|T(u)|\mathrm{\log}n)[/math], так как в худшем случае мы проверяем каждую вершину из [math]T(u)[/math], а уровень ребра не превосходит [math]\mathrm{\log}n[/math].

Общее время удаления одного ребра не превосходит [math]O(\mathrm{\log}^2{n}+S\cdot\mathrm{\log}n)[/math], где [math]S[/math] — число неудачных просмотров ребра [math]xy[/math], а для всех [math]m[/math] запросов получаем [math]O(\mathrm{\log}^2{n}\cdot m+\mathrm{\log}n\cdot\sum{S}) \leqslant O(\mathrm{\log}^2{n} \cdot m+\mathrm{\log}n\cdot\mathrm{\log}n\cdot m) = O(2\cdot\mathrm{\log}^2{n}\cdot m)[/math], поэтому для одного запроса будем иметь время [math]O(\mathrm{\log}^2{n})[/math].

См. также

• Деревья эйлерова обхода
• Задача о динамической связности оффлайн

Источники информации

• Dynamic connectivity — Википедия
• Лекции — Академия Яндекса