Задача о динамической связности — различия между версиями
(→remove(u,v)) |
(→remove(u,v)) |
||
| Строка 55: | Строка 55: | ||
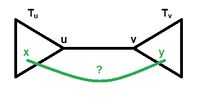
Проверим, является ли ребро. У ребра <tex>uv</tex> известен уровень, пусть он равен <tex>i</tex>. Попробуем найти другое ребро (<tex>xy</tex>), соединяющее поддеревья <tex>T_u</tex> и <tex>T_v</tex>, на которые распалось остовное дерево исследуемой компоненты. | Проверим, является ли ребро. У ребра <tex>uv</tex> известен уровень, пусть он равен <tex>i</tex>. Попробуем найти другое ребро (<tex>xy</tex>), соединяющее поддеревья <tex>T_u</tex> и <tex>T_v</tex>, на которые распалось остовное дерево исследуемой компоненты. | ||
| − | + | ||
<!----При удалении возможны случаи: | <!----При удалении возможны случаи: | ||
Версия 22:08, 14 января 2018
| Задача: |
Есть неориентированный граф из вершин, изначально не содержащий рёбер. Требуется обработать запросов трёх типов:
|
Содержание
Динамическая связность в лесах
Если задача такова, что в графе нет и не может быть циклов, то она сводится к задаче о связности в деревьях эйлерова обхода. Время работы каждого запроса для упрощённой задачи — .
Обобщение задачи для произвольных графов
Существуют задачи, в которых граф не обязательно на протяжении нашей работы после каждой операции добавления ребра остаётся лесом. Для решения таких задач в каждой компоненте связности выделим остовные деревья, которые образуют остовный лес. Попробуем выполнить операцию удаления ребра.--- Для этого ---->
connected(u,v)
Граф и его остовный лес — одно и то же с точки зрения связности. Поэтому проверка связности в графе сводится к проверке связности в остовном лесе и решается за .
add(u,v)
Чтобы разобраться с тем, как изменится граф и остовный лес при добавлении и удалении ребра, введём функцию и назовём её уровнем ребра . Уровни ребра можно распределить любым способом, но для всех должно выполняться следующее свойство: размер каждой компоненты связности не превосходит . Здесь графы определяются так: .
Очевидно, что . Выделим в графах остовные леса таким образом, что , где — остовный лес графа .
Удобнее всего новому ребру давать уровень . В этом случае изменится только , так как в остальные подграфы рёбра нулевого уровня не входят. После вставки нового ребра нам нужно проверить, были ли вершины и в одной компоненте связности до того, как мы вставили ребро. Если они лежали в разных компонентах, то необходимо новое ребро добавить и в остовный лес .
remove(u,v)
| Утверждение: |
Если ребро, которое мы хотим удалить, не принадлежит остовному лесу, то связность между любой парой вершин сохранится. |
|
Допустим, что это не так. Понятно, что при разрезании ребра нового пути между вершинами не появится. Предположим, что нарушилась связность для каких-то двух вершин. Значит, мы убрали мост. А любой мост принадлежит всем остовным деревьям его компоненты. Противоречие. |
Таким образом, если мы удалили ребро не из остовного леса, то нам не придётся перестраивать лес и пересчитывать значение . Рассмотрим случаи, когда мы берём ребро из леса. Тогда необходимо выяснить, не является ли данное ребро мостом в графе, и выполнить соответствующие действия.
Проверим, является ли ребро. У ребра известен уровень, пусть он равен . Попробуем найти другое ребро (), соединяющее поддеревья и , на которые распалось остовное дерево исследуемой компоненты.