Теорема о декомпозиционном барьере — различия между версиями
Leugenea (обсуждение | вклад) |
|||
| Строка 6: | Строка 6: | ||
|proof= | |proof= | ||
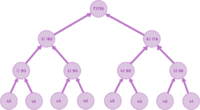
[[Файл:example.png|200px|thumb|right|Пример для <tex>V = 16</tex>, в который надо добавить нужное количество ребер]] | [[Файл:example.png|200px|thumb|right|Пример для <tex>V = 16</tex>, в который надо добавить нужное количество ребер]] | ||
| − | <div>Используются <tex>c_{1} = | + | <div>Используются <tex>c_{1} = \frac{11}{10}</tex> и <tex>c_{2} = \frac{1}{9}</tex> ( <tex>\frac{11}{10} V \le E \le \frac{V^2}{9}</tex>). Чтобы получить искомую сеть, строится сеть, изображенный на рисунке, после чего добавляется нужное количество ребер из <tex>A</tex> в <tex>B</tex> (а именно, <tex>E-V+1</tex> ребро). Пропускные способности ребер из <tex>A</tex> в <tex>B</tex> равны <tex>1</tex>, остальных — <tex>+\infty</tex> (или просто достаточно большое число, например, <tex>V^2</tex>).</div> |
Теперь докажем саму теорему: | Теперь докажем саму теорему: | ||
* Максимальный поток по модулю равен потоку через разрез, который разделяет <tex>A</tex> и <tex>B</tex> (т.е. пересекает все ребра с пропускной способностью <tex>1</tex>). Поток по каждому пути в декомпозиции не превышает 1, а значит, этих путей не меньше, чем ребер между <tex>A</tex> и <tex>B</tex>, а их <tex>\Omega (E)</tex>. | * Максимальный поток по модулю равен потоку через разрез, который разделяет <tex>A</tex> и <tex>B</tex> (т.е. пересекает все ребра с пропускной способностью <tex>1</tex>). Поток по каждому пути в декомпозиции не превышает 1, а значит, этих путей не меньше, чем ребер между <tex>A</tex> и <tex>B</tex>, а их <tex>\Omega (E)</tex>. | ||
| − | * По построению сети, любой путь из <tex>s</tex> в <tex>t</tex> содержит хотя бы <tex>( | + | * По построению сети, любой путь из <tex>s</tex> в <tex>t</tex> содержит хотя бы <tex>(V-2[\frac{V-1}{3}]+1)</tex> ребер, что является <tex>\Omega (V)</tex>. |
}} | }} | ||
Версия 09:24, 29 декабря 2010
| Теорема (о декомпозиционном барьере): |
Существуют положительные вещественные числа и , такие что для любых натуральных и , удовлетворяющих неравенствам , существует сеть с вершинами и ребрами. При этом для любого максимального потока в , любая его остаточная декомпозиция должна содержать слагаемых (т.е. путей или циклов), причем каждый из путей (циклов) в декомпозиции должен иметь длину . |
| Доказательство: |
|
Используются и ( ). Чтобы получить искомую сеть, строится сеть, изображенный на рисунке, после чего добавляется нужное количество ребер из в (а именно, ребро). Пропускные способности ребер из в равны , остальных — (или просто достаточно большое число, например, ).
Теперь докажем саму теорему:
|